python中最全面的统计分布工具-Toy模板网

这篇具有很好参考价值的文章主要介绍了python中最全面的统计分布工具。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

正态分布

scipy为诸多统计分布函数设计了类，这些类封装了几乎相同的方法，下面先以正态分布为示例，预览一下强大的统计功能。

import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt

rv = norm()

# 绘制正态分布的概率密度曲线
x = np.linspace(-3, 3, 100)
plt.plot(x, rv.pdf(x), 'k-', lw=2, label='frozen pdf')

# 生成1000个随机数，并绘制直方图
r = norm.rvs(size=1000)
plt.hist(r, density=True, bins='auto', alpha=0.2)

# 将norm.pdf当作静态方法调用
plt.plot(x, norm.pdf(x),
    'r-', lw=1, alpha=0.6, label='norm pdf')

plt.legend()
plt.xlim(-3,3)
plt.show()

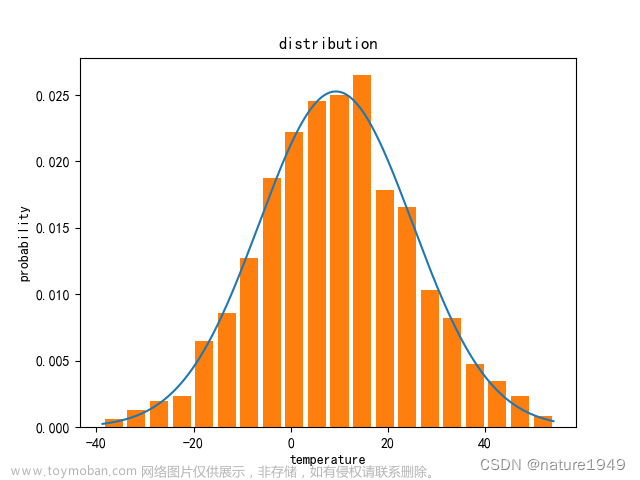
结果如图所示

python中最全面的统计分布工具

其中，norm为正态分布类，rv是正态分布对象，然后调用rv.pdf函数，绘制出rv这个标准正态分布的概率密度函数曲线。

接下来通过rvs函数，创建了1000个随机数，并通过hist函数将其直方图画出，可以看到，这个直方图的分布情况，与概率密度函数所刻画的范围是相对一致的。

最后，直接调用norm的静态方法.pdf，得到了与rv.pdf相同的输出结果。

这就是scipy.stats中封装的概率类的基本使用方法，下面对这些类做一个统一的介绍。

属性和方法

作为概率类，其最重要的功能就是生成随机数，通过调用.rvs方法，可以生成任意维度的随机数，其定义如下

rvs(loc=0, scale=1, size=1, random_state=None)  # 连续型
rvs(p, loc=0, size=1, random_state=None)        # 离散型

其中，loc和scale用于尺度放缩，size为生成随机数的维度，random_state为随机数种子，指定后便于结果复现。

对于分布函数、概率密度函数等分布的基本特征，这些类除了提供原始函数外，还提供了对数函数，这些函数的输入参数均为(k, a, n, loc=0)

原始函数	对数函数	说明
pmf	logpmf	概率质量函数，适用于离散型
pdf	logpdf	概率密度函数，适用于连续型
cdf	logcdf	累加分布函数
ppf		百分点函数(cdf的反函数)
sf	logsf	残差函数 (1 - cdf)
isf		残差函数的反函数

概率类提供了一些最常用的统计量函数，离散分布的参数均为(a, n, loc=0)，连续分布的参数均为(loc=0, scale=1)。

中位数	均值	方差	标准差	熵
`median`	`mean`	`var`	`std`	`entropy`

另外，还提供了一个统一的函数stats(a, n, loc=0, moments=’mv’)，可以一次性输出这些统计量。其moments的标准字符为：Mean(‘m’), variance(‘v’), skew(‘s’) orkurtosis(‘k’)。

通过interval函数，可以求取分布的置信区间，其输入参数如下，confidence为置信水平。

interval(confidence, loc=0, scale=1)    # 连续型
interval(confidence, p, loc=0)          # 离散型

通过expect函数可以计算概率分布的期望，其输入参数为

expect(func, args=(), loc=0, scale=1, lb=None, ub=None, conditional=False, **kwds)  # 连续型
expect(func, args=(p,), loc=0, lb=None, ub=None, conditional=False) # 离散型

其中，func为作用在概率分布之上的函数，lb, ub表示求期望的区间。

测试

下面仍然基于正态分布，对一些函数进行简单的测试

>>> rv.interval(0.5)
(-0.6744897501960817, 0.6744897501960817)
>>> rv.interval(0.5, loc=2)
(1.3255102498039184, 2.6744897501960816)
>>> rv.interval(0.5, scale=2)
(-1.3489795003921634, 1.3489795003921634)

上面代码测试了置信区间函数，第一行表示在(-0.6744897501960817, 0.6744897501960817)区间内发生的概率为 $50\%$ 。

在指明loc参数为2后，整个结果向右平移了2；指明scale为2后，概率分布函数被拉平了，从而置信区间也跟着乘以2。

>>> rv.expect()
0.0
>>> rv.expect(lb=-1, ub=2)
0.18797975800595532
>>> rv.expect(lb=-1, ub=3)
0.2375388761072053
>>> rv.expect(lb=-1, ub=4)
0.24183689429337848