三轴陀螺仪解算姿态（四元数）-Toy模板网

这篇具有很好参考价值的文章主要介绍了三轴陀螺仪解算姿态（四元数）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

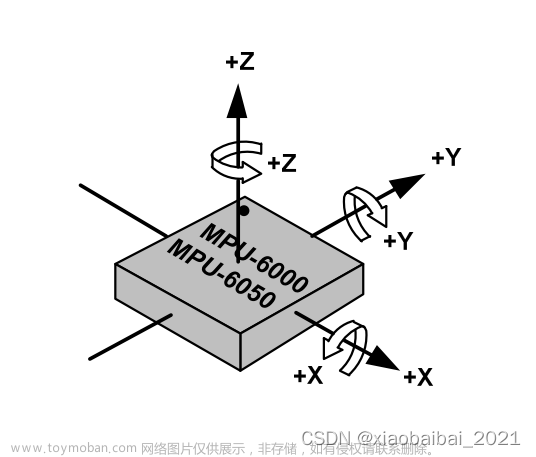
原理

三轴陀螺仪可以测量载体在三个轴上的角速度分量，对这些角速度进行积分就可以得到旋转的角度，应用到载体上就可以得到载体的姿态。

方法

假设导航坐标系为东北天，载体坐标系为右前上。

初始载体坐标系和导航坐标系重合，对应的四元数为q=[1,0,0,0]，使用此四元数表示载体在导航坐标系下的旋转。

三轴陀螺仪测量的三个角速度分量可以合成一个角速度向量，可以理解为载体绕着这个角速度向量进行旋转，旋转的角度为角速度向量模的积分。

设 $\overrightarrow{gyro}=\begin{bmatrix} \omega_{xb} \\ \omega_{yb} \\ \omega_{zb} \end{bmatrix}$ 为陀螺仪测得的载体旋转的角速度向量，时间间隔为 $d t$ ，则旋转向量为

$\overrightarrow{\omega_{b}} =\begin{bmatrix} \omega_{xb} \\ \omega_{yb} \\ \omega_{zb} \end{bmatrix} \cdot dt$

将其转换到导航坐标系
$\overrightarrow{\omega_{n}}=q\otimes\overrightarrow{\omega_{b}}\otimes q^{*}$

其中 $\overrightarrow{\omega_{n}}$ 为旋转轴， $\left | \overrightarrow{\omega_{n}} \right |$ 为旋转的角度 $\theta$ ，转换成四元数为

$q^{'}= \begin{bmatrix} \sin(\frac{\theta}{2}) & \overrightarrow{\omega} \cdot \sin(\frac{\theta}{2})\\ \end{bmatrix}$

其中 $\overrightarrow{\omega_{n}}$ 需要归一化，将其应用到初始四元数即可得到当前姿态的四元数
$q^{'} \otimes q$

以下是使用Eigen3的代码示例

#include "Eigen/Core"
#include "Eigen/Geometry"
#include <cmath>

// 陀螺仪测量数据
float gyro[3];

// 初始四元数
Eigen::Quaternionf quaternion = Eigen::Quaternionf(1.0f, 0.0f, 0.0f, 0.0f);

while (1) {
	// 读取陀螺仪数据，单位mdegree/s
	read_data(gyro);

	// 转为向量，单位degree/s
	Eigen::Vector3f gyroscope = Eigen::Vector3f(gyro[0] / 1000.0f, gyro[1] / 1000.0f, gyro[2] / 1000.0f);

	// 时间间隔dt，单位s
    float dt = get_dt() / 1000.0f;
    
    // 角速度向量，单位rad/s
    Eigen::Vector3f omega = gyroscope * M_PI / 180.0f * dt;
    
    // 转换到导航坐标系
    omega = quaternion.toRotationMatrix() * omega;
    
    // 旋转角度
    float theta = omega.norm();
	// 旋转对应的四元数
    omega = omega.normalized() * std::sin(theta / 2.0f);
    Eigen::Quaternionf q = Eigen::Quaternionf(std::cos(theta / 2.0f), omega.x(), omega.y(), omega.z());

	// 应用旋转
    quaternion = (q * quaternion).normalized();
}