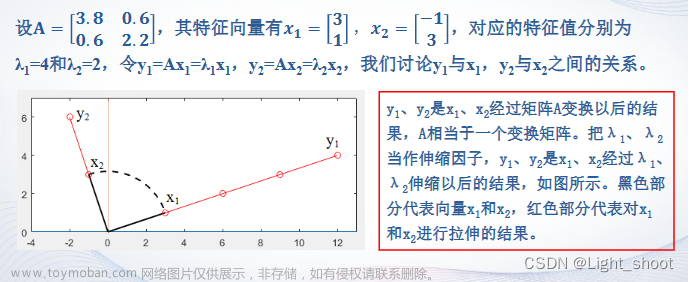
所谓矩阵的分解,就是将一个矩阵写成结构比较简单的或性质比较熟悉的另一些矩阵的乘积。矩阵的分解方法有很多种,包括三角分解、QR(正交三角)分解、最大秩分解、奇异值分解和谱分解,所有这些分解在数值代数和最优化问题的解法中都扮演着十分重要的角色。

本文介绍矩阵的谱分解(Eigen decomposition / Spectral decomposition),不多废话了、直接进入正题、
* * * * * *
设矩阵 有特征根 ,其对应的特征向量为 , 根据定义有
同时,矩阵A和它的转置 的特征值是相同的,都是 ,因为它们的特征多项式是相同的:
因此,存在向量 ,使得
将上式取转置,有
这里,称 为A的左特征向量, 则为A的右特征向量.
由此可知,对于矩阵A的每一个特征值 ,存在向量 和 使
,
A的特征根如果全不同(若相同,此种情况在下文介绍),设为 ,就有2n个向量 ,,i=1,2,...,n,使
, ,
记 ,则有
其中 为对应特征值构成的对角矩阵.
* * * * * *
要使A表示成其他矩阵的乘积(谱分解的形式),需要上式中的U和V可逆(右乘它的逆矩阵),即要证明 和 存在,这等同于证明 是线性无关的,下面给出证明(反证法证明其中一组,另一组同理):
若 是线性相关的,那么存在一组不全为0的数 ,使得
①
于是就有
②
由于 中至少有一个不为0,所以可以
③ 将某个 用其他的向量 来表示,并将其代入②中的 ,这样可以消去一个
不妨记为消去 ,在代入消去后,就有不全为0的 ,使得 ,重复③的做法,逐一消去后得到 ,考虑到矩阵的特征向量不为零向量,所以原假设错误,由此证明U是可逆的,同理,V也是可逆的.
* * * * * *
又因为
于是,当 时, 对一切 成立,也即
易见 存在,且 ,即 ,由 ,就有
时A的特征向量,那么 仍然是A的特征向量,适当选取 以及 ,使得 ,于是 ,因此有
上式就是矩阵的谱分解,特征根 也称为矩阵A的谱.
易见, 就是一个矩阵,因此A被分解为n个矩阵 的线性组合的形式,其系数就是A的谱.
* * * * * *
另外,若A的特征根有重根,例如 是A的 重根,若相应于 有 个线性无关的特征向量,那么上面的讨论仍可以进行. 但是如果A的某个特征根的重数与它的线性无关的特征向量个数不相同,那么谱分解就不成立.文章来源:https://www.toymoban.com/news/detail-451364.html
分享 交流 点赞鼓励 :-) 文章来源地址https://www.toymoban.com/news/detail-451364.html
到了这里,关于矩阵的谱分解 (详细推导步骤~~~特征值分解特征向量的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!