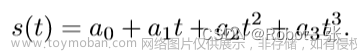自动驾驶规划模块学习笔记-多项式曲线

自动驾驶运动规划中会用到各种曲线，主要用于生成车辆变道的轨迹，高速场景中使用的是五次多项式曲线，城市场景中使用的是分段多项式曲线（piecewise），相比多项式，piecewise能够生成更为复杂的路径。另外对于自由空间，可以使用A*搜索出的轨迹再加以cilqr加以平滑，也能直接供控制使用。下面的内容不一定都对，欢迎大家一起交流学习~

目录

基础类

三次多项式曲线

四次多项式曲线

五次多项式曲线

下期预告：piecewise曲线 

基础类

// 基类Curve1d，定义一维曲线（变量是时间）
class Curve1d {
 public:
  // 构造函数
  Curve1d() = default;
  // 拷贝构造函数
  Curve1d(const Curve1d& other) = default;
  // 有继承的基类的析构函数需要定义为虚函数
  virtual ~Curve1d() = default;
  // 纯虚函数，子类实现，曲线不同阶数对应的param时刻的结果
  virtual double Evaluate(const std::uint32_t order, const double param) const = 0;
  // 纯虚函数，子类实现，时长
  virtual double ParamLength() const = 0;
};

三次多项式曲线

构造函数定义

x0初始位置，dx0初始速度，ddx0初始加速度，x1终点位置，param时间长度，这个很好理解

// 定义了两种构造函数的实现

// 第一种构造函数的实现是直接调用第二种构造函数
CubicPolynomialCurve1d::CubicPolynomialCurve1d(const std::array<double, 3>& start, const double end, const double param)
    : CubicPolynomialCurve1d(start[0], start[1], start[2], end, param) {}

// 第二种构造函数，x0初始位置，dx0初始速度，ddx0初始加速度，x1终点位置，param时间长度
CubicPolynomialCurve1d::CubicPolynomialCurve1d(const double x0, const double dx0, const double ddx0, const double x1,
                                               const double param) {
  ComputeCoefficients(x0, dx0, ddx0, x1, param);
  param_ = param;
  start_condition_[0] = x0;
  start_condition_[1] = dx0;
  start_condition_[2] = ddx0;
  end_condition_ = x1;
}

计算多项式系数

方法1：一般地，自动驾驶里初始状态对应的是当前时刻，规划时长为param的轨迹，可以理解初始状态即为0时刻的状态，这样的话，多项式系数就很好求出来了

void CubicPolynomialCurve1d::ComputeCoefficients(const double x0, const double dx0, const double ddx0, const double x1,
                                                 const double param) {
  assert(param > 0.0);
  const double p2 = param * param;
  const double p3 = param * p2;
  coef_[0] = x0;
  coef_[1] = dx0;
  coef_[2] = 0.5 * ddx0;
  coef_[3] = (x1 - x0 - dx0 * param - coef_[2] * p2) / p3;
}

方法2：已知初始和终点的位置和速度，没有加速度，也比较简单，C2和C3需要手动推算下

, p为终点时刻

// 注意这里的返回类型，用到了this指针，相当于返回一个实例化的类
CubicPolynomialCurve1d& CubicPolynomialCurve1d::FitWithEndPointFirstOrder(const double x0, const double dx0, const double x1, 
                                                                          const double dx1, const double param) {
  if (param <= 0.0) {
    return *this;
  }
  param_ = param;
  coef_[0] = x0;
  coef_[1] = dx0;

  double param2 = param * param;
  double param3 = param2 * param;
  
  double b0 = dx1 + 2 * coef_[1];
  double b1 = dx1 + coef_[1];

  coef_[2] = (3 * x1 - b0 * param -3 * coef_[0]) / param2;
  coef_[3] = (2 * coef_[0] + b1 * param - 2 * x1) / param3;

  return *this;
}

方法3：通过四次多项式曲线来推算，这里用到四次多项式求导为三次多项式的关系

以此类推

// 这里为什么要用静态类型转换static_cast
void CubicPolynomialCurve1d::DerivedFromQuarticCurve(const PolynomialCurve1d& other) {
  assert(other.Order() == 4);
  param_ = other.ParamLength();
  for (size_t i = 1; i < 5; ++i) {
    coef_[i - 1] = other.Coef(i) * static_cast<double>(i);
  }
}

多项式曲线阶数求值

这里代码有点没太看懂，p是param的几次方？

double CubicPolynomialCurve1d::Evaluate(const std::uint32_t order, const double p) const {
  switch (order) {
    case 0: {
      return ((coef_[3] * p + coef_[2]) * p + coef_[1]) * p + coef_[0];
    }
    case 1: {
      return (3.0 * coef_[3] * p + 2.0 * coef_[2]) * p + coef_[1];
    }
    case 2: {
      return 6.0 * coef_[3] * p + 2.0 * coef_[2];
    }
    case 3: {
      return 6.0 * coef_[3];
    }
    default:
      return 0.0;
  }
}

四次多项式曲线

构造函数

 四次多项式有五个系数，所以需要五个状态量

QuarticPolynomialCurve1d::QuarticPolynomialCurve1d(
    const std::array<double, 3>& start, const std::array<double, 2>& end,
    const double param)
    : QuarticPolynomialCurve1d(start[0], start[1], start[2], end[0], end[1],
                               param) {}

QuarticPolynomialCurve1d::QuarticPolynomialCurve1d(
    const double x0, const double dx0, const double ddx0, const double dx1,
    const double ddx1, const double param) {
  param_ = param;
  start_condition_[0] = x0;
  start_condition_[1] = dx0;
  start_condition_[2] = ddx0;
  end_condition_[0] = dx1;
  end_condition_[1] = ddx1;
  ComputeCoefficients(x0, dx0, ddx0, dx1, ddx1, param);
}

求解多项式系数

方法1：已知初始状态x0,dx0,ddx0和终点状态dx1,ddx1，相当于终点的位置是不确定的。代码中C3和C4计算没有使用C1和C2，是避免计算过程中带来的误差，是一种较好的处理方法。但阅读起来可能不直观，可以参考下面公式，实质是一样的。

void QuarticPolynomialCurve1d::ComputeCoefficients(
    const double x0, const double dx0, const double ddx0, const double dx1,
    const double ddx1, const double p) {
  CHECK_GT(p, 0.0);

  coef_[0] = x0;
  coef_[1] = dx0;
  coef_[2] = 0.5 * ddx0;

  double b0 = dx1 - ddx0 * p - dx0;
  double b1 = ddx1 - ddx0;

  double p2 = p * p;
  double p3 = p2 * p;

  coef_[3] = (3 * b0 - b1 * p) / (3 * p2);
  coef_[4] = (-2 * b0 + b1 * p) / (4 * p3);
}

方法2和3：终点或初始位置的加速度不确定，已知其他参数，推导过程与上面类似，注意这里返回的是实例化的类

QuarticPolynomialCurve1d& QuarticPolynomialCurve1d::FitWithEndPointFirstOrder(
    const double x0, const double dx0, const double ddx0, const double x1,
    const double dx1, const double p) {
  CHECK_GT(p, 0.0);

  param_ = p;

  coef_[0] = x0;

  coef_[1] = dx0;

  coef_[2] = 0.5 * ddx0;

  double p2 = p * p;
  double p3 = p2 * p;
  double p4 = p3 * p;

  double b0 = x1 - coef_[0] - coef_[1] * p - coef_[2] * p2;
  double b1 = dx1 - dx0 - ddx0 * p;

  coef_[4] = (b1 * p - 3 * b0) / p4;
  coef_[3] = (4 * b0 - b1 * p) / p3;
  return *this;
}
QuarticPolynomialCurve1d& QuarticPolynomialCurve1d::FitWithEndPointSecondOrder(
    const double x0, const double dx0, const double x1, const double dx1,
    const double ddx1, const double p) {
  CHECK_GT(p, 0.0);

  param_ = p;

  coef_[0] = x0;

  coef_[1] = dx0;

  double p2 = p * p;
  double p3 = p2 * p;
  double p4 = p3 * p;

  double b0 = x1 - coef_[0] - coef_[1] * p;
  double b1 = dx1 - coef_[1];
  double c1 = b1 * p;
  double c2 = ddx1 * p2;

  coef_[2] = (0.5 * c2 - 3 * c1 + 6 * b0) / p2;
  coef_[3] = (-c2 + 5 * c1 - 8 * b0) / p3;
  coef_[4] = (0.5 * c2 - 2 * c1 + 3 * b0) / p4;

  return *this;
}

方法4和5：根据三次多项式积分或五次多项式微分得到

QuarticPolynomialCurve1d& QuarticPolynomialCurve1d::IntegratedFromCubicCurve(
    const PolynomialCurve1d& other, const double init_value) {
  CHECK_EQ(other.Order(), 3U);
  param_ = other.ParamLength();
  coef_[0] = init_value;
  for (size_t i = 0; i < 4; ++i) {
    coef_[i + 1] = other.Coef(i) / (static_cast<double>(i) + 1);
  }
  return *this;
}

QuarticPolynomialCurve1d& QuarticPolynomialCurve1d::DerivedFromQuinticCurve(
    const PolynomialCurve1d& other) {
  CHECK_EQ(other.Order(), 5U);
  param_ = other.ParamLength();
  for (size_t i = 1; i < 6; ++i) {
    coef_[i - 1] = other.Coef(i) * static_cast<double>(i);
  }
  return *this;
}

多项式曲线阶数求值

double QuarticPolynomialCurve1d::Evaluate(const std::uint32_t order,
                                          const double p) const {
  switch (order) {
    case 0: {
      return (((coef_[4] * p + coef_[3]) * p + coef_[2]) * p + coef_[1]) * p +
             coef_[0];
    }
    case 1: {
      return ((4.0 * coef_[4] * p + 3.0 * coef_[3]) * p + 2.0 * coef_[2]) * p +
             coef_[1];
    }
    case 2: {
      return (12.0 * coef_[4] * p + 6.0 * coef_[3]) * p + 2.0 * coef_[2];
    }
    case 3: {
      return 24.0 * coef_[4] * p + 6.0 * coef_[3];
    }
    case 4: {
      return 24.0 * coef_[4];
    }
    default:
      return 0.0;
  }
}

五次多项式曲线

整体思路和四次多项式类型，附上代码，可以参考上面思路理解

在具体代码实现时，数值求解比矩阵计算效率更高文章来源地址https://www.toymoban.com/news/detail-451500.html

QuinticPolynomialCurve1d::QuinticPolynomialCurve1d(
    const std::array<double, 3>& start, const std::array<double, 3>& end,
    const double param)
    : QuinticPolynomialCurve1d(start[0], start[1], start[2], end[0], end[1],
                               end[2], param) {}

QuinticPolynomialCurve1d::QuinticPolynomialCurve1d(
    const double x0, const double dx0, const double ddx0, const double x1,
    const double dx1, const double ddx1, const double param) {
  ComputeCoefficients(x0, dx0, ddx0, x1, dx1, ddx1, param);
  start_condition_[0] = x0;
  start_condition_[1] = dx0;
  start_condition_[2] = ddx0;
  end_condition_[0] = x1;
  end_condition_[1] = dx1;
  end_condition_[2] = ddx1;
  param_ = param;
}
void QuinticPolynomialCurve1d::ComputeCoefficients(
    const double x0, const double dx0, const double ddx0, const double x1,
    const double dx1, const double ddx1, const double p) {
  CHECK_GT(p, 0.0);

  coef_[0] = x0;
  coef_[1] = dx0;
  coef_[2] = ddx0 / 2.0;

  const double p2 = p * p;
  const double p3 = p * p2;

  // the direct analytical method is at least 6 times faster than using matrix
  // inversion.
  const double c0 = (x1 - 0.5 * p2 * ddx0 - dx0 * p - x0) / p3;
  const double c1 = (dx1 - ddx0 * p - dx0) / p2;
  const double c2 = (ddx1 - ddx0) / p;

  coef_[3] = 0.5 * (20.0 * c0 - 8.0 * c1 + c2);
  coef_[4] = (-15.0 * c0 + 7.0 * c1 - c2) / p;
  coef_[5] = (6.0 * c0 - 3.0 * c1 + 0.5 * c2) / p2;
}
void QuinticPolynomialCurve1d::IntegratedFromQuarticCurve(
    const PolynomialCurve1d& other, const double init_value) {
  CHECK_EQ(other.Order(), 4U);
  param_ = other.ParamLength();
  coef_[0] = init_value;
  for (size_t i = 0; i < 5; ++i) {
    coef_[i + 1] = other.Coef(i) / (static_cast<double>(i) + 1);
  }
}
double QuinticPolynomialCurve1d::Evaluate(const uint32_t order,
                                          const double p) const {
  switch (order) {
    case 0: {
      return ((((coef_[5] * p + coef_[4]) * p + coef_[3]) * p + coef_[2]) * p +
              coef_[1]) *
                 p +
             coef_[0];
    }
    case 1: {
      return (((5.0 * coef_[5] * p + 4.0 * coef_[4]) * p + 3.0 * coef_[3]) * p +
              2.0 * coef_[2]) *
                 p +
             coef_[1];
    }
    case 2: {
      return (((20.0 * coef_[5] * p + 12.0 * coef_[4]) * p) + 6.0 * coef_[3]) *
                 p +
             2.0 * coef_[2];
    }
    case 3: {
      return (60.0 * coef_[5] * p + 24.0 * coef_[4]) * p + 6.0 * coef_[3];
    }
    case 4: {
      return 120.0 * coef_[5] * p + 24.0 * coef_[4];
    }
    case 5: {
      return 120.0 * coef_[5];
    }
    default:
      return 0.0;
  }
}

下期预告：piecewise曲线 

到了这里，关于自动驾驶规划模块学习笔记-多项式曲线的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！