一 、目的:
- 掌握指针变量、动态变量的含义;
- 掌握二叉树的结构特征,以及各种存储结构的特点及适用范围;
- 掌握指针类型描述、访问和处理二叉树的运算;
二 、环境:
operating system version:Win11
CPU instruction set: x64
Integrated Development Environment:Viusal Studio 2022
三 、内容:
已知以二叉树表作为存储结构,写出按层次顺序遍历二叉树的算法。
算法思想:本算法采用一个队列q,先将二叉树根结点入队列,然后退队列,输出该结点,若它有左子树,便将左子树根结点入队列;若有右子树,便将右子树根结点入队列,直到队列空为止。因为队列的特点是先进先出,从而达到按层次顺序遍历二叉树的目的。
四 、要求:
- 实现二叉树表的层次遍历算法,并给出应用。
五 、步骤:
1. 程序:
#include "stdio.h"
#include "stdlib.h"
#define INITQUEUE 20
typedef struct BiTNode
{
char data; //定义结点数据
struct BiTNode* lchild;//定义结点左孩子指针
struct BiTNode* rchild;//定义结点右孩子指针
}BiTNode, * BiTree;//定义二叉树结点
typedef struct Queue
{
BiTNode* front;//定义队列头指针
BiTNode* tail;//定义队列尾指针
int size;//定义队列空间大小
}Queue;
int InitQueue(Queue& Q)
{//InitQueue初始化队列
Q.front = (BiTNode*)malloc(INITQUEUE * sizeof(BiTNode));
if (!Q.front)
{
return 0;
}
Q.tail = Q.front;
Q.size = INITQUEUE;
return 1;
}
bool IsEmpty(Queue Q)
{//IsEmpty判断队列是否为空
if (Q.tail == Q.front)
{
return true;
}
else
{
return false;
}
}
int EnQueue(Queue& Q, BiTNode e)
{//EnQueue将元素入队列
if ((Q.tail - Q.front + INITQUEUE) % INITQUEUE == INITQUEUE - 1)
{
return 0;
}
*Q.tail = e;
Q.tail++;
return 1;
}
int DeQueue(Queue& Q, BiTNode& e)
{//DeQueue将元素出队列
if (Q.front == Q.tail)
{
return 0;
}
e = *Q.front;
Q.front++;
return 1;
}
void CreateBiTree(BiTree& T)
{//构造二叉树
char ch;
scanf_s("%c", &ch);
if ('#' == ch)
{
T = NULL;
}
else
{
T = (BiTree)malloc(sizeof(BiTNode));
T->data = ch;
CreateBiTree(T->lchild);
CreateBiTree(T->rchild);
}
}
int levelTraverse(BiTree T)
{//二叉树层次遍历
if (NULL == T)
{
return 0;
}
BiTNode e;
Queue Q;
int levelcount = 0; //树的深度
int curlevel = 1; //本层里剩余的未访问的结点数
int nextlevel = 0; //下一层还未访问的结点数
InitQueue(Q);
EnQueue(Q, *T);
while (!IsEmpty(Q))//当队列不为空时循环
{
DeQueue(Q, e);//出队列
printf("%c ", e.data);//打印该元素
curlevel--;
if (NULL != e.lchild)//若左子树不为空
{
EnQueue(Q, *e.lchild);//将元素入队列
nextlevel++;//下一层数自增
}
if (NULL != e.rchild)//若右子树不为空
{
EnQueue(Q, *e.rchild);//将元素入队列
nextlevel++;
}
if (0 == curlevel)
{
levelcount++;
printf("——Layer %d node traversal.\n", levelcount);
curlevel = nextlevel;
nextlevel = 0;
}
}
return 1;
}
int main(int argc, char* argv[])
{
BiTree T = NULL;
printf_s("Please enter the binary tree node:\n");
CreateBiTree(T);
printf_s("Binary tree created successfully.\n");
printf_s("The hierarchical order traversal of this binary tree is:\n");
levelTraverse(T);
return 0;
}
2.程序结果:
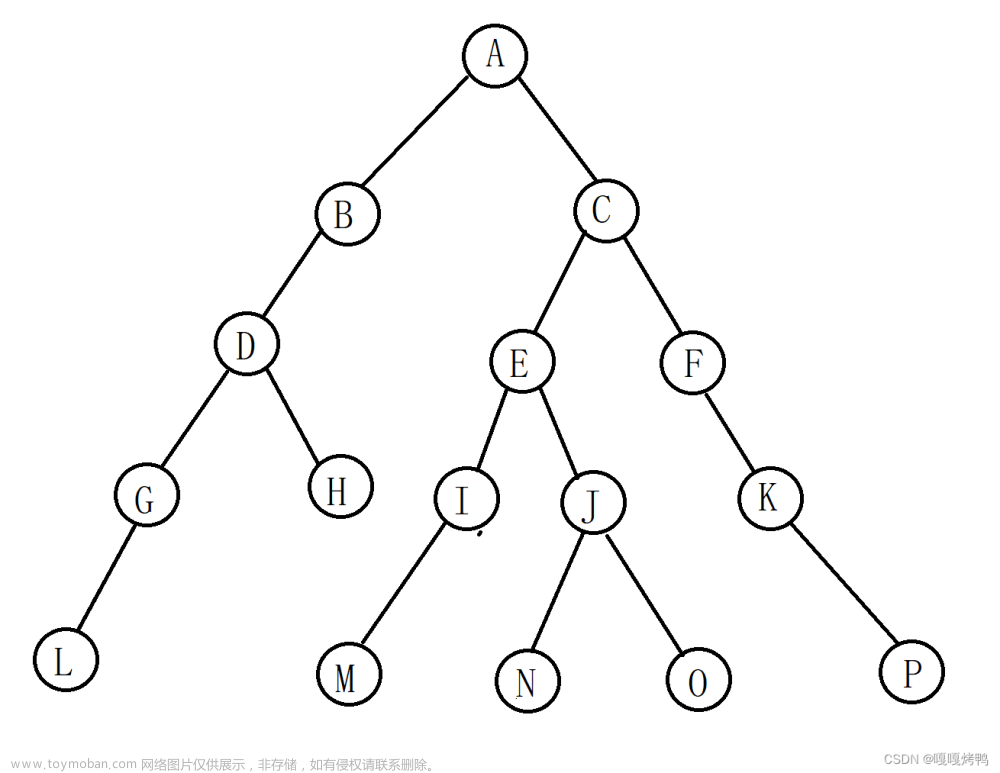
程序运行,在此次、中我使用了二叉树如下

作为测试样例,因此输入ABC##D##EF##G##。其中定义符号“#”为空结点。、结果如下图所示:

由输出结果可知,按照层次遍历的顺序分别输出了每一层的元素,可知算法正确实现了二叉树的层次遍历。
3.分析和改进应用:
分析:此次、的整体思路是:层次遍历借助队列实现,首先先定义二叉树及队列的初始3.化,按照常规的方式分别定义队列的判断空IsEmpty函数,入队函数EnQueue与出队函数DeQueue,在二叉树的层次遍历levelTraverse方法中,将二叉树的根结点进入队列中,判断队列不为NULL。打印输出该结点存储的元素。判断结点如果有孩子(左孩子、右孩子),就将孩子进入队列中。循环以上操作,直到 BT->lchild == NULL、BT->rchild=NULL。
改进应用:基于二叉树的层次的层次遍历,可以改进一个有关于二叉树层次遍历的应用,即利用层次遍历求出二叉树的宽度。二叉树的宽度是指二叉树各层结点个数的最大值。因为二叉树的层次遍历借助于队列实现,每次打印当前结点后将其左子树右子树入队,此时队列中既包含当前层的结点,也包含下一层的结点,若我们将当前层的结点全部出队,剩余的就是下一层的结点个数。所以,可以使用maxWidth来表示最大宽度,若下一层的结点个数大于maxWidth,则更新maxWidth,最终队列为空,得到的maxWidth即为二叉树的宽度。实现的函数代码如下:
int WidthCount ( BiTree root) {
Queue Q;
BiTree T;
if (!root)
return; //若是空树则直接返回
InitQueue(Q); // 初始化空队列Q
int width = 0;
int num = 1;
int maxWidth = 0;
EnQueue(Q,root);
while (!IsEmpty(Q))
{
DeQueue(Q,T);
printf("%d ", T->Data); // 访问取出队列的结点
if ( T->lchild )
EnQueue(Q, T->lchild); width++;
if ( T->rchild )
EnQueue(Q, T->rchild); width++;
if(--num == 0){
num = witdh;
if(maxWidth < width){
maxWidth = width;
}
width = 0;
}
}
return maxWidth ;
}
六 、小结:文章来源:https://www.toymoban.com/news/detail-451758.html
此次是有关于二叉树层次遍历算法的实现,算法的思想比较清晰,即先定义一个循环队列,使这个队中的数据域存放二叉树中的元素。先将二叉树根结点入队,然后出队,访问该结点,如果有左子树,则将左子树根结点入队;如果存在右子树,则将右子树的根结点入队。然后出队,对出队结点访问,如此循环直到队列为空。最终,出队的顺序就是层次遍历的顺序。关于层次遍历的应用,我是在层次遍历中的特殊结构,即打印结点后把它左右子树入队,该队列中有当前层的结点,也有下一层结点,因此可以将当前层的结点全部出队,剩下的为下一层的结点个数,然后只需要比较当前最多的层结点和下一层结点数的大小即可。文章来源地址https://www.toymoban.com/news/detail-451758.html
到了这里,关于二叉树的编程与实现(C语言)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!