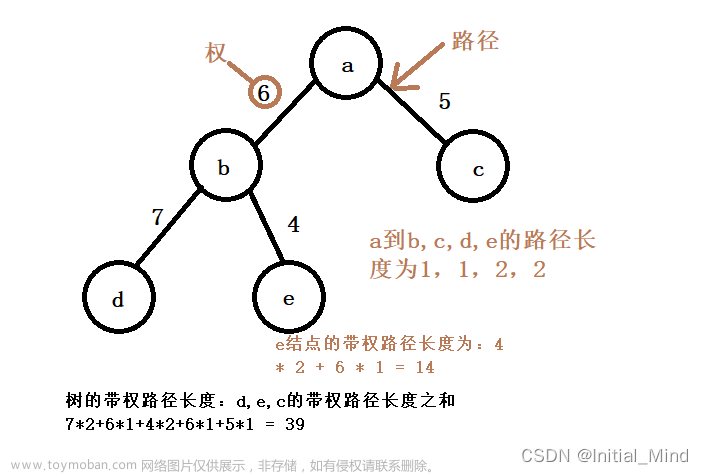
哈夫曼树的构造过程:
(1) 以权值分别为W1,W2...Wn的n各结点,构成n棵二叉树T1,T2,...Tn并组成森林F={T1,T2,...Tn},其中每棵二叉树 Ti仅有一个权值为 Wi的根结点;
(2) 在F中选取两棵根结点权值最小的树作为左右子树构造一棵新二叉树,并且置新二叉树根结点权值为左右子树上根结点的权值之和(根结点的权值=左右孩子权值之和,叶结点的权值= Wi)
(3) 从F中删除这两棵二叉树,同时将新二叉树加入到F中;
(4) 重复(2)、(3)直到F中只含一棵二叉树为止,这棵二叉树就是Huffman树。
参考《数据结构(C语言版)(第二版)》(严蔚敏编)第138页)
哈夫曼树存储结构:
一棵有n个叶子结点的哈夫曼树共有2n-1个结点,可以将其存于一个大小为2n-1的数组中,为了方便(第i个结点用下标为i表示),所以将数组0号单元置空,故数组的大小为2n。哈夫曼树对于一个结点来说需要存储其权值、双亲及左右孩子,因此哈夫曼树的存储表示如下:
typedef struct {
//定义一个结构体数组
int weight;//权重
int p, lc, rc;//结点双亲及左右孩子下标
}*HuffmanTree,HTNode;将叶子结点集中存储在1~n的位置,后面的n-1个位置存储非叶子结点。
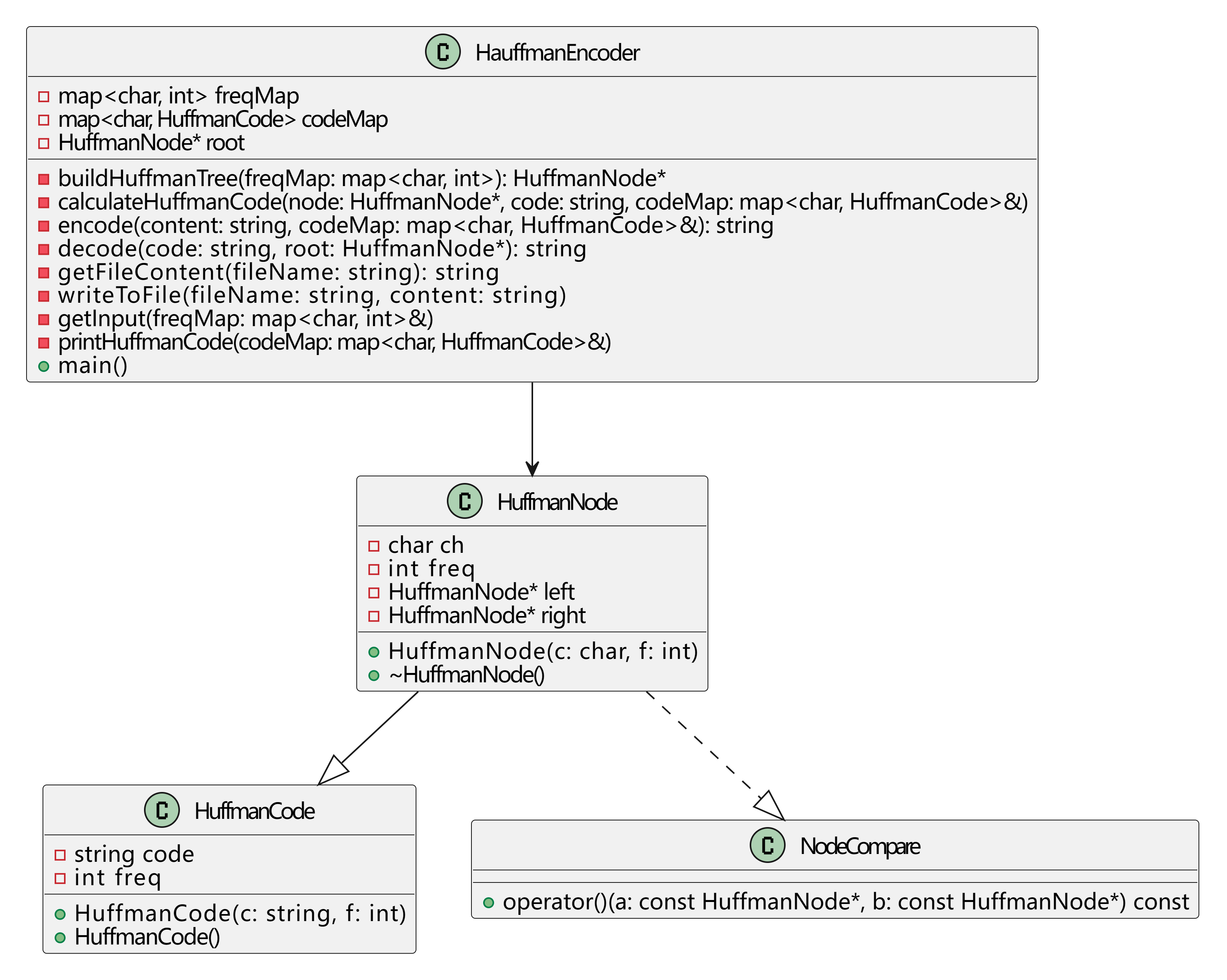
哈夫曼树构造的算法实现:
构造huffmantree大致分为两大步骤:
1.初始化
2.创建树
严蔚敏版的《数据结构(c语言版)(第二版)》对其算法描述如下:
void CreateHuffmanTree(HuffmanTree &T, int n){
//初始化
if(n <= 1) return;
m = 2*n-1;
T = new HTNode[m+1];//0号单元未用,动态分配m+1个单元
for(1 = 1;i <= m;i++){
T[i].p = 0;
T[i].lc = 0;
T[i].rc = 0;
}
for(i = 1;i <= n;i++){
cin>>T[i].weight //依次输入前n个叶子结点的权值
}
/*----------------初始化结束,下面开始创建哈夫曼树--------------------*/
for(i = n+1;i <= m;i++){
//n个叶子结点,2n-1个结点,共要n-1次合并产生n-1个新的结点
Select(T,i-1,s1,s2);
//在T[k]中 (k范围为[1,i-1])找到两个权值最小且双亲域为0的结点,返回它们在T中的序号s1,s2
T[s1].p = i; T[s2].p = i; //得到新结点i,从森林中删除s1、s2,将s1、s2的双亲域改为i
T[i].lc = s1; T[i].rc = s2; //s1、s2分别作为i的左右孩子
T[i].weight = T[s1].weight + T[s2].weight; //i的权值为左右孩子之和
}
}具体实现的时候,除了一些初始化和语法规范,主要的是写出select函数,由于刚刚开始学,自身代码水平不行笔者在写select函数的时候遇到了不少麻烦。
要找权值最小的两个下标可以如下实现:
int min1 = 100;
int min2 = 100;
//定义min1,min2分别为最小值和次小值,赋一个很大的值(至少比叶子结点最大的权重要大)这里以100为例子
for (int j = 1;j <= i - 1;j++) {
if (T[j].p == 0) {
//条件为双亲域为0
if (T[j].weight < min1) {
min2 = min1;
min1 = T[j].weight;
//如果第j个结点的权重比最小值小,min2更新为min1,min1更新为第j个结点的权重
}
else if (T[j].weight <= min2) {
min2 = T[j].weight;
//如果第j个结点的权重比次小值min2还小,那min2更新为该值
}
}
}
//上述循环中找到两个最小值,但要求的是两个下标,故再次循环找
for (int j = 1;j <= i - 1;j++) {
if (T[j].p == 0 && T[j].weight == min1) {
s1 = j;
//这里要注意不要忘记双亲域为0的条件,如果已经合并过的结点(双亲域不为0)的权值恰好等于这一次合并的最小值,就会出错
}
}
for (int j = 1;j <= i - 1;j++){
if (T[j].p == 0 && T[j].weight == min2 && j != s1) {
s2 = j;
//这里还得添加一个条件,也就是s1!=s2
//如果min1 = min2,但此时j1!=j2,也就是下标不同,如果不加该条件的话s1和s2的值相同,也就是只找到了一个值,也会报错
}如果像算法描述的那样,s1、s2作为select的参数很难定义和初始化,因此不如将:
T[s1].p = i;
T[s2].p = i;
T[i].lc = s1;
T[i].rc = s2;
T[i].weight = T[s1].weight + T[s2].weight;
这一段放到select函数里实现,再将i作为参数传到select函数中就会方便许多。
完整代码实现:
测试的以书上的例题w = {5,29,7,8,14,23,3,11} 为例,n = 8,m = 15
测试第14、15个结点的权值、双亲及左右孩子的结点(因为一开始逐步调试的时候这两个结点的错误最多)
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<Windows.h>
#include<malloc.h>
typedef struct {
//定义一个结构体数组
int weight;//权重
int p, lc, rc;//结点双亲及左右孩子下标
}*HuffmanTree,HTNode;
void select(HuffmanTree& T, int n, int i) {
//找T中下标范围1----i-1且双亲域为0的权重最小的两个结点下标为s1,s2
int min1 = 100;
int min2 = 100;
int s1 = 0;
int s2 = 0;
for (int j = 1;j <= i - 1;j++) {
if (T[j].p == 0) {
if (T[j].weight < min1) {
min2 = min1;
min1 = T[j].weight;
}
else if (T[j].weight <= min2) {
min2 = T[j].weight;
}
}
}
for (int j = 1;j <= i - 1;j++) {
if (T[j].p == 0 && T[j].weight == min1) {
s1 = j;
}
}
for (int j = 1;j <= i - 1;j++){
if (T[j].p == 0 && T[j].weight == min2 && j != s1) {
s2 = j;
}
}
T[s1].p = i;
T[s2].p = i;
T[i].lc = s1;
T[i].rc = s2;
T[i].weight = T[s1].weight + T[s2].weight;
}
void CreateHuffmanTree(HuffmanTree& T, int n) {
if (n <= 1) {
return;
}
int m = 2 * n - 1;
//1.初始化数组
T = new HTNode[m + 1];
for (int i = 1;i <= m;i++) {
T[i].p = 0;
T[i].lc = 0;
T[i].rc = 0;
}
for (int i = 1;i <= n;i++) {
printf("第%d个结点权重为:\n", i);
scanf("%d", &(T[i].weight));
}
//2.创建哈夫曼树
for (int i = n + 1;i <= m;i++) {
//n-1次合并,n-1次循环
select(T, n, i);
//找T中下标范围1----i-1且双亲域为0的权重最小的两个结点
}
}
int main() {
HuffmanTree T;
//测试用w = {5,29,7,8,14,23,3,11}
CreateHuffmanTree(T, 8);
printf("%第十四个结点的权重为%d,双亲为%d结点,左孩子为%d结点,右孩子为%d结点\n", T[14].weight,T[14].p,T[14].lc,T[14].rc);//测试用数据
printf("第十五个结点的权重为%d,双亲为%d结点,左孩子为%d结点,右孩子为%d结点\n", T[15].weight,T[15].p,T[15].lc,T[15].rc);
system("pause");
}测试结果如下:
 文章来源:https://www.toymoban.com/news/detail-451834.html
文章来源:https://www.toymoban.com/news/detail-451834.html
ps:笔者第一次写博客,若有代码错误和表述不清还请见谅,谢谢!!!!!!!!!!文章来源地址https://www.toymoban.com/news/detail-451834.html
到了这里,关于哈夫曼树的构造及C++代码实现的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!