题目要求
背景知识
深度优先搜索与 DFS 序
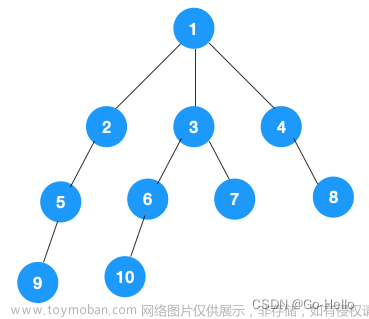
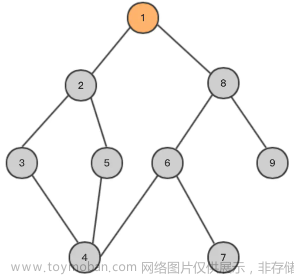
深度优先搜索算法(DFS)是一种用于遍历或搜索树或图的算法。以下伪代码描述了在树 T 上进行深度优先搜索的过程:
procedure DFS(T, u, L) // T 是被深度优先搜索的树
// u 是当前搜索的节点
// L 是一个链表,保存了所有节点被第一次访问的顺序
append u to L // 将节点 u 添加到链表 L 的末尾
for v in u.children do // 枚举节点 u 的所有子节点 v
DFS(T, v) // 递归搜索节点 v
令 r 为树 T 的根,调用 DFS(T, r, L) 即可完成对 T 的深度优先搜索,保存在链表 L 中的排列被称为 DFS 序。相信聪明的你已经发现了,如果枚举子节点的顺序不同,最终得到的 DFS 序也会不同。
逆序对
给定一个长度为 n 的整数序列 a1,a2,⋯,an,该序列的逆序对数量是同时满足以下条件的有序数对 (i,j) 的数量:
1≤i<j≤n;
ai>aj。
问题求解
给定一棵 n 个节点的树,其中节点 r 为根。求该树所有可能的 DFS 序中逆序对数量之和。输入格式
第一行输入两个整数 n,r(2≤n≤3×105,1≤r≤n)表示树的大小与根节点。
对于接下来的 (n−1) 行,第 i 行输入两个整数 ui 与 vi(1≤ui,vi≤n),表示树上有一条边连接节点 ui 与 vi。
输出格式
输出一行一个整数,表示该树所有可能的 DFS 序中逆序对数量之和。由于答案可能很大,请对 109+7 取模后输出。
样例输入 1
5 3
1 5
2 5
3 5
4 3
样例输出 1
24
样例输入 2
10 5
10 2
2 5
10 7
7 1
7 9
4 2
3 10
10 8
3 6
样例输出 2
516
解题思路
- 对于给定的树,首先进行DFS遍历,求出每个节点的子树大小 szsz,并将整棵树存储在邻接表中。
- 在DFS遍历过程中,需要维护一个树状数组,表示当前节点的DFS序(或者说时间戳)出现的次数。
每访问到一个新节点 uu 时,通过查询树状数组,统计出其祖先节点的DFS序总和 s1s1,以及 DFS 序比 uu 大的节点的数量 s2s2
具体来说:我们可以用树状数组记录整棵树每个节点出现的次数,然后查询区间 [u+1,n][u+1,n] 的总和,即为 DFS 序比 uu 大的所有节点的出现次数之和。注意需要先将 uu 对应的计数减去 11,因为 uu 自身对统计并不存在。
- 可以通过简单的组合数计算,求出在根节点为 rootroot 的情况下,所有不合法的边的数量。对于每个子树 TT,其内部的边不会对答案贡献,因此只需考虑连接 TT 向其他子树的边。由于连接两个不同子树 T1T1 和 T2T2 的边肯定会造成环的出现,因此我们只需统计在每个 TT 内部,连接其与其它子树的边数即可,
具体数量为 s2⋅(n−sz[u])s2⋅(n−sz[u])
代码
#include<iostream>
#include<vector>
using namespace std;
typedef long long LL;
const int N = 300010, P = 1e9+7;
vector<int> g[N]; // 邻接表存储整张树
int sz[N],tr[N]; // sz数组记录子树大小,tr数组即为树状数组
int n,root;
int sum=1,s1,s2; // sum为阶乘,s1和s2用于统计不合法路径的数量
void add(int x,int y)
{
for(int i=x;i<N;i+=(i&-i))
tr[i]+=y;
}
int query(int x)
{
int res=0;
for(int i=x;i;i-=(i&-i))
res+=tr[i];
return res;
}
void dfs(int u,int fa)
{
add(u,1); // 将节点u对应位置的计数加1(表示u出现了一次)
s1=(s1+query(n)-query(u))%P; // 统计所有深度比u小的节点的DFS序总和
sz[u]=1; // 初始化子树大小为1
int cnt=0; // cnt记录u的子节点个数
for(auto &j:g[u])
{
if(j==fa) continue;
dfs(j,u); // 递归搜索j的子树
sz[u]+=sz[j]; // 更新sz数组
cnt++;
}
for(int i=1;i<=cnt;i++)
sum=(LL)sum*i%P; // 更新阶乘,即(n-sz[u])! 的值
s2=(s2+n-query(n)-sz[u]+1)%P; // 统计DFS序比u大的节点个数
add(u,-1); // 回溯时将u的计数减1(表示u已经不再访问)
}
int main()
{
scanf("%d%d",&n,&root);
for(int i=0;i<n-1;i++)
{
int a,b;
scanf("%d%d",&a,&b);
g[a].push_back(b);
g[b].push_back(a); // 无向图,需要双向添加边
}
dfs(root,-1);
int ans=((LL)s1*sum+(LL)s2*sum%P*(P+1)/4)%P; // 计算ans,具体见下面
printf("%d\n",ans);
return 0;
}
代码解读
首先定义一个数组g[N]来存储整张树的邻接表,并且定义了两个数组sz[N]和tr[N],分别用来记录每个节点的子树大小和树状数组。同时定义了一个常量P,表示取模的数。
vector<int> g[N]; // 邻接表存储整张树
int sz[N],tr[N]; // sz数组记录子树大小,tr数组即为树状数组
const int N = 300010, P = 1e9+7;
对于dfs函数的每个节点u,进行以下处理:
- 将节点u的计数加1,即表示节点u出现了一次。
- 统计所有深度比u小的节点的DFS序总和,通过查询树状数组实现。
- 初始化节点u的子树大小为1,并且统计其子节点的个数。
- 对于每个非父亲节点j,
递归地搜索其子树,并更新sz[u]数组 - 更新阶乘值,具体来说,对于任意一个子节点j,其与其它子节点之间的连接边顺序并不影响路径是否合法,因此我们需要将所有子节点与其它子节点的联系进行组合,而每种组合都只算一次,所以用阶乘来计算。
例如,n−sz[u]n−sz[u]个节点之间的连接关系可以有(n−sz[u])!(n−sz[u])!种组合方式。 - 统计DFS序比u大的节点个数,这可以通过查询区间[u+1,n]的总和实现。注意,查询前需要先将节点u的计数减去1,因为节点u自身对统计无影响。
- 回溯时,需要将节点u的计数减去1,表示节点u已经不再访问。
void dfs(int u,int fa)
{
add(u,1); // 将节点u对应位置的计数加1(表示u出现了一次)
s1=(s1+query(n)-query(u))%P; // 统计所有深度比u小的节点的DFS序总和
sz[u]=1; // 初始化子树大小为1
int cnt=0; // cnt记录u的子节点个数
for(auto &j:g[u])
{
if(j==fa) continue;
dfs(j,u); // 递归搜索j的子树
sz[u]+=sz[j]; // 更新sz数组
cnt++;
}
for(int i=1;i<=cnt;i++)
sum=(LL)sum*i%P; // 更新阶乘,即(n-sz[u])! 的值
s2=(s2+n-query(n)-sz[u]+1)%P; // 统计DFS序比u大的节点个数
add(u,-1); // 回溯时将u的计数减1(表示u已经不再访问)
}
最后,计算不合法路径的数量:对于每个子树TT,其内部的边不会对答案有贡献,因此只需考虑连接 TT 向其他子树的边。由于连接两个不同子树T1T1和T2T2的边肯定会造成环的出现,因此只需统计在每个TT内部,连接其与其它子树的边数即可,具体数量为s2⋅(n−sz[u])s2⋅(n−sz[u])
将s1⋅sums1⋅sum和s2⋅sum⋅(P+1)/4s2⋅sum⋅(P+1)/4相加,即可得到答案。文章来源:https://www.toymoban.com/news/detail-451877.html
int ans=((LL)s1*sum+(LL)s2*sum%P*(P+1)/4)%P;
printf("%d\n",ans);
总结
本文使用树状数组及DFS遍历实现对该题的求解,读者可躬身实践。
我是秋说,我们下次见。文章来源地址https://www.toymoban.com/news/detail-451877.html
到了这里,关于C++/PTA 关于深度优先搜索和逆序对的题应该不会很难吧这件事的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!