正态分布
正态分布,最早由棣莫弗在二项分布的渐近公式中得到,而真正奠定其地位的,应是高斯对测量误差的研究,故而又称Gauss分布。测量是人类定量认识自然界的基础,测量误差的普遍性,使得正态分布拥有广泛的应用场景,或许正因如此,正太分布在分布族谱图中居于核心的位置。
正态分布 N ( μ , σ ) N(\mu, \sigma) N(μ,σ)受到期望 μ \mu μ和方差 σ 2 \sigma^2 σ2的调控,其概率密度函数为
1 2 π σ 2 exp [ − ( x − μ ) 2 2 σ 2 ] \frac{1}{\sqrt{2\pi\sigma^2}}\exp[-\frac{(x-\mu)^2}{2\sigma^2}] 2πσ21exp[−2σ2(x−μ)2]
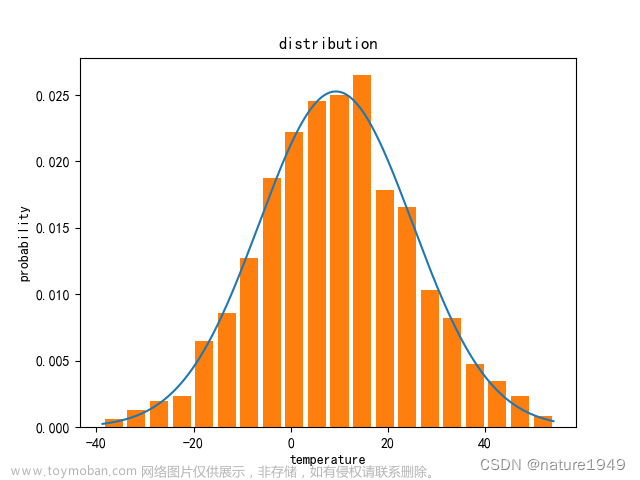
当 μ = 0 \mu=0 μ=0而 σ = 1 \sigma=1 σ=1时,为标准正态分布 N ( 0 , 1 ) N(0,1) N(0,1),对应概率分布函数为 Φ ( x ) = 1 2 π exp [ − x 2 2 ] \Phi(x)=\frac{1}{\sqrt{2\pi}}\exp[-\frac{x^2}{2}] Φ(x)=2π1exp[−2x2],形状如下,

在scipy.stats中,分别封装了正态分布类norm和标准正态分布类halfnorm。
二项分布
二项分布是非常简单而又基础的一种离散分布,貌似是高中学到的第一个分布,就算不是第一个,也是第一批。在 N N N次独立重复的伯努利试验中,设A在每次实验中发生的概率均为 p p p。则 N N N次试验后A发生 k k k次的概率分布,就是二项分布,记作 X ∼ B ( n , p ) X\sim B(n,p) X∼B(n,p),则
P { X = k } = ( n k ) p k ( 1 − p ) n − k P\{X=k\}=\binom{n}{k}p^k(1-p)^{n-k} P{X=k}=(kn)pk(1−p)n−k
其中 ( n k ) = n ! k ! ( n − k ) ! \binom{n}{k}=\frac{n!}{k!(n-k)!} (kn)=k!(n−k)!n!,高中的写法一般是 C n k C^k_n Cnk。
记 q = 1 − p q=1-p q=1−p,令 x k = k − n p n p q x_k=\frac{k-np}{\sqrt{npq}} xk=npqk−np,当 n n n趋近于无穷大时,根据De Moivre–Laplace定理,有
lim n → ∞ n ! k ! ( n − k ) ! p k q n − k ≈ 1 2 π n p q e ( k − n p ) 2 2 n p q \lim_{n\to\infty}\frac{n!}{k!(n-k)!}p^kq^{n-k}\approx\frac{1}{\sqrt{2\pi npq}}e^{\frac{(k-np)^2}{2npq}} n→∞limk!(n−k)!n!pkqn−k≈2πnpq1e2npq(k−np)2
即服从 σ 2 = n p q , μ = n p \sigma^2=npq, \mu=np σ2=npq,μ=np的高斯分布。
验证
下面通过scipy.stats对二项分布和高斯分布之间的关联进行验证
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as ss
p,q = 0.2, 0.8
ns = [10, 100, 1000, 10000]
fig = plt.figure()
for i,n in enumerate(ns):
rs = ss.binom(n, p).rvs(50000)
rv = ss.norm(n*p, np.sqrt(n*p*q))
st, ed = rv.interval(0.999)
xs = np.linspace(st, ed, 100)
ys = rv.pdf(xs)
ax = fig.add_subplot(2,2,i+1)
ax.hist(rs, density=True, bins='auto', alpha=0.2)
ax.plot(xs, ys)
plt.title(f"n={n}")
plt.show()
效果如下,可见随着 n n n越来越大,二项分布的随机数越来越靠近正态分布的概率密度曲线文章来源:https://www.toymoban.com/news/detail-451903.html
 文章来源地址https://www.toymoban.com/news/detail-451903.html
文章来源地址https://www.toymoban.com/news/detail-451903.html
到了这里,关于【分布族谱】正态分布和二项分布的关系的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!