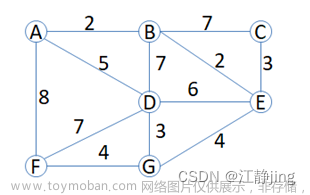
1.最小生成树
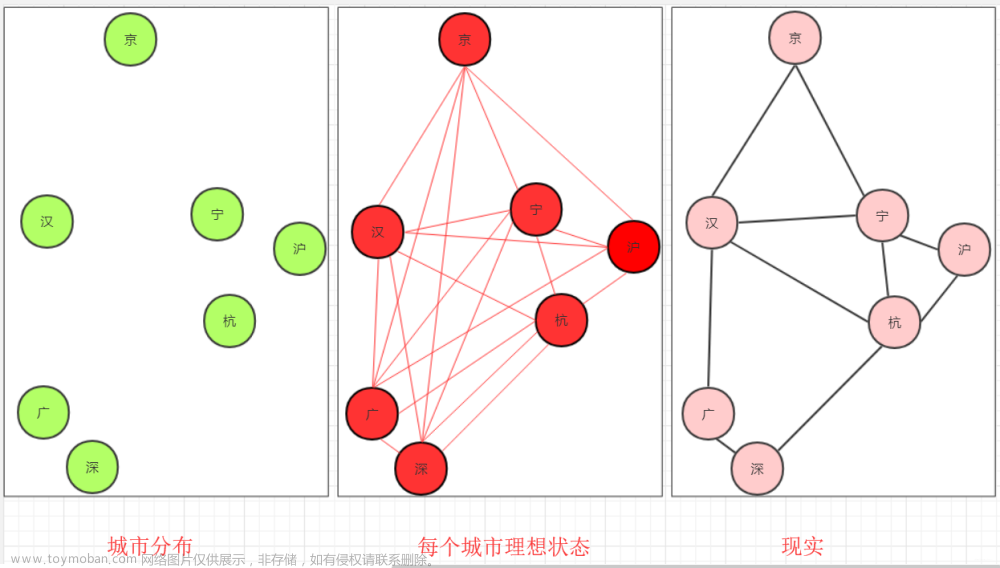
连通图:在无向图中,若从顶点v1到顶点v2有路径,则称顶点v1与顶点v2是连通的。如果图中任
意一对顶点都是连通的,则称此图为连通图。
生成树:一个连通图的最小连通子图称作该图的生成树。有n个顶点的连通图的生成树有n个顶点
和n-1条边。
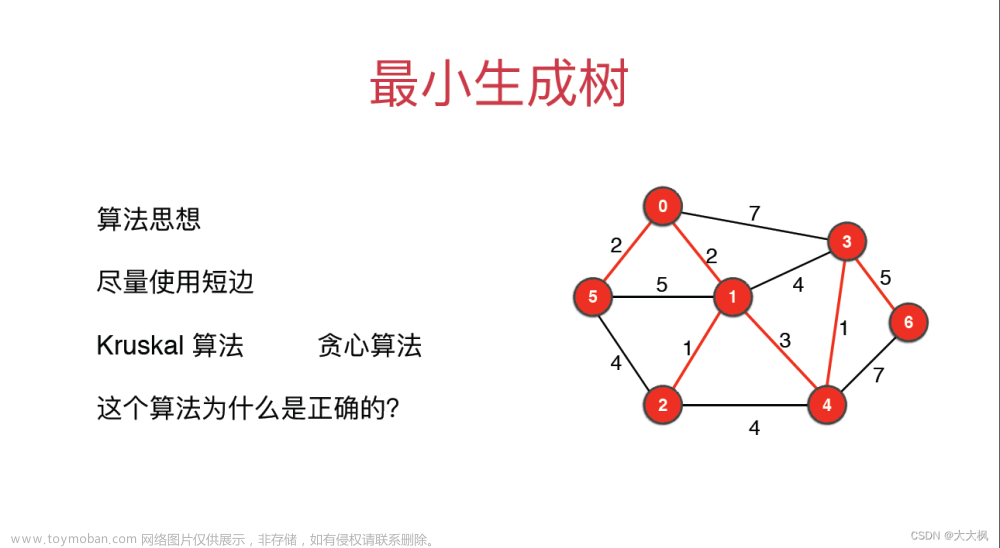
最小生成树:构成生成树的这些边加起来权值最小的
连通图中的每一棵生成树,都是原图的一个极大无环子图,即:从其中删去任何一条边,生成树
就不在连通;反之,在其中引入任何一条新边,都会形成一条回路。
若连通图由n个顶点组成,则其生成树必含n个顶点和n-1条边。因此构造最小生成树的准则有三
条:
1. 只能使用图中权值最小的边来构造最小生成树
2. 只能使用恰好n-1条边来连接图中的n个顶点
3. 选用的n-1条边不能构成回路
构造最小生成树的方法:Kruskal算法和Prim算法。这两个算法都采用了逐步求解的贪心策略。
贪心算法:是指在问题求解时,总是做出当前看起来最好的选择。也就是说贪心算法做出的不是
整体
最优的的选择,而是某种意义上的局部最优解。贪心算法不是对所有的问题都能得到整体最优解。
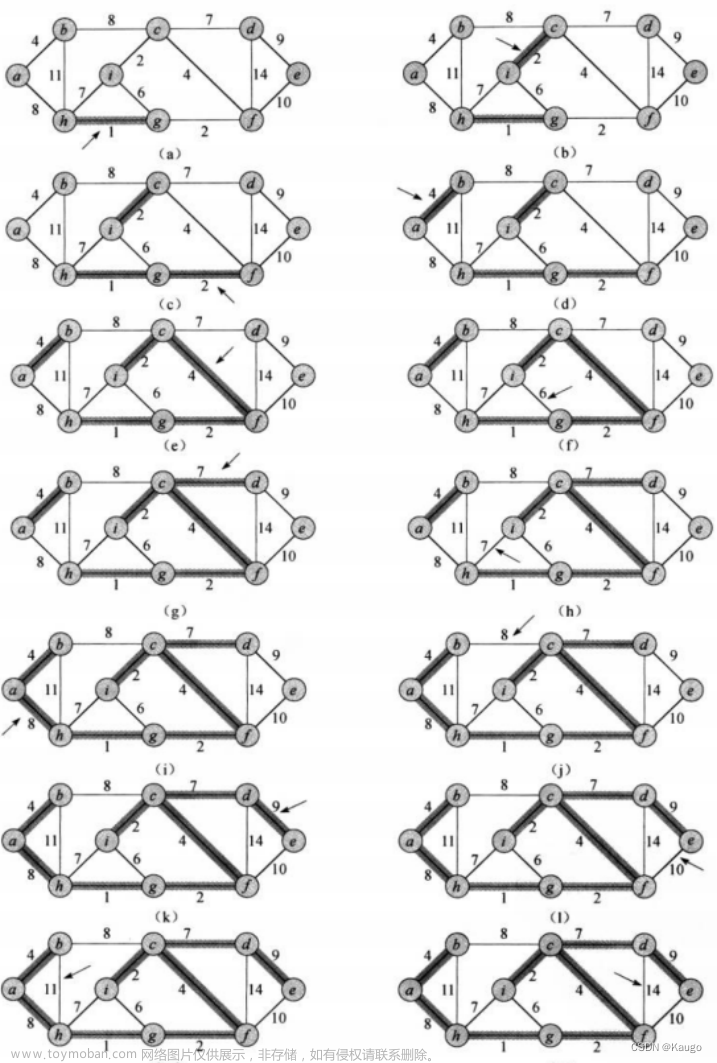
2.Kruskal算法
任给一个有n个顶点的连通网络N={V,E},首先构造一个由这n个顶点组成、不含任何边的图G={V,NULL},其中每个顶点自成一个连通分量,其次不断从E中取出权值最小的一条边(若有多条任取其一),若该边的两个顶点来自不同的连通分量,则将此边加入到G中。如此重复,直到所有顶点在同一个连通分量上为止。
核心:每次迭代时,选出一条具有最小权值,且两端点不在同一连通分量上的边,加入生成树。

实现思路:借助优先级队列将每一条权值按照从小到大的顺序存储起来,依次取出优先级队列中的值,判断当前边做为最小生成树的边是否构成回路,如果构成构成回路则采用并查集进行排除。
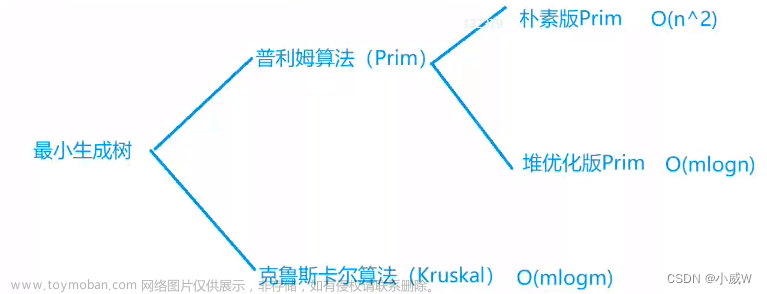
3.Prim算法
 文章来源:https://www.toymoban.com/news/detail-452305.html
文章来源:https://www.toymoban.com/news/detail-452305.html
实现思路:给一个源点,借助两个vector数组X和Y,从X中加入源点,然后在Y中选择权值最小的边添加到优先级队列中,然后依次去除优先级队列中的值,如果最小边的目标点也在X集合中,就说明构成环了,否则该边就是最小边,进行添加边,然后更新X数组和Y数组继续选边文章来源地址https://www.toymoban.com/news/detail-452305.html
4.代码实现
#include<iostream>
#include<vector>
#include<map>
#include<string>
#include<queue>
#include<functional>
using namespace std;
namespace matrix
{
class UnionFindSet
{
public:
UnionFindSet(size_t size)
: _ufs(size, -1) {}
int FindRoot(size_t index)
{
while (_ufs[index] >= 0)
{
index = _ufs[index];
}
return index;
}
bool Union(int x1, int x2)
{
int root1 = FindRoot(x1);
int root2 = FindRoot(x2);
if (root1 == root2)
return false;
_ufs[root1] += _ufs[root2];
_ufs[root2] = root1;
return true;
}
bool InSet(int x1, int x2)
{
return FindRoot(x1) == FindRoot(x2);
}
int Count()
{
int count = 0;
for (auto& e : _ufs)
{
if (e < 0)
count++;
}
return count;
}
private:
vector<int> _ufs;
};
template<class V, class W, W MAX_W = INT_MAX, bool Direction = false>
class Graph
{
typedef Graph<V,W, MAX_W, Direction> self;
public:
Graph() = default;
Graph(const V* vertexs, size_t n)
{
_vertexs.reserve(n);
for (size_t i = 0; i < n; i++)
{
_vertexs.push_back(vertexs[i]);
_indexMap[vertexs[i]] = i;
}
_matrix.resize(n);
for (auto& e : _matrix)
{
e.resize(n, MAX_W);
}
}
void _addEdge(size_t srci, size_t dsti, const W& w)
{
_matrix[srci][dsti] = w;
if (Direction == false)
_matrix[dsti][srci] = w;
}
size_t GetVertexIndex(const V& v)
{
auto ret = _indexMap.find(v);
if (ret != _indexMap.end())
return ret->second;
else
return -1;
}
//添加边:
void AddEdge(const V& src, const V& dst, const W& w)
{
size_t srci = GetVertexIndex(src);
size_t dsti = GetVertexIndex(dst);
_addEdge(srci, dsti, w);
}
void Print()
{
//打印顶点和下标的映射关系
for (size_t i = 0; i < _vertexs.size(); i++)
{
cout << _vertexs[i] << "-" << i << " ";
}
cout << endl;
for (size_t i = 0; i < _vertexs.size(); i++)
{
if (i == 0)
cout << " ";
cout << i << " ";
}
cout << endl;
//打印矩阵:
for (size_t i = 0; i < _matrix.size(); i++)
{
cout << i << " ";
for (size_t j = 0; j < _matrix[i].size(); j++)
{
if (_matrix[i][j] != INT_MAX)
cout << _matrix[i][j] << " ";
else
cout << "*" << " ";
}
cout << endl;
}
cout << endl;
//打印所有的边:
for (size_t i = 0; i < _matrix.size(); i++)
{
for (size_t j = 0; j < _matrix[i].size(); j++)
{
if (_matrix[i][j] != INT_MAX)
cout << _vertexs[i] << "-" << _vertexs[j] << ":" << _matrix[i][j] << endl;
}
}
}
struct Edge
{
size_t _srci;
size_t _dsti;
W _w;
Edge(size_t srci,size_t dsti,const W& w)
:_srci(srci),_dsti(dsti),_w(w) {}
bool operator>(const Edge& e) const
{
return _w > e._w;
}
};
//从连通图中找最小生成树
W Kruskal(self& minTree)
{
size_t n = _vertexs.size();
minTree._vertexs = _vertexs;
minTree._indexMap = _indexMap;
minTree._matrix.resize(n);
for (int i = 0; i < n; i++)
{
minTree._matrix[i].resize(n, MAX_W);
}
priority_queue<Edge, vector<Edge>, greater<Edge>> minq;
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
//i < j 避免相同的边加入两次
if (i < j && _matrix[i][j] != MAX_W)
{
minq.push(Edge(i, j, _matrix[i][j]));
}
}
}
//选出n-1条边:
int size = 0;
W totalw = W();
UnionFindSet ufs(n);
while (!minq.empty())
{
Edge min = minq.top();
minq.pop();
if (!ufs.InSet(min._srci, min._dsti))
{
minTree._addEdge(min._srci, min._dsti,min._w);
ufs.Union(min._srci, min._dsti);
++size;
totalw += min._w;
}
}
if (size == n - 1)
return totalw;
else
return W();
}
W Prim(self& minTree, const W& src)
{
size_t srci = GetVertexIndex(src);
size_t n = _vertexs.size();
minTree._vertexs = _vertexs;
minTree._indexMap = _indexMap;
minTree._matrix.resize(n);
for (int i = 0; i < n; i++)
{
minTree._matrix[i].resize(n, MAX_W);
}
vector<bool> X(n, false);
vector<bool> Y(n, true);
X[srci] = true;
Y[srci] = false;
priority_queue<Edge, vector<Edge>, greater<Edge>> minq;
for (size_t i = 0; i < n; i++)
{
if (_matrix[srci][i] != MAX_W)
minq.push(Edge(srci, i, _matrix[srci][i]));
}
size_t size = 0;
W totalw = W();
while (!minq.empty())
{
Edge min = minq.top();
minq.pop();
//最小边的目标点也在X集合则构成环
if (X[min._dsti])
{
cout << "构成环:";
cout << _vertexs[min._srci] << "->" << _vertexs[min._dsti] << ":" << min._w << endl;
}
else
{
//添加边:
minTree._addEdge(min._srci, min._dsti, min._w);
cout << _vertexs[min._srci] << "->" << _vertexs[min._dsti] << ":" << min._w << endl;
X[min._dsti] = true;
Y[min._dsti] = false;
++size;
totalw += min._w;
if (size == n - 1)
break;
for (size_t i = 0; i < n; i++)
{
if (_matrix[min._dsti][i] != MAX_W && Y[i])
minq.push(Edge(min._dsti, i, _matrix[min._dsti][i]));
}
}
}
if (size == n - 1)
return totalw;
return W();
}
private:
vector<V> _vertexs; //存储顶点的集合
vector<vector<W>> _matrix; //存储边集合的矩阵
map<V, int> _indexMap;//顶点映射下标
};
void TestGraphMinTree()
{
const char* str = "abcdefghi";
Graph<char, int> g(str, strlen(str));
g.AddEdge('a', 'b', 4);
g.AddEdge('a', 'h', 8);
g.AddEdge('b', 'c', 8);
g.AddEdge('b', 'h', 11);
g.AddEdge('c', 'i', 2);
g.AddEdge('c', 'f', 4);
g.AddEdge('c', 'd', 7);
g.AddEdge('d', 'f', 14);
g.AddEdge('d', 'e', 9);
g.AddEdge('e', 'f', 10);
g.AddEdge('f', 'g', 2);
g.AddEdge('g', 'h', 1);
g.AddEdge('g', 'i', 6);
g.AddEdge('h', 'i', 7);
Graph<char, int> kminTree;
cout << "Kruskal:" << g.Kruskal(kminTree) << endl;
kminTree.Print();
Graph<char, int> pminTree;
cout << "Prim:" << g.Prim(pminTree,'a') << endl;
pminTree.Print();
}
}
int main()
{
matrix::TestGraphMinTree();
return 0;
}到了这里,关于最小生成树—Kruskal算法和Prim算法的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!