2023年美国大学生数学建模竞赛B题重塑马赛马拉的形象解题全过程文档及程序-Toy模板网

这篇具有很好参考价值的文章主要介绍了2023年美国大学生数学建模竞赛B题重塑马赛马拉的形象解题全过程文档及程序。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

2023年美国大学生数学建模竞赛

B题重塑马赛马拉的形象

原题再现：

背景介绍
肯尼亚的野生动物保护区最初主要是为了保护野生动物和其他自然资源而设立的。肯尼亚议会通过了2013年《野生动物保护和管理法》，以提供更公平的资源共享，以及允许替代的、基于社区的管理努力。此后，肯尼亚增加了修正案，以解决立法中的漏洞，提供更明确的治理、财政和对违法者的惩罚。
要求
你的任务是以马赛马拉这个大型野生动物保护区为重点，确定管理公园内外资源的替代方法。具体来说，你应该。
●考虑并推荐当前保护区内不同区域的具体政策和管理策略，这些政策和策略将保护野生动物和其他自然资源，同时也将平衡居住在该地区的人们的利益。这些政策和策略应有助于减轻居住在保护区附近的人们所经历的机会丧失的影响，并尽量减少动物和被保护区吸引的人们之间的负面互动。
●制定并描述一种方法，以确定哪些政策和管理战略将产生最佳结果。你的报告应该讨论如何对你的方法的结果进行排序和比较。一定要包括描述和分析用于预测动物和人之间互动的模型，以及由此对保护区内和周围地区的经济影响。
●鉴于你提出的计划，对你的建议所带来的长期趋势进行预测。分析并提供对可能的长期结果的确定性和影响的估计。你还应该描述你的方法如何适用于其他野生动物管理区。
最后，为肯尼亚旅游和野生动物委员会提供一份两页的非技术性报告，讨论你提出的计划及其对保护区的价值。

整体求解过程概述(摘要)

每年，世界上最壮观的野生动物迁徙，口口相传地称为“马拉河渡口”，发生在肯尼亚的马赛马拉保护区。该保护区最初是为了保护野生动植物和自然资源而建立的。然而，生活在该地区的人民的利益也不容忽视。
在建立所有模型之前，我们对大量数据进行高可靠性的清理和可视化，这对我们后续的指标选择工作有很大帮助。此外，我们精确地定义了“失去的机会”和“消极互动”的模糊概念。
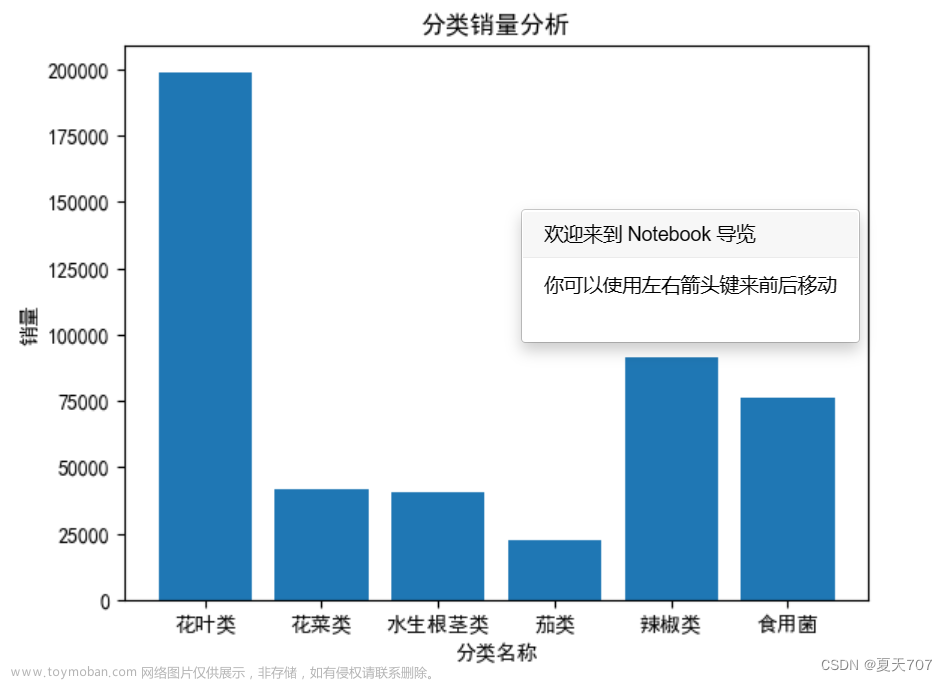
对于问题 1，我们将马赛马拉大致平均分为 36 个网格，以便于建模，同时考虑到其当前的自然资源和野生动物分布。对于每个网格，我们选择建立 4 个功能区之一：野生动物保护区、农业区、狩猎区或旅游区。为了平衡区域内野生动物和人类的利益，我们提出了生态效益和经济效益的概念和计算方法，并将其最大值作为目标函数。我们建立了模型一：基于双目标规划的马赛马拉资源配置战略模型。制约因素是：（1）生态效益的大小制约了功能区的类型;（2）游客数量的限制;（3）居民收入保障等。使用术语，计算出 3 个 seanarios。以场景2为例：建立13个野生动物保护区、13个农区、 2个狩猎区、9个旅游区。

对于问题2，为了确定能够产生最佳结果的管理解决方案，我们开发了模型二：基于Dijkstra的最小相互作用模型和经济影响评价模型。我们指定了四种类型的交互作用，类似于四个功能区域之间的影响关系，并确定有向图中路径的权重。基于从问题 3 的求解中获得的 1 个场景，我们使用改进的 Dijkstra 算法通过分别计算其最短路径来衡量每个场景的交互影响。同时，考虑到马赛马拉地区的经济发展水平，三种情景的经济效益分别为141，274.438美元，154，948.974美元和130，180.760美元（单位：百万）。结果表明，情景2交互性最佳，经济效率最高。因此，方案 2 是最好的。
对于问题3，我们开发了模型三：马赛马拉地区的长期趋势预测模型。我们首先预测了游客的增加，这可能是由于负面的人与动物互动减少造成的。然后，我们拟合了一个二次非线性回归方程来预测2010-2019年肯尼亚旅游收入与游客数量之间的关系，进而预测旅游收入的变化。以COVID-19大流行为例，在检验长期预测结果的准确性时，我们使用t检验并计算出小于0.05的p值，表明COVID-19大流行前后肯尼亚的旅游收入存在显著差异。COVID-19大流行被认为影响了旅游业。由于影响因素丰富，我们的模型具有很强的适应性以及讨论的特殊情况。我们研究了它在黄石国家公园的应用。
最后，对指数权重的敏感性分析表明，我们的模型对它们的变化并不敏感。在讨论了该模型的优势和改进之后，为肯尼亚旅游和野生动物委员会编写了一份关于马赛马拉资源再分配计划及其价值的两页非技术报告。

模型假设：

为了简化问题，我们做出以下基本假设，每个假设都有适当的理由。

假设1：本文中的所有数据来源都是真实可靠的。
理由：我们需要依靠马赛马拉及周边地区的历史数据来分析其在经济、气候和生物多样性方面的趋势。因此，数据的可靠性非常重要。
假设2：未来50年内，马赛马拉及周边地区不会发生重大自然灾害。
理由：地震、泥石流、海啸等自然灾害属于不可抗力因素，我们无法准确预测或量化它们对模型稳定性的影响。
假设3：马赛马拉地区的人与自然平衡不受我们讨论的影响以外的因素的支配。
理由：我们尽可能设想了可能影响问题的相关因素，并给出了几乎不存在其他因素影响的原因。因此，为了简化模型，我们可以做出上述假设。
假设4：对于马赛马拉划分的36个地区，可以假设每个小区域内的环境，经济和其他条件是相同的。
理由：马赛马拉地区分区的合理理想化。假设区域内的条件相同，有助于我们计算相关的收益和成本。
假设5：对于马赛马拉地区部分难以获得的数据，可以用肯尼亚的数据代替。
理由：由于难以获得马赛马拉部分地区的数据，我们不得不替换来自肯尼亚的相关数据，但是，根据已知数据的相似性，我们可以得出结论，这种做法对我们模型准确性的影响在合理的误差范围内。

问题重述：

对于问题1，我们需要考虑是否针对当前保护区的不同区域改进具体的政策和管理策略。在考虑新的政策和管理策略时，我们需要平衡生态效益和经济效益，同时避免对旅游业吸引到保护区的人们产生负面影响。

对于问题 2，我们需要确定哪些策略和管理策略效果最好。我们需要构建一个模型来对 task1 的结果进行排名和比较。排名和比较的原则包括该政策下的动物与人类的互动是否大多是积极的，以及它们是否对保护区内和周围的经济产生积极影响。

对于问题 3，我们需要预测任务 1 中提出的计划对未来发展的影响。我们需要分析相应的政策和管理策略的结果，以及如何将这些管理策略应用于其他自然保护区。

对于问题4，我们需要向肯尼亚旅游和野生动物委员会提供一份非技术性报告。在报告中，我们需要描述我们提出的计划，并分析该计划对马赛马拉保护区的影响和价值。

模型的建立与求解整体论文缩略图

2023年美国大学生数学建模竞赛B题重塑马赛马拉的形象解题全过程文档及程序
文章来源地址https://www.toymoban.com/news/detail-452503.html

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可

部分程序代码：(代码和文档not free)

function [min,path]=dijkstra(w,start,terminal) 
n=size(w,1); label(start)=0; f(start)=start; 
for i=1:n

if i~=start

label(i)=inf;

end

end

%sThe array holds the set of vertices already searched, initialized with only start s(1)=start; u=start;

while length(s)<n for i=1:n

ins=0;

for j=1:length(s)

if i==s(j) ins=1;
if i==s(j) ins=1;

end end

end

%Determine if there are relay vertices that make the distance between them shorter, if so update the distance and update the precursor node

if ins==0

v=i;

if label(v)>(label(u)+w(u,v))

label(v)=(label(u)+w(u,v));

f(v)=u;

end

end

end