SVD分解示例

4月前作者：Longer2048 分类：Toy博客阅读(19) 违法举报

这篇具有很好参考价值的文章主要介绍了SVD分解示例。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

帮助到你了就点个赞吧！

Powered By Longer-站在巨人的肩膀上文章来源地址https://www.toymoban.com/news/detail-452641.html

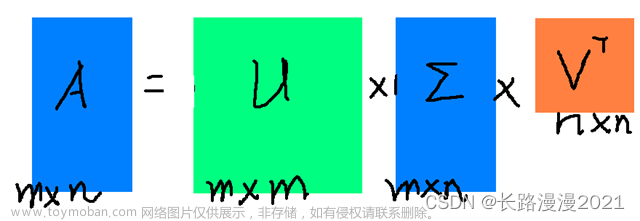
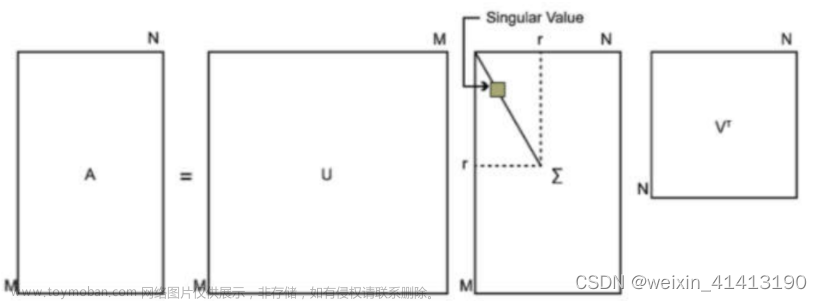
对矩阵A进行SVD分解的公式：。其中A可以不是方阵，是左奇异矩阵，是右奇异矩阵。其中V是的特征向量（注意公式中V有个转置操作），U是的特征向量。是对角阵，对角元素是U、V的共同特征值，例如有三个特征值时：。

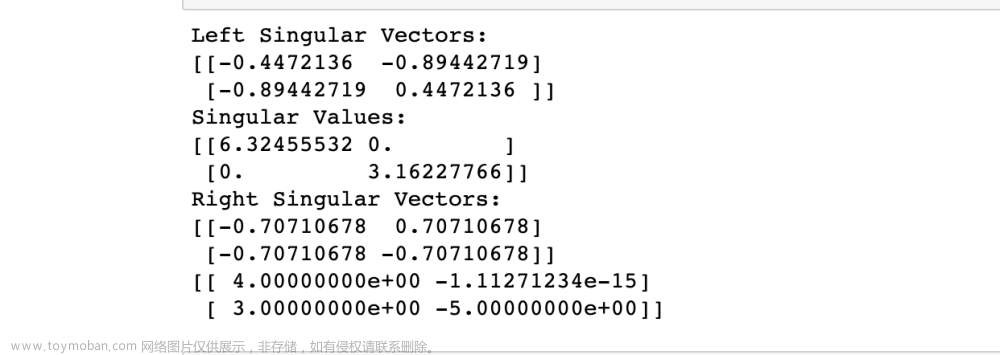
举个简单的例子，对矩阵A进行SVD分解：

从而得到的特征值和特征向量()，右奇异矩阵，：

同时得到的特征值和特征向量()，左奇异矩阵：

因此奇异值：

所以对角阵

至此左奇异矩阵，右奇异矩阵和对角阵都凑齐了，即为：

另外：生成多元具有相关性的随机变量时，也可以使用SVD分解法，详见：多元相关随机变量的生成。

帮助到你了就点个赞吧！

Powered By Longer-站在巨人的肩膀上

到了这里，关于SVD分解示例的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！

分享到：

领支付宝红包赞助服务器费用

时序分解 | MATLAB实现基于SVD奇异值分解的信号分解分量可视化

效果一览基本介绍 SVD分解重构算法，MATLAB程序，奇异值分解 (Singular Value Decomposition)是一种常见的矩阵分解方法，用于将矩阵分解成三个矩阵的乘积。在信号处理中，SVD 可以用于特征提取、信号降维、图像压缩等方面。SVD 的一个重要应用是主成分分析 (PCA)，可以用于提取数

2024年02月11日
浏览(17)
机器学习实战：Python基于SVD奇异值分解进行矩阵分解（八）

1.1 奇异值分解奇异值分解（ Singular Value Decomposition，SVD ）是一种重要的矩阵分解技术，它可以将一个矩阵分解为三个矩阵的乘积，分别为左奇异矩阵、奇异值矩阵和右奇异矩阵。SVD 的原理可以描述如下：对于任意 m × n m times n m × n 的矩阵 A A A ，它的 SVD 分解为： A = U $

2024年02月02日
浏览(26)
矩阵篇（五）-- 特征值分解(EVD)和奇异值分解(SVD)

设 A n × n A_{n times n} A n × n 有 n n n 个线性无关的特征向量 x 1 , … , x n boldsymbol{x}_{1}, ldots, boldsymbol{x}_{n} x 1 , … , x n ，对应特征值分别为 λ 1 , … , λ n lambda_{1}, ldots, lambda_{n} λ 1 , … , λ n A [ x 1 ⋯ x n ] = [ λ 1 x 1 ⋯ λ n x n ] Aleft[begin{array}{lll

2024年02月08日
浏览(20)
数值线性代数：奇异值分解SVD

本文记录计算矩阵奇异值分解SVD的原理与流程。注1：限于研究水平，分析难免不当，欢迎批评指正。设列满秩矩阵，若的特征值为，则称为矩阵的奇异值。设，则存在正交矩阵与，使得其中，，，即为矩阵的奇异值。考虑下述两种情形：情形1：其中，由此可以看出，

2024年02月15日
浏览(14)
Python实现矩阵奇异值分解(SVD)

Python实现矩阵奇异值分解(SVD) 矩阵奇异值分解(Singular Value Decomposition, SVD)是一种重要的矩阵分解方法，可以将一个矩阵分解成三个矩阵的乘积，即 A = U Σ V T A=USigma V^{T} A = U Σ

2024年02月10日
浏览(15)
基于opencv的SVD分解求解变换矩阵

在机器视觉领域，坐标系之间的转换是必不可少的。空间坐标转换的实质是用公共点的两套坐标去推导出两个坐标系之间的转换关系：R（旋转矩阵）和T（平移向量）。其实点云的配准过程就是求解旋转矩阵R和平移向量T，这里记目标函数为：式中，n是匹配点个数，假设其最

2024年02月11日
浏览(12)
t-svd张量分解算法详解

讲解我们张量分解上面经常说的t-svd内容，原论文题目如下： Factorization strategies for third-order tensors 论文链接：link 拥有高中基础水平知识，并且学习了部分矩阵分析内容我们先来规定一些特定的符号，不再在下文重复解释。符号意义 x 标量（就是单纯的任意一个数） x ma

2024年02月03日
浏览(28)
奇异值分解SVD（singular value decomposition）

SVD是一个很有用的矩阵因子化方法。 SVD提出的目的：任何一个 m × n mtimes n m × n 的矩阵都可以当作一个超椭圆（高维空间的椭圆），可以把它们当作单位球体S的像。一个超椭圆可以通过将单位球型在正交方向 u 1 , u 2 , . . . , u m mathbf{u_1},mathbf{u_2},...,mathbf{u_m} u 1 , u 2

2024年02月03日
浏览(11)
SVD，奇异值分解的计算步骤以及实例讲解

奇异值分解（singular value decomposition,SVD）,已经成为矩阵计算中最有用和最有效的工具之一，并且在最小二乘问题、最优化、统计分析、信号与图像处理、系统理论与控制等领域得到广泛应用。首先我们都知道方阵是可以特征值分解的，那么问题来了，如果矩

2024年02月04日
浏览(15)
【机器学习】奇异值分解（SVD）和主成分分析（PCA）

在机器学习（ML）中，一些最重要的线性代数概念是奇异值分解（SVD）和主成分分析（PCA）。收集到所有原始数据后，我们如何发现结构？例如，通过过去 6 天的利率，我们能否了解其构成以发现趋势？对于高维原始数据，这变得更加困难。这就像

2024年02月15日
浏览(21)