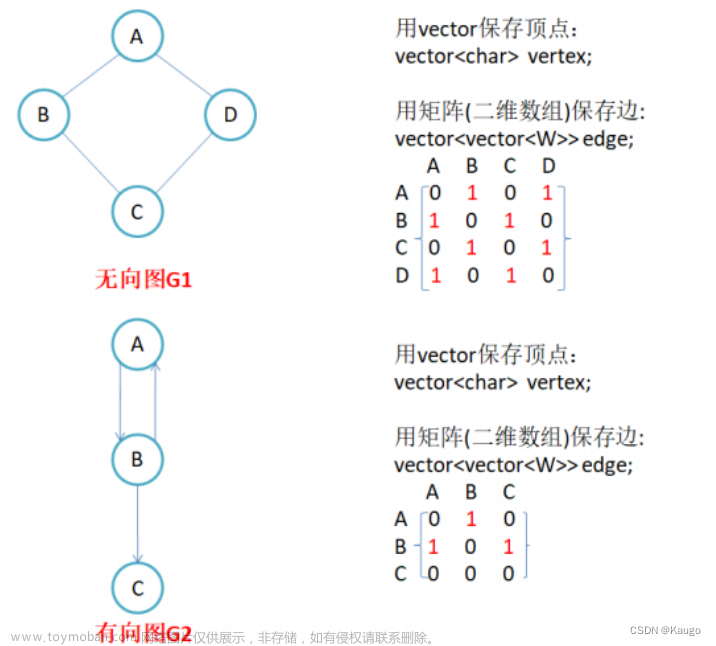
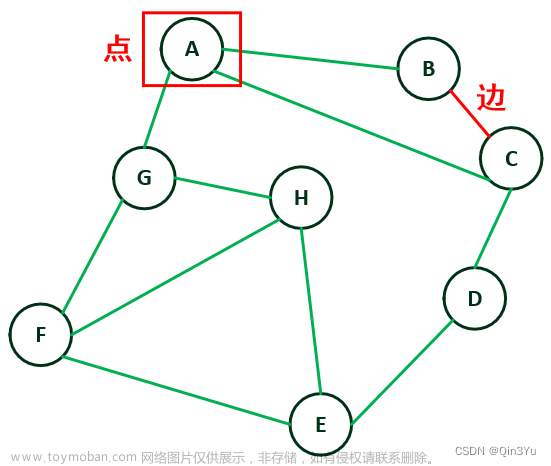
一、邻接矩阵实现无向图
关键点:
1.构建二维数组
2.对应边的位置赋值为1
由于比较简单就直接上代码:
#include<stdio.h>
#include<iostream>
#define maxsize 100
using namespace std;
template <typename T>
class undigraph
{
public:
int vertexnum;//顶点数量
int maxvertex=0;
T data[maxsize];//用来储存各个顶点的数据
int adjmatrix[maxsize][maxsize];//定义邻接矩阵
void createundigraph();
void printadjmatrix();
};
template <typename T>
void undigraph<T>::createundigraph()
{
T tempdata;//临时数据
int adjvertex;
int i=0;
for(;;i++)
{
cout<<"请输入顶点"<<i<<"数据:"<<endl;
cin>>tempdata;
if (tempdata==-1)//如果用户输入数据为-1那么代表输入结束
{
break;
}
data[i]=tempdata;
cout<<"请输入该顶点的相邻顶点:"<<endl;
cin>>adjvertex;
if (adjvertex>=maxvertex)
{
maxvertex=adjvertex+1;//得到顶点的边界值
}
adjmatrix[i][adjvertex]=1;
adjmatrix[adjvertex][i]=1;
}
cout<<"邻接矩阵构建完毕"<<endl;
}
template <typename T>
void undigraph<T>::printadjmatrix()//打印邻接矩阵
{
for (int i = 0; i < maxvertex; i++)
{
for (int j = 0; j < maxvertex; j++)
{
cout<<adjmatrix[i][j]<<" ";
}
cout<<endl;
}
}
int main()
{
undigraph<int> ug;
ug.createundigraph();
ug.printadjmatrix();
return 0;
}二、邻接表实现无向图
个人对邻接表实现无向图的理解如下,仅供参考:
结构组成
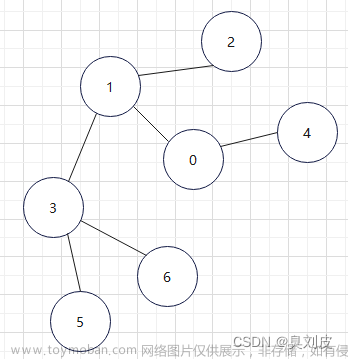
由于无向图的组成是由多个顶点和多条无向边组成的,因此我们可以把它拆分成两个结构,分别是顶点和无向边,又由于我们是使用链式结构进行图的储存的,因此我们可以把图看作是很多条链表组成,每条链表的首个元素(我称之为链表头)正代表了各个顶点,因此就可以得到以下的图:


思考
既然已经分成了两部分,分别是顶点和无向边,那么无向边上需要储存的数据是什么?顶点需要储存的数据是什么?
既然无向边是用来表示两个顶点相连的一条边,而如上图所示,每个链表头就表示了一个顶点,那么无相边上只需要保留三个数据,一个是无向边的权值,一个是连接的另一个顶点(也就是和链表头那个顶点相连的顶点),还有一个就是指向下一条边的指针。
由于无向边不需要储存具体数据,因此具体的数据储存于链表头中,而链表头也需要指向他的第一条边,因此还需要一个指向第一条边的指针。
总结
由上面的思考过程我们可以知道一供有两种数据,分别是点和边,因此我们在编程中就需要创建这两个类,而具体创建无向图所需的数据,如顶点的数量,边的数量等就储存在主类(也就是无向图类)中。
图示

程序执行流程图


getheadlist的流程图我就不给出了,因为只是一个遍历就可以解决的事情,具体可以看后面的代码。文章来源:https://www.toymoban.com/news/detail-452653.html
具体代码
#include<stdio.h>
#include<iostream>
#define maxsize 100
using namespace std;
class linenode//邻接表的主要储存方式就是通过这个边节点
{
public:
//拥有三个属性,一是边上的一个顶点,二是边的权值,三是下一条边
int adjvertex;//顶点
int weight;//边权值
linenode* nextline;//指向下一条边的指针
};
class vertexnode//顶点,这个类主要为链表头数列服务
{
public:
//拥有两个属性,一个是顶点上的数据data,一个是顶点的第一条边
int data;//顶点的数据
linenode* firstline;//指向第一条边的指针
};
class undigraph//无向图
{
public:
//bool visited[maxsize];//访问数组
vertexnode* adjlisthead;//链表头就是各个顶点,因此这个指针指向的是顶点
int vertexnum;//顶点的数量
void createundigraph();
void insertlinklist(int v1,int v2);
int getlisthead(int value);
};
void undigraph::createundigraph()
{
cout<<"进入构造函数"<<endl;
cout<<"请输入顶点数目:"<<endl;
int tempvertexnum=0;
cin>>tempvertexnum;//输入顶点的数量
vertexnum=tempvertexnum;
adjlisthead=new vertexnode[vertexnum];
//得到顶点数量之后就可以利用其创建一个类数组,也就是说adjlisthead通过这一步骤指向了一个大小为顶点数目的类数组
//并且通过这个步骤就可以自动构造vertexnum个类,并且如果要访问这个类数组之中的某个类,只需要通过这个指针来访问
//示例:adjlisthead[0].data //这一步就可以得到创建的第一个类的data
//要创建类数组,首先需要在类内定义一个类指针,然后在外部给这个类指针分配内存,格式如上所示,一旦分配完毕之后就会构造相应数量的类
//并且可以通过这个类指针进行访问
for (int i = 0; i < vertexnum; i++)
{
cout<<"请输入顶点"<<i+1<<"的数据:"<<endl;
cin>>adjlisthead[i].data;//输入顶点的数据
adjlisthead[i].firstline=NULL;//并且初始化每一个顶点指向的边的指针为空
}
cout<<"请输入边的数量:"<<endl;
int linenum;
int v1,v2;
cin>>linenum;
for (int i = 0; i < linenum; i++)
{
cout<<"请输入要相连的两个点:"<<endl;
cin>>v1>>v2;//输入两个相连的顶点
insertlinklist(v1,v2);
insertlinklist(v2,v1);
}
}
void undigraph::insertlinklist(int v1,int v2)
{
int i,j;
i=getlisthead(v1);
j=getlisthead(v2);
linenode* p1;
linenode* p2;
p2=new linenode;
p2->adjvertex=j;
p2->nextline=NULL;
if ((adjlisthead[i].firstline==NULL)||(adjlisthead[i].firstline->adjvertex>j)).
//如果要连接的第一个节点只存在链表头,也就是没有和任何点相连,或者要连接的第一个节点指向的第一条边的顶点比要连接的那个节点序号大
//那么就把要连接的第二个线节点p2插入到中间
{
p2->nextline=adjlisthead[i].firstline;
adjlisthead[i].firstline=p2;
}
else
//否则先将p1初始化为,以他作为链表头的链表的第一条边节点
//循环检查,条件是不为空且对应的边节点的下一条边节点的顶点序号小于要连接的第二个节点的序号(这个序号由链表头数组得来)
{
p1=adjlisthead[i].firstline;
while ((p1->nextline)&&(p1->nextline->adjvertex<j))
{
p1=p1->nextline;//向右遍历
p2->nextline=p1->nextline;//同时更改p2的下一个边节点
p1->nextline=p2;//并将p2所在边界点赋值为p1的下一个边界点
//关键点就是不断的插入并判断序号大小,一旦符合条件就跳出循环,表示连接完毕
}
}
}
int undigraph::getlisthead(int value)
{
int j;
for (j = 0; j < vertexnum; j++)
{
if (adjlisthead[j].data==value)
{
break;
}
}
return j;
}
int main()
{
undigraph ug;
ug.createundigraph();
return 0;
}这是我csdn的第一篇博客,希望大家可以提提建议,如果喜欢的话也可以给我点个赞,本人也是大二在读,有没写好的地方多多指正。文章来源地址https://www.toymoban.com/news/detail-452653.html
到了这里,关于C++数据结构之图的存储结构——邻接矩阵和邻接表实现无向图的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!