****显著性水平:
一个概率值,原假设为真时,拒绝原假设的概率,表示为 alpha 常用取值为0.01, 0.05, 0.10
****什么是P值?
p值是当原假设为真时样本观察结果及更极端结果出现的概率。
如果P值很小,说明这种情况发生的概率很小,如果这种情况还出现了,那么就有理由拒绝原假设。P值越小,拒绝原假设的理由就越充分。
根据选取的检验统计量计算P值,通过P值确定是否拒绝该原假设。
****P值是指在零假设成立的情况下,观察到的检验统计量至少如同观察到的那样极端的概率。它用于假设检验,以确定观察到的数据是否具有统计学显著性。
****P值是具有零假设为真的情况下观察到的效应发生的概率。
****检验中常说的小概率:
在一次试验中,一个几乎不可能发生的事件发生的概率
在一次试验中小概率事件一旦发生,我们就有理由拒绝原假设
小概率由我们事先确定;
****假设检验的基本思想是统计学的 小概率反证法 思想:对于一个小概率事件而言,其互斥事件发生的概率明显远远大于这一小概率事件,可以认为小概率事件在一次试验中不应当发生。因此,可以首先假定需要考察的假设是成立的,然后基于此假设计算从总体中抽样得到样本的概率,如果概率极小,则表明这是一个小概率事件,在一次试验中不会发生,进而推翻原假设。
****假设检验的具体步骤为:1.提出零假设和备择假设;2.构造检验统计量,并找出在零假设成立的情况下,检验统计量服从的分布;3.确定显著性水平、拒绝域以及临界值;4.计算检验统计量和p值;5.决策。
****检验统计量 是根据样本观测结果计算得到的样本统计量,是对零假设和备择假设作出决策的基础。
什么是t检验
t检验(Student’s T Test)比较两个平均值(均值),然后告诉你它们彼此是否有差异。并且,t检验还会告诉你这个差异有没有意义,换句话说,它让你知道这些差异是否可能是偶然发生的。
什么是t分数
t分数是两个组之间的差值与组内差的比值。t分数越大,组间的差异越大。t分数越小,组间的相似度就越大。t分数为3代表这些组是彼此之间的三倍。当你运行t-score时,t值越大,结果越可能重复。
t分数越大,这些组差异越大。
如果t分数越小,这些组越相似的。
什么是T值和P值
“足够大”多大?每个t值都有伴随着一个p值。p值是你的样本数据的结果偶然发生的概率。P值为0%至100%。它们通常写为小数。例如,5%的p值为0.05。低p值好;低假定值是好的;他们指出你的数据不是偶然发生的。例如,p值为0.1意味着实验结果只有1%的可能是碰巧发生的。多数情况下,p值为0.05(5%)表示数据有效。
t检验有哪些类型
t检验有三种主要类型:
1.独立样本t检验:比较两组平均值的方法。
2.配对样本t检验:比较同一组中不同时间(例如,相隔一年)平均值的方法。
3.单一样本t检验:检验单个组的平均值对照一个已知的平均值。
三、假设检验
统计假设检验(Hypothesis Test):事先对总体的参数或者分布做一个假设(刚才的例子我们就假设 p=0.5 的二项式分布),然后基于已有的样本数据去判断这个假设是否合理。即样本和总体假设之间的不同是纯属机会变异(因为随机性误差导致的不同),还是两者确实不同。常用的假设检验方法有 t- 检验法、x2 检验法(卡方检验)、F- 检验法等
基本思想:
1、从样本推断整体
2、通过反证法推断假设是否成立(假设整体满足分布,出现这个样本分布的概率大不大,如果概率非常小,那么假设不成立)
3、小概率事件在一次实验中基本不会发生(低于50%就不会发生,那么50%是我们选择的值,如果比较严格的话,可以把这个值降到1%)
4、不轻易拒绝原假设
5、通过显著性水平定义小概率事件不可能发生的概率
6、全称命题只能被否定而不能被证明(通过当前的样本我希望做一个假设,用分布的情况来推翻这个假设不成立,但是很难证明它成立)
一、假设检验
统计假设检验:事先对总体的参数或者分布做一个假设,然后基于已有的样本数据去判断这个假设是否合理。即样本和总体假设之间的不同是纯属机会变异(因为随机性误差导致的不同),还是两者确实不同。常用的假设检验方法有 t- 检验法,x2 检验法(卡方检验)、F- 检验法等。
基本思想:
1、从样本推断整体
2、通过反证法推断假设是否成立
3、小概率事件在一次实验中基本不会发生
4、不轻易拒绝原假设
5、通过显著性水平定义小概率事件不可能发生的概率
6、全称命题只能被定义而不能被证明(所谓全称命题是指一切全部等等不太容易一个一个验证的,没有办法证实,只要找到一个部分,就能证明这个命题错误;但是要证明这个命题是正确,就很费劲了)
三、原理
1、原假设怎样设定;(相等,不相等,差异性)
2、提高,增加,降低如何选择;
3、原假设是希望收集数据推翻的,如果假设成立(当前的事情发生的概率大小,当然我们希望当前假设将原假设推翻)。如果证据无法推翻原假设,那就既证明原假设成立,也不能证明原假设不成立。
因为原假设备被拒绝,如果出错的话,只能犯弃真错误,而犯弃真错误的概率已经被规定的显著性水平所控制了。这样对统计者来说更容易控制,将错误影响降到最小。
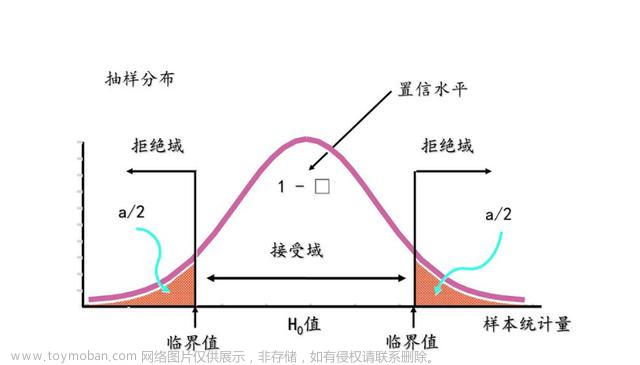
显著性水平
显著性水平是指当原假设实际上正确时,检验统计量落在拒绝域的概率,简单理解就是犯弃真错误的概率。这个值是我们做假设检验之前统计者根据业务情况定好的。
显著性水平α越小,犯第I类错误的概率自然越小,一般取值:0.01、0.05、0.1等。
当给定了检验的显著水平a=0.05时,进行双侧检验的Z值为1.96。
当给定了检验的显著水平a=0.01时,进行双侧检验的Z值为2.58。
当给定了检验的显著水平a=0.05时,进行单侧检验的Z值为1.645。
当给定了检验的显著水平a=0.01时,进行单侧检验的Z值为2.33。
检验统计量:据以对原假设和备择假设作出决策的某个样本统计量,称为检验统计量。
拒绝域: 拒绝域是由显著性水平围成的区域。
拒绝域的功能主要用来判断假设检验是否拒绝原假设的。如果样本观测计算出来的检验统计量的具体数值落在拒绝域内,就拒绝原假设,否则不拒绝原假设。给定显著性水平α后,查表就可以得到具体临界值,将检验统计量与临界值进行比较,判断是否拒绝原假设。
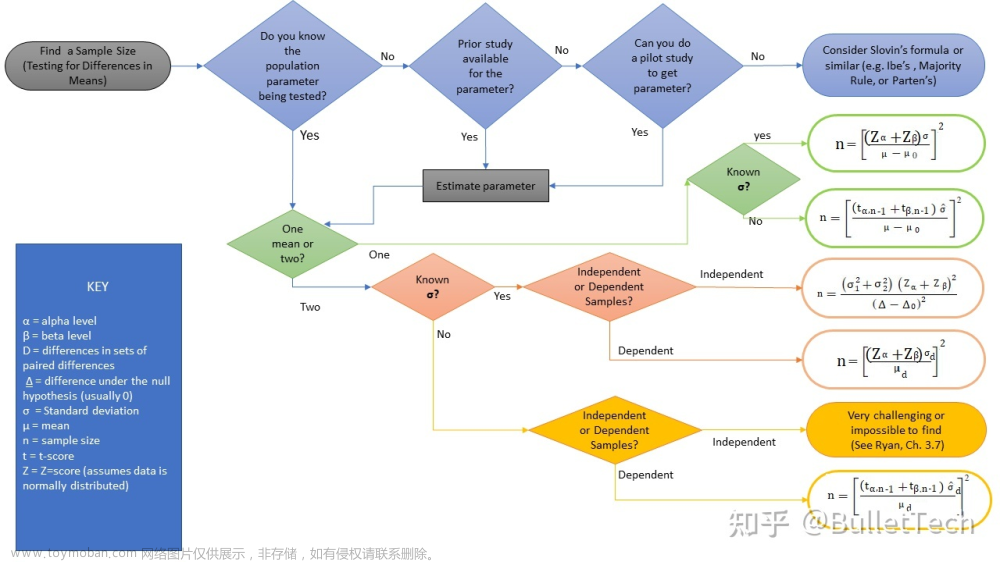
假设检验步骤
提出原假设与备择假设;
从所研究总体中出抽取一个随机样本;
构造检验统计量;
根据显著性水平确定拒绝域临界值;
计算检验统计量与临界值进行比较。
两种假设检验
假设检验根据业务数据分为两种:一个总体参数的假设检验和两个总体参数的假设检验。
一个总体参数的假设检验,即只有一个总体的假设检验。
一、T 检验:
根据研究设计,t 检验有三种形式:
1.单个样本的检验:
用来比较一组数据的平均值和一个数值有无差异。例如,你选取了 5 个人,测定了他们的身高,要看这五个人的身高平均值是否高于、低于还是等于 1.70 m, 就需要用这个检验方法。
2.配对样本均数 t 检验(非独立两样本均数 t 检验)
用来看一组样本在处理前后的平均值有无差异。比如,你选取了 5 个人,分别在饭前和饭后测量了他们的体重,想检测吃饭对他们的体重有无影响,就需要用这个 t 检验。
3.两个独立样本均数 t 检验
用来看两组数据的平均值有无差异。比如,你选取了 5 男 5 女,想看男女之间身高有无差异,这样,男的一组,女的一组,这两个组之间的身高平均值的大小比较可用这种方法。
二、单个样本 t 检验
又称单样本均数 t 检验( one sample test ),适用于样本均数与已知总体均数 μ0 的比较,目的是检验样本均数所代表的总体均数是 μ 否与已知总体均数 μ0 有差别。
已知总体均数 μ0 一般为标准值、理论值或经大量观察得到的较稳定的指标值。
应用条件。总体标准 a 未知的小样
本资料,且服从正态分布
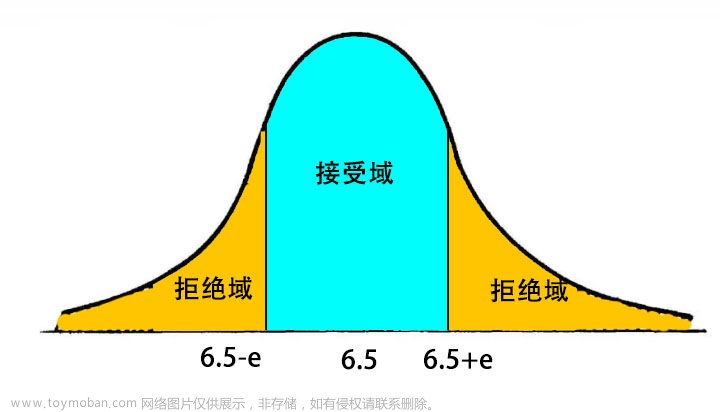
双边检验
最常见,应用于只是简单探究“是否存在差异”的研究问题。
单边检验
适用于探究“是否显著高于”或者“显著低于”的研究问题。
T检验和F检验的关系
t检验过程,是对两样本均数(mean)差别的显著性进行检验。惟t检验须知道两个总体的方差(Variances)是否相等;t检验值的计算会因方差是否相等而有所不同。也就是说,t检验须视乎方差齐性(Equality of Variances)结果。所以,SPSS在进行t-test for Equality of Means的同时,也要做Levene's Test for Equality of Variances 。
T检验是用来比较两个均值之间是否有显著差异的一种检验方法。
T检验是比较两个均值差异的,不同种类T检验的差别其实在于均值的计算差异。
1.单样本T检验stats.ttest_1samp(data,u)
单样本T检验是用来检验一组样本的均值A与一个已知的均值B之间是否有差异。均值A是通过一组样本算出来的,均值B是已知的一个具体的值。
以往通过大规模调查已知某地新生儿出生体重为 3.30 kg .从该地难产儿中随机抽收35 名新生儿,平均出生体重为 3.42 kg ,标准差为 0.40 kg ,问该地难产儿出生体重是否与一般新生儿体重不同?
建立检验假设,确定检验水准
H0: μ=μ0
H1: μ≠ μ0
α=0.05
●计算检验统计量
强调自由度,自由度表示在样本中,可以自由变化的个数。
现样本中已取 35 个,已知均值,假设前 34 个人都已定下并可随机取,第 35 个就不可以随机选,为保证均值不变,第 35 个人一定是固定值的。
本例自由度 v=n-1=35-1=34,查表得得 t0.05/2=2.032。因为 t< t0.05/2. 故 P>0.05. 按 α=0.05 水准,不拒绝 H0, 差别无统计学意义,尚不能认为该地难产儿与一般新生儿平均出生体重不同。
2.双样本T检验stats.ttest_ind(data1,data2)
双样本T检验是用来检验两组样本的均值之间是否有差异。两个均值都是根据样本算出来的。
3.配对样本T检验stats.ttest_rel(data1,data2)
配对样本T检验与双样本T检验有点类似,也是用来检验两组样本的均值差异,只不过普通双样本T检验中的样本是乱序的,而配对样本T检验中的样本是一一对应的。总而言之,就是具有相同属性的数据之间进行相比,而不是混合总体进行相比。
---------
四、配对样本均数t检验:
简称配对 t 检验( paired t test ),又称非独立两样本均数 t 检验,适用于配对设计计量资料均数的比较。
配对设计( paired design )是将受试对象按某些特征相近的原则配成对子,每对中的两个个体随机地给予两种处理
配对样本均数 t 检验原理:关注的是差异值。
配对设计的资料具有对子内数据一 一 对应的特征,研究者应关心是对子的效应差值而不是各自的效应值。
进行配对 t 检验时,首选应计算各对数据间的差值 d,将 d 作为变量计算均数。
配对样本 t 检验的基本原理是假设两种处理的效应相同,理论上差值 d 的总体均数 μd 为 0, 现有的不等于 0 差值样本均数可以来自 μd= 0 的总体,也可以来 ud≠0 的总体。
可将该检验理解为差值样本均数与已知总体均数 pd (μd = 0) 比较的单样本检验,其检验统计量为:
P(AB)与P(A∩B)有什么区别
如果有两个圆,有一部分相交。那P(AB)就是A与B的总数减相交部分的值,而P(A∩B)求的就是相交部分的值。
P(AB)表示P(A∩B)AB同时发生的概率
P(A∪B)表示AB至少有一个发生的概率
1.基于偏度和峰度的假设检验
基于偏度-峰度的检验是利用了正态分布偏度(3阶矩)和峰度(4阶矩)都为0的特点。
如果样本数据能满足偏度和峰度均为0的假设,则可以认为总体服从正态分布。
由于该检验是基于偏度检验和峰度检验的,样本数量需要8个以上。
以下normaltest函数就使用该原理进行正态分布检验。
scipy.stats.normaltest(X)
该函数输出两个结果,第一个为检验统计量,第二个为p值。如果p值大于0.05(常用显著水平)即可认定总体服从正态分布。
使用偏度和峰度拟合优度检验的还有Jarque–Bera检验法。
S为偏度,K为峰度,n为样本数或自由度
同样,Jarque–Bera检验样本数量也需要8个以上。其使用方法如下:
scipy.stats.self_JBtest(X)
该函数输出两个结果,第一个为检验统计量,第二个为p值。如果p值大于0.05(常用显著水平)即可认定总体服从正态分布。
K-S检验原理
KS检验与其他方法不同是KS检验不需要知道数据的分布情况,是一种非参数检验方法,理论上可以检验任何一种分布情况(不限于正态分布检验)。当然付出的代价就是灵敏度没有专门针对某种分布的检验方法高(比如上面的normaltest)。另外,由于大多数KS检验软件在实现是都用大样本近似公式,因此KS算法更适合大样本(300以上)检验。
以下方法就是使用KS检验进行正态分布检验:
kstest(X,"norm")
f检验
T检验和F检验的由来:为了确定从样本中的统计结果推论到总体时所犯错的概率。
F检验又叫做联合假设检验,也称方差比率检验、方差齐性检验。是由英国统计学家Fisher提出。
通过比较两组数据的方差,以确定他们的精密度是否有显著性差异。
t检验
T检验,也称student t检验,主要用户样本含量较小,总体标准差未知的正态分布。
t检验是用t分布理论来推论差异发生的概率,从而比较两个平均数的差异是否显著。
t检验分为单总体检验和双总体检验。
单总体t检验是检验一个样本平均数与一个已知的总体平均数的差异是否显著。
当总体分布是正态分布,如总体标准差未知且样本容量小于30,那么样本平均数与总体平均数的离差统计量呈t分布。文章来源:https://www.toymoban.com/news/detail-453024.html
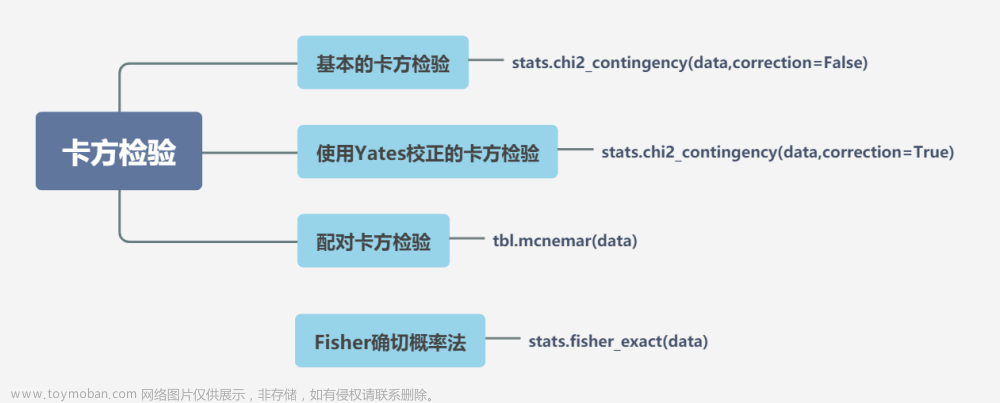
卡方检验
卡方检验就是统计样本的实际观测值与理论推断值之间的偏离程度,实际观测值与理论推断值之间的偏离程度就决定卡方值的大小,卡方值越大,越不符合;卡方值越小,偏差越小,越趋于符合,若两个值完全相等时,卡方值就为0,表明理论值完全符合。文章来源地址https://www.toymoban.com/news/detail-453024.html
到了这里,关于假设检验/T检验/F检验/Z检验/卡方检验的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!