遗传算法五大基本要素——参数编码、群体设定-Toy模板网

这篇具有很好参考价值的文章主要介绍了遗传算法五大基本要素——参数编码、群体设定。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

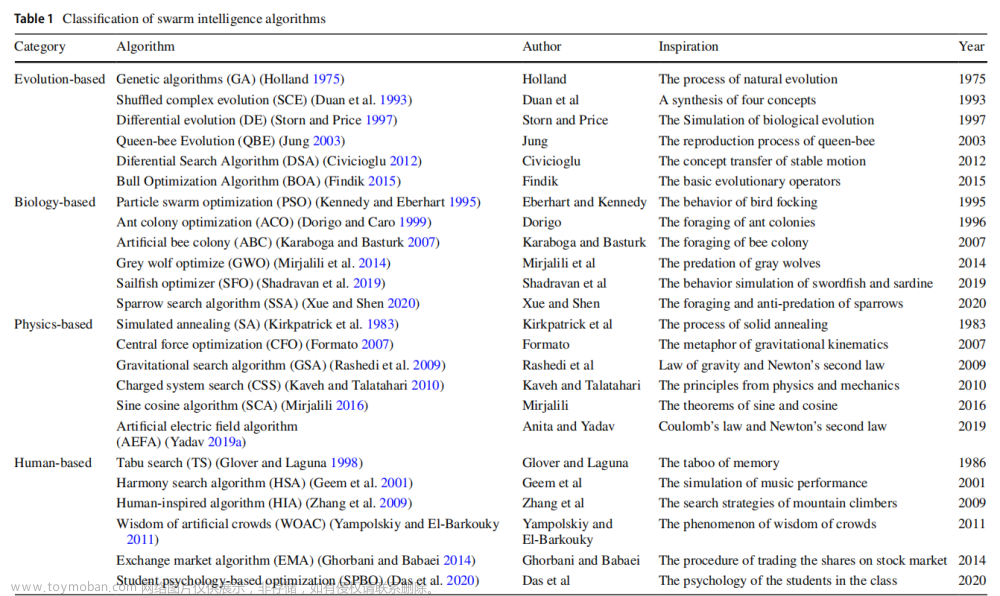
遗传算法主要借用生物进化中的“适者生存”的规律。

遗传算法包括两个数据转换操作，一个是从表现型到基因型的转换，将搜索空间中的参数或解转化成遗传空间中的染色体或者个体，这个过程叫做编码（coding）。另一个就是从基因型到变现型的转换，即将个体转换成搜索空间中的参数，这个过程叫做解码（decode）。

遗传算法中包含了五个基本要素：参数编码，初始群体的设定，适应度函数的设计；遗传操作设计和控制参数设定。

由于遗传算法不能直接处理问题空间的参数，因此，必须通过编码将要求解的问题表示成遗传空间的染色体或者个体。它们由基因按一定的结构组成。由于遗传算法的健壮性，对编码的要求并不苛刻。对一个具体的应用问题如何编码是应用遗传算法的首要问题，也是遗传算法应用的难点。事实上，还不存在一种通用的编码方法，特殊的问题往往采用特殊的方法。

1、编码

1.1 位串编码

将问题空间的参数编码为一维排列的染色体的方法，称为一维染色体编码方法。一维染色体编码中最常用的符号集是二值符号集 ${0，1\}$ ，即采用二进制编码（Binary Encoding）。

（1）二进制编码
二进制编码是用若干二进制数表示一个个体，将原问题的解空间映射到位串空间 $B=\{0，1\}$ 上，然后在位串空间上进来遗传操作。<>/font

优点：二进制编码类似于生物染色体的组成，从而使算法易于用生物遗传理论来解释，并使得遗传操作若交叉、变异等很容易实现。另外，采用二进制编码时，算法处理的模式数最多。

缺点：
①相邻整数的二进制编码可能具有较大的Hamming举例。例如，15和16的二进制表示为01111和10000，因此，算法要从15改进到16则必须改变所有的位。这种缺陷造成了Hamming悬崖（Hamming Cliffs），将降低遗传算子的搜索效率。
②二进制编码时，一般要先给出求解的精度。但求解的精度确定后，就很难在算法执行的过程中进行调整，这就是算法缺乏微调（fine-tuning）的功能。若在算法一开始就选择较高的精度，那么串长就很大，这样也会降低算法的效率。
③在求解高维优化问题的时候，二进制编码串将非常长，从而使得算法的搜索效率很低。

（2）Gray编码
$G r a y$ 编码是将二进制编码通过一个变换进行转换得到的编码。
设二进制串 $β_1β_2...β_n>$ 对应 $G r a y$ 串 $γ_1γ_2...γ_n>$ ，则从二进制编码到 $G r a y$ 编码的变换为：
$γ_k= \begin{cases} β_1,\quad k=1\\ β_{k-1}\bigoplus β_k, \quad k>1 \end{cases} \tag{1}$

上式子（1）中， $\bigoplus$ 表示摸2的加法，也就是异或运算，不同为1，相同为0。

举个例子说明一下：
假设有一个二进制编码串 $10110)_2$ ，那么我们将它转化为Gray编码后为 $11101)_{Gray}$ 。

从一个Gray串到二进制串的变换为：
$β_k=\displaystyle \sum^{k}_{i=1}{γ_i(mod2)}= \begin{cases} γ_1,\quad k=1\\ β_{k-1}\bigoplus γ_k, \quad k>1 \end{cases} \tag{2}$
举个例子说明一下：
假设有一个Gray编码串 $01001)_{Gray}$ ，将其转化为二进制编码串后为 $01110)_2$ 。