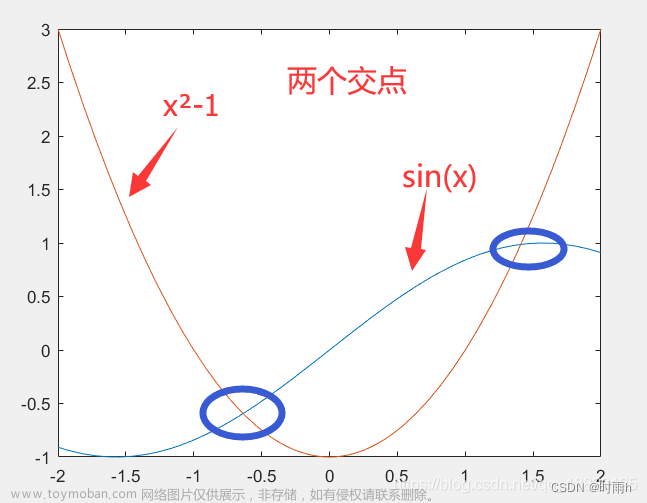
在之前的文章中,我们写出了单模光纤的特征方程以及对应的导波模式
这里我们在MATLAB中求解特征方程并表示出几个归一化参数的变化曲线
用到的公式是单模光纤导波模式的特征方程:
clear
close all
tic
Vmax = 10;
N =100;
for j =1:N
V(j) = j/N*Vmax;
Vtemp = V(j);
Utemp = NaN;
i = 0;
while (isnan(Utemp) && i<N+1)
init =Vtemp*(i+1)/N-1e-16;
try
Utemp = fzero(@(Utemp) ...
besselj(0,Utemp)/(Utemp*besselj(1,Utemp)) - ...
besselk(0,sqrt(Vtemp^2-Utemp^2))/ ...
(sqrt(Vtemp^2-Utemp^2)*besselk(1,sqrt(Vtemp^2-Utemp^2))),init);
catch
end
i = i+1;
end
U(j) = abs(Utemp);
end
W = sqrt(V.^2-U.^2);
Ymax = ceil(max([U,W]));
figure
subplot(1,2,1)
plot(V,U,'r');
axis equal
axis([0 Vmax 0 Ymax])
xlabel('v')
ylabel('u')
title('Lp_{01} v-u')
subplot(1,2,2)
plot(V,W,'r');
axis equal
axis([0 Vmax 0 Ymax])
xlabel('v')
ylabel('w')
title('Lp_{01} v-w')
toc
fzero函数能求解fun(x) = 0 的点 x。
使用方式:
x = fzero(fun,x0)其中x0表示初始值
我们从0-10之间选取了N(100)个点,对于每一个点都有一个Vtemp与之对应
对于每一个确定的Vtemp,特征方程都有一个Utemp与之对应
结果如下:

try catch语句在java中常见于抛出错误
在预见到会产生错误的前提下,把可能引发异常的语句封装在 try 语句块中,用以捕获可能发生的异常。
catch 语句会依据所拋出异常对象的类型进行捕获,并处理。
处理之后,程序会跳过 try 语句块中剩余的语句,转到 catch 语句块后面的第一条语句开始执行。
如果 try 语句块中没有异常发生,那么 try 块正常结束,后面的 catch 语句块被跳过,程序将从 catch 语句块后的第一条语句开始执行。
ceil函数是取整函数,将输入参数的每个元素四舍五入到大于或等于该元素的最接近整数。这里用来规划坐标轴的范围
代码的输出结果就是单模光纤UVW三个元素之间的关系,我们可以在命令行窗口看到具体的数值结果:
[V' U' W']截取前一段来观察:

在V很小时,U和W没有数值解,也就是不存在合适的U和W形成导波模式
在曲线的起始端,对应的数值分别为Vc和Uc
随着V不断增加,U和W都增大,但是,W的增加近似于线性(在V较大的情况下),U的增加趋近于一个有限值
我们可以用多项式拟合得到近似的直线,并和通过特征方程求解的结果作对比:
NN = 15:24
x = V(NN);
y = W(NN);
p = polyfit(x,y,1);
f = polyval(p,x);
maxerr = max(y-f)
figure
plot(x,y,'o',x,f,'-')
xlabel('v')
ylabel('w')polyfit函数用于拟合函数,返回次数为 n 的多项式 p(x) 的系数,该阶数是 y 中数据的最佳拟合(基于最小二乘指标)。p 中的系数按降幂排列,p 的长度为 n+1
这里我们设置阶数为1,也就是直线拟合
结果如下:

polyval函数计算多项式 p 在 x 的每个点处的值。参数 p 是长度为 n+1 的向量,其元素是 n 次多项式的系数(降幂排序)
通过这两个函数组合,我们得到了拟合直线的表达式以及拟合直线的在对应点的结果
在命令行窗口读出最大的误差,可以看到最大的误差是数量级。文章来源:https://www.toymoban.com/news/detail-453181.html
参考《高等光学仿真——光波导、激光》文章来源地址https://www.toymoban.com/news/detail-453181.html
到了这里,关于单模光纤的特征方程以及MATLAB求解的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!