结合实例，直观理解正态分布、卡方分布、t分布、F分布和对应的Z检验、卡方检验、t检验、F检验-Toy模板网

这篇具有很好参考价值的文章主要介绍了结合实例，直观理解正态分布、卡方分布、t分布、F分布和对应的Z检验、卡方检验、t检验、F检验。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

1 正态分布与Z检验

1.1 理论

Z检验的目的是为了验证：已知一个总体服从均值，方差的正态分布，现在有一些样本，这些样本所代表的总体的均值是否为。

则构建一个统计量Z，

（1）

式中，为样本均值，为总体均值，为总体方差，n为样本数量。

若零假设（null hypothesis）成立，即：样本所代表的总体的均值为，则Z服从N(0, 1)。换一种说法就是统计量Z落在下图所示的标准正态分布概率密度函数的大概率区间，也就是白色区域所对应的横轴范围。

结合实例，直观理解正态分布、卡方分布、t分布、F分布和对应的Z检验、卡方检验、t检验、F检验

若Z落在阴影范围所对应的横轴区域，则假设不成立，阴影范围的选取与给定的显著性水平有关。

1.2 应用

工厂老板宣称生产的零件符合正态分布，质检部门抽检了100个样本，那么这些样本所代表的全部零件的均值，是否跟老板所说的正态分布均值一致。这个问题就可以通过Z检验验证，计算样本均值，将样本均值和样本数量代入式（1），看Z值落在横轴的什么区域，白色区域检验合格，黑色区域检验不合格。

2 卡方分布和卡方检验

2.1 自由度的概念

在讲卡方分布前，先要理解样本的自由度。举例说明：一个列表中有10个数字，我告诉你，这10个数字你可以随便写，那么这个列表中10个数字都是“自由的”，有10个自由度。如果我告诉你，这个列表的平均值是5，那么你前9个值你可以随便写，第10个数是固定的，因为必须满足我给定的平均值，这样一来，这个列表的自由度就是9了。

上面是一维的情况，如果推广到二维，看下面这个例子。

	化妆	不化妆	总数
男			100
女			100
总数	90	110

你调查了男生、女生各100人的化妆情况，上面四个空着的格子里，你只能随便写一个，剩下的三个必须根据总数来计算，所以这个例子中，四个空着的格子是4个样本，但是只有一个样本是“自由”的，所以自由度为1。自由度的计算公式：（行数 - 1）*（列数 - 1）

更加详细的自由度解释，参见这边文章：用可视化思维解读统计自由度 - 简书

2.2 卡方分布

卡方分布定义如下

结合实例，直观理解正态分布、卡方分布、t分布、F分布和对应的Z检验、卡方检验、t检验、F检验

2.3 卡方检验

卡方检验的目的是为了验证。两个事物之间是否有关系，还是拿自由度那里提到的男女化妆比例的例子来讲。现在想研究男女性别和是否化妆，这两件事是否相关。

假定不相关（这个就是零假设），也就是说，化妆和不化妆的人群中，男女所占的比例是相同的。在零假设中，样本的标准值就是下面这样：

	化妆	不化妆	总数
男	45	55	100
女	45	55	100
总数	90	110

随机抽样的样本结果如下

	化妆	不化妆	总数
男	X1	X2	100
女	X3	X4	100
总数	90	110

X1、X2、X3、X4为4个抽样样本，其数值分别为5、95、85、15。

构建如下式所示的一个统计量：

（2）

式中，表示第i个样本，表示第i个样本所对应的零假设值，k为样本数量

如果零假设成立，这个统计量服从自由度为n的卡方分布，化妆问题中，自由度为1，即自由度为1的卡方分布。

把样本数据代入式（2），发现其值落在了卡方分布的概率密度函数的小概率区间（与Z检验的原理类似），所以拒绝原假设。

2.4 卡方检验与卡方分布的关系

有读者看到这里会有疑问，为什么式（2）所构建的统计量服从卡方分布？

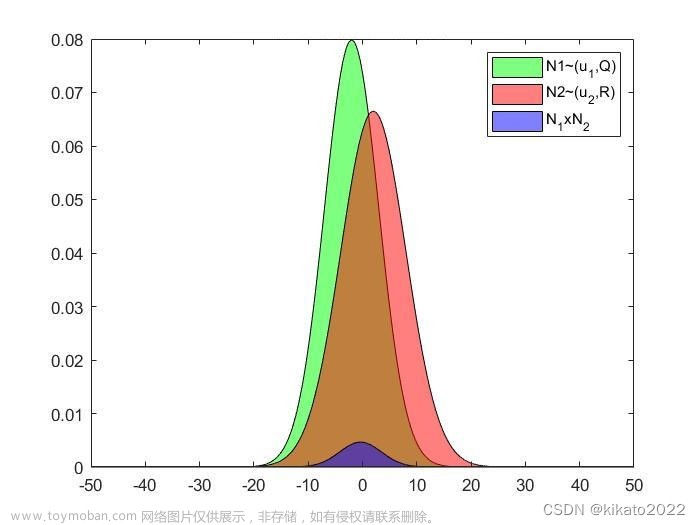
因为服从正态分布，也服从正态分布（正态分布的样本减去常数再除一个常数还服从正态分布），所以那个统计量就服从卡方分布啦，就是卡方分布的定义嘛！

这里再说明一个问题，为什么是服从正态分布的？

原假设中男性化妆和不化妆啊的概率为50%，那么100个男性中化妆的男性数量就满足正态分布了，就像扔硬币的正反面，下面的python代码直观给出了图像

import random
import matplotlib.pyplot as plt
import pandas as pd


plt.rcParams['font.sans-serif'] = ['SimHei']  # 防止中文标签乱码，还有通过导入字体文件的方法
plt.rcParams['axes.unicode_minus'] = False


def toss():
    # 1正面朝上
    return random.randint(0, 1)


def toss_100_times():
    # 掷100次硬币正面朝上的次数
    times = 0
    for i in range(100):
        times += toss()

    return times


if __name__ == "__main__":
    result = []
    for i in range(1000):
        result.append(toss_100_times())

    count = pd.value_counts(result)
    count = pd.DataFrame(count)
    count = count.sort_index(ascending=True)

    labels = list(count.index)
    data = list(count.iloc[:, 0])

    plt.bar(range(len(data)), data)
    plt.xticks(range(len(data)), labels)
    plt.xlabel("100次投掷中正面朝上的硬币数")
    plt.ylabel("频次")
    plt.show()

    print("done")

结合实例，直观理解正态分布、卡方分布、t分布、F分布和对应的Z检验、卡方检验、t检验、F检验