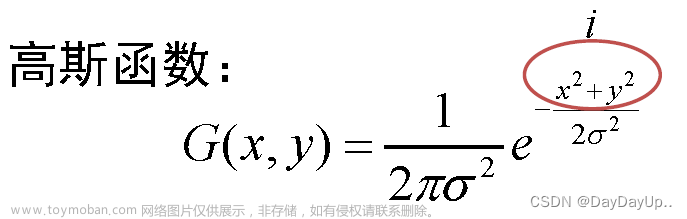常用图像卷积核类型小结-Toy模板网

这篇具有很好参考价值的文章主要介绍了常用图像卷积核类型小结。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

低通滤波器：

均值滤波

高斯滤波

高通滤波器：

锐化卷积核

一阶微分算子

Prewitt算子

Sobel算子

二阶微分算子

Laplace算子

对比:

LoG算子

基本理论

DoG算子

基本理论

高斯模糊代码

DOG代码

卷积操作的主要目的就是对图像进行降维以及特征提取；

1.卷积核往往是行数和列数均为奇数的矩阵，这样中心较好定位；

2.卷积核元素的总和体现出输出的亮度，若元素总和为1，卷积后的图像与原图像亮度基本一致；若元素总和为0，则卷积后的图像基本上是黑色，其中较亮的部分往往就是提取出图像的某种特征；

3.滤波实际上就是Same模式的卷积操作，也就是说滤波后图像的大小不变，各种滤镜和照片的风格化就是使用不同的滤波器对图像进行操作。因此卷积核、滤波器本质上都是一个东西；

4.高通滤波器（High Pass Filter, HPF）表示仅允许图像中高频部分（即图片中变化较剧烈的部分）通过，往往用于对图像进行锐化处理、增强图像中物体边缘等。如Sobel算子、Prewitt算子、锐化滤波器等；

5.低通滤波器（Low Pass Filter, LPF）表示仅允许图像中低频部分（即图片中变化较平缓的部分）通过，往往用于对图像进行模糊/平滑处理、消除噪点等。如高斯滤波器、均值滤波器等；

本文在此将常用的卷积核及其对应的意义总结记录一下，以便随时复习。

低通滤波器：

均值滤波

特点：滤波器中元素之和为1，输出亮度与输入基本一致；
均为低通滤波器，主要用于图像模糊/平滑处理、消除噪点；
核越大，模糊程度越大；

其中均值滤波器从名字就可以看出，每个元素值都一样，是卷积核元素个数的倒数，这样每个输出像素就是其周围像素的均值。一个3 × 3 的均值滤波器如下所示：

常用图像卷积核类型小结

高斯滤波

特点：滤波器中元素之和为1，输出亮度与输入基本一致；
均为低通滤波器，主要用于图像模糊/平滑处理、消除噪点；
核越大，模糊程度越大；

高斯滤波器虽然元素总和也为1，但每个位置的权重不一样，权重在行和列上的分布均服从高斯分布，故称高斯滤波器。高斯分布的标准差越大，则模糊程度越大。一个3 × 3 标准差为1的高斯滤波器如下所示：
常用图像卷积核类型小结
高斯和均值滤波器实例

常用图像卷积核类型小结

这两个滤波器主要作用均为模糊图像，或在图像预处理中消除图像中的噪点：

高通滤波器：

锐化卷积核

概念：
锐化卷积核从名字就可以看出，主要作用就是对图片进行锐化操作，也就是让图像的边缘更加锐利。图像的边缘往往就是变化较大的地方，也就是图像的高频部分，因此锐化卷积核就是一种高通滤波器。一个3 × 3的锐化卷积核如下所示：

常用图像卷积核类型小结

可见该卷积核就是计算中心位置像素与周围像素的差值，差值越大则表示该元素附近的变化越大（频率越大），输出值也就越大，因此是高频滤波器的一种。锐化卷积核元素总和如果是0，则有提取图像边缘信息的效果。

锐化卷积核示例
锐化卷积核作用为突出图像中物体的边缘，相当于给物体描边：

常用图像卷积核类型小结

一阶微分算子

概念
图像中物体的边缘往往就是变化较为剧烈的部分（高频部分），对于一个函数来说，变化越剧烈的地方，对应的导数的绝对值也就越大。图像就是一种二元函数，f ( x , y )表示( x , y ))处像素的值，因此导数除了大小，还有方向。那么求图像在某方向上的一阶导数（或称图像的梯度），也就可以反映出图像在该处的变化程度，变化程度越快，在该方向的垂直方向可能就存在物体的边缘。

一阶微分算子可以计算出某个方向上物体的边缘

但往往对噪声较为敏感，且边缘检测敏感度依赖于物体的大小。

Prewitt算子

Prewitt算子就是对图像进行差分来近似对图像的某个部分求一阶导数。Prewitt算子适合用来识别噪声较多、灰度渐变的图像常用图像卷积核类型小结

常用图像卷积核类型小结

例如像素点P5处 x 和 y 方向上的梯度大小 g_x 和 g_y 分别计算为

常用图像卷积核类型小结

# -*- coding: utf-8 -*-
import cv2
import numpy as np
import matplotlib.pyplot as plt

# 读取图像
img = cv2.imread('C:/Users/123/Pictures/66.png')
img_RGB = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)

# 灰度化处理图像
grayImage = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)

# Prewitt算子
kernelx = np.array([[1, 1, 1], [0, 0, 0], [-1, -1, -1]], dtype=int)
kernely = np.array([[-1, 0, 1], [-1, 0, 1], [-1, 0, 1]], dtype=int)
x = cv2.filter2D(grayImage, cv2.CV_16S, kernelx)
y = cv2.filter2D(grayImage, cv2.CV_16S, kernely)
# 转uint8
absX = cv2.convertScaleAbs(x)
absY = cv2.convertScaleAbs(y)
Prewitt = cv2.addWeighted(absX, 0.5, absY, 0.5, 0)

# 用来正常显示中文标签
plt.rcParams['font.sans-serif'] = ['SimHei']

# 显示图形
plt.subplot(121),plt.imshow(img_RGB),plt.title('原始图像'), plt.axis('off') #坐标轴关闭
plt.subplot(122),plt.imshow(Prewitt, cmap=plt.cm.gray ),plt.title('Prewitt算子'), plt.axis('off')
plt.show()

常用图像卷积核类型小结

Sobel算子

Sobel算子则是Prewitt算子的改进版，对中间的元素适当进行了加权，Sobel算子与Prewitt算子类似。Sobel算子包含两组3×3的滤波器，分别对水平及垂直方向上的边缘敏感。

常用图像卷积核类型小结

让两个方向模板分别沿着x轴、y轴与图像做卷积，方向是从上到下和从左到右。将模板的中心和图像上的某个像素重合，并将该像素周围的点与模板上对应的系数相乘，如图所示，其中Gx及Gy分别代表经横向及纵向边缘检测的图像梯度值。

常用图像卷积核类型小结

图像上每个像素点的横向及纵向梯度值通过如下式结合，来计算该点梯度值G的大小：

常用图像卷积核类型小结

为了减少运算时间，提高运算效率，可以使用绝对值求和近似的方法代替开平方：

常用图像卷积核类型小结

由于Sobel算子对于象素的位置的影响做了加权，可以降低边缘模糊程度，与Prewitt算子、Roberts算子相比效果更好

from skimage import data,filters,img_as_ubyte
import matplotlib.pyplot as plt
import cv2

# 图像读取
img = data.camera()
plt.imshow(img,plt.cm.gray)

'''**********skimage*************'''
# sobel边缘检测
edges = filters.sobel(img)
# 浮点型转成uint8型
edges = img_as_ubyte(edges)
# 显示图像
plt.figure()
plt.imshow(edges,plt.cm.gray) 

# sobel 水平方向边缘检测
edgesh = filters.sobel_h(img)
edgesh = img_as_ubyte(edgesh)
plt.figure()
plt.imshow(edgesh,plt.cm.gray)

# sobel 竖直方向边缘检测
edgesv = filters.sobel_v(img)
edgesv = img_as_ubyte(edgesv)
plt.figure()
plt.imshow(edgesv,plt.cm.gray) 

'''**********opencv*************'''
# sobel边缘检测
edges = cv2.Sobel(img,cv2.CV_16S,1,1) 
# 浮点型转成uint8型
edges = cv2.convertScaleAbs(edges) 
plt.figure()
plt.imshow(edges,plt.cm.gray) 

# sobel 水平方向边缘检测
edges = cv2.Sobel(img,cv2.CV_16S,1,0) 
edgesh = cv2.convertScaleAbs(edgesh) 
plt.figure()
plt.imshow(edgesh,plt.cm.gray) 

# sobel 竖直方向边缘检测
edges = cv2.Sobel(img,cv2.CV_16S,0,1) 
edgesv = cv2.convertScaleAbs(edgesv) 
plt.figure()
plt.imshow(edgesv,plt.cm.gray)

分别是原图全方向solab算子

常用图像卷积核类型小结

竖直方向sobel检测水平向sobel检测

二阶微分算子

简介
上一小节介绍的Prewitt算子和Sobel算子都是近似对图像进行一阶导数的计算，只能提取出某个具体方向的边缘。由微积分的知识可知，一个函数的二阶导数为0时，代表此处的一阶导数取得极值，对应地也就表明原函数在此处的变化最大。比如著名的Sigmoid函数及其一阶导数、二阶导数的图像如下：

因此往往还可以根据图像的二阶导数过零点的位置，来预测图像中变化最剧烈的地方，也许对应物体的边缘。与一阶微分算子不同，这些二阶微分算子对边缘的计算具有旋转不变性，也就是可以检测出各个方向上的边缘。

Laplace算子

Laplace算子可以近似计算出图像的二阶导数，具有旋转不变性，也就是可以检测出各个方向的边缘。

常用图像卷积核类型小结

对于数字图像，拉普拉斯算子可以简化为：常用图像卷积核类型小结

也可以按卷积形式表示：
常用图像卷积核类型小结
其中K=1，I=1时H（r,s）取下式，四方面模板：

通过模板可以发现，当邻域内像素灰度相同时，模板的卷积运算结果为0；

当中心像素灰度高于邻域内其他像素的平均灰度时，模板的卷积运算结果为正数；

当中心像素的灰度低于邻域内其他像素的平均灰度时，模板的卷积的负数。

对卷积运算的结果用适当的衰弱因子处理并加在原中心像素上，就可以实现图像的锐化处理。

#coding=utf-8    
import cv2    
import numpy as np      
    
img = cv2.imread("test.jpg", 0)    
gray_lap = cv2.Laplacian(img,cv2.CV_16S,ksize = 3)    
dst = cv2.convertScaleAbs(gray_lap)    
    
cv2.imshow('laplacian',dst)    
cv2.waitKey(0)    
cv2.destroyAllWindows()

常用图像卷积核类型小结

对比:

锐化卷积核计算的是中心像素减去周围像素的差值（中心权重为正，周边权重为负）；而Laplace算子则是周围像素之和减去中心像素的差值（中心权重为负，周边权重为正）。

LoG算子

Laplace算子对噪声依然很敏感。因此常常先使用高斯滤波器对图像进行平滑操作，再使用Laplace算子计算二阶微分。二者结合称为LoG算子（Laplacian of Gaussian），该算子可以更加稳定地计算图像的二阶微分。

基本理论

高斯卷积函数定义为：

常用图像卷积核类型小结

而原始图像与高斯卷积定义为：

常用图像卷积核类型小结

因为：

常用图像卷积核类型小结

所以Laplacian of Gaussian(LOG) 常用图像卷积核类型小结可以通过先对高斯函数进行偏导操作，然后进行卷积求解。公式表示为：

常用图像卷积核类型小结

和

常用图像卷积核类型小结

因此，我们可以LOG核函数定义为：

常用图像卷积核类型小结

import numpy as np
import  cv2
from matplotlib import pyplot as plt

#定义掩膜
m1 = np.array([[0,0,-1,0,0],[0,-1,-2,-1,0],[-1,-2,16,-2,-1],[0,-1,-2,-1,0],[0,0,-1,0,0]]) #LoG算子模板

img = cv2.imread("lena_1.tiff",0)

#边缘扩充

image = cv2.copyMakeBorder(img, 2, 2, 2, 2, borderType=cv2.BORDER_REPLICATE)
# image = cv2.GaussianBlur(img,(3,3),4)
rows = image.shape[0]
cols = image.shape[1]
temp = 0
image1 = np.zeros(image.shape)

for i in range(2,rows-2):
    for j in range(2,cols-2):
        temp = np.abs(
            (np.dot(np.array([1, 1, 1, 1, 1]), (m1 * image[i - 2:i + 3, j - 2:j + 3])))
                .dot(np.array([[1], [1], [1], [1], [1]])))

        image1[i,j] = int(temp)

        if image1[i, j] > 255:
            image1[i, j] = 255
        else:
            image1[i, j] = 0


cv2.imshow("LoG",image1)

cv2.waitKey(0)

DoG算子

LoG算子的计算量较大，因此有数学家发明了DoG（Difference of Gaussians）算子来近似LoG算子。DoG算子翻译为高斯差分算子，从名称上可以看出，就是使用两个标准差不同的高斯滤波器对图像进行滤波操作，再将滤波后的两个结果相减，最后的结果可以近似LoG算子。其中涉及到的数学理论较为复杂，在此暂不讨论。

是灰度图像增强和角点检测(也叫特征点提取)的一种方法

基本理论

首先，高斯函数表示定义为：

常用图像卷积核类型小结

其次，两幅图像的高斯滤波表示为：

常用图像卷积核类型小结

最后，将上面滤波得到的两幅图像g1和g2相减得到：

常用图像卷积核类型小结

即：可以DOG表示为：

常用图像卷积核类型小结

高斯模糊代码

import cv2
import numpy as np
img = cv2.imread('D://fangzi.jpg')
cv2.imshow('img',img)
cv2.resizeWindow('img',640,480)
#img_ = cv2.GaussianBlur(img,ksize=(9,9),sigmaX=0,sigmaY=0)
img_ = cv2.GaussianBlur(img,(9,9),2)
cv2.imshow('img_',img_)
cv2.resizeWindow('img_',640,480)
cv2.waitKey()

效果：

常用图像卷积核类型小结

DOG代码

常用图像卷积核类型小结

左边是原图和三种不同σ的高斯模糊后的图。右边是对高斯滤波后的图片（相邻状态下）依次进行两两相减可得到右边的三个高斯函数的差分图（简称DOG）。

红色标记为当前像素点，黄色对应的像素点表示当前像素点邻接的点，共26(上图中27个黄点减去一个红点)个，如果该点（红点）是所有邻接像素点(黄点)的最大值或最小值，则红色标记对应的点为特征点。

#include <opencv2/opencv.hpp>
#include <iostream>

using namespace std;
using namespace cv;

int main()
{
    Mat ori_img = imread("D://lena.png");
    Mat gray_img;
    cvtColor(ori_img, gray_img, CV_RGB2GRAY);
    imshow("gray", gray_img);
    gray_img.convertTo(gray_img, CV_32F);// float -像素是在0-1.0之间的任意值，这对于一些数据集的计算很有用，但是它必须通过将每个像素乘以255来转换成8位来保存或显示。

    Mat gauss1, gauss2;
    GaussianBlur(gray_img, gauss1, Size(5, 5), 0.3, 0.3);
    GaussianBlur(gray_img, gauss2, Size(5, 5), 0.4, 0.4);

    Mat DoG1, DoG2, DoG3;
    DoG1 = gauss1 - gauss2;
    imshow("DOG1", DoG1);
    GaussianBlur(gray_img, gauss1, Size(5, 5), 0.6, 0.6);
    GaussianBlur(gray_img, gauss2, Size(5, 5), 0.7, 0.7);
    DoG2 = gauss1 - gauss2;
    imshow("DOG2", DoG2);
    GaussianBlur(gray_img, gauss1, Size(5, 5), 0.7, 0.7);
    GaussianBlur(gray_img, gauss2, Size(5, 5), 0.8, 0.8);
    DoG3 = gauss1 - gauss2;
    imshow("DOG3", DoG3);
    for (int j = 1; j < gray_img.rows - 1; j++)
    {
        for (int i = 1; i < gray_img.cols - 1; i++)
        {
            if (DoG2.at<float>(j, i) < DoG2.at<float>(j - 1, i - 1) && DoG2.at<float>(j, i) < DoG2.at<float>(j - 1, i) &&
                DoG2.at<float>(j, i) < DoG2.at<float>(j - 1, i + 1) && DoG2.at<float>(j, i) < DoG2.at<float>(j, i - 1) && DoG2.at<float>(j, i) < DoG2.at<float>(j, i + 1) &&
                DoG2.at<float>(j, i) < DoG2.at<float>(j + 1, i - 1) && DoG2.at<float>(j, i) < DoG2.at<float>(j + 1, i) && DoG2.at<float>(j, i) < DoG2.at<float>(j + 1, i + 1)
                && DoG2.at<float>(j, i) < DoG1.at<float>(j, i) && DoG2.at<float>(j, i) < DoG1.at<float>(j - 1, i - 1) && DoG2.at<float>(j, i) < DoG1.at<float>(j - 1, i) &&
                DoG2.at<float>(j, i) < DoG1.at<float>(j - 1, i + 1) && DoG2.at<float>(j, i) < DoG1.at<float>(j, i - 1) && DoG2.at<float>(j, i) < DoG1.at<float>(j, i + 1) &&
                DoG2.at<float>(j, i) < DoG1.at<float>(j + 1, i - 1) && DoG2.at<float>(j, i) < DoG1.at<float>(j + 1, i) && DoG2.at<float>(j, i) < DoG1.at<float>(j + 1, i + 1)
                && DoG2.at<float>(j, i) < DoG3.at<float>(j, i) && DoG2.at<float>(j, i) < DoG3.at<float>(j - 1, i - 1) && DoG2.at<float>(j, i) < DoG3.at<float>(j - 1, i) &&
                DoG2.at<float>(j, i) < DoG3.at<float>(j - 1, i + 1) && DoG2.at<float>(j, i) < DoG3.at<float>(j, i - 1) && DoG2.at<float>(j, i) < DoG3.at<float>(j, i + 1) &&
                DoG2.at<float>(j, i) < DoG3.at<float>(j + 1, i - 1) && DoG2.at<float>(j, i) < DoG3.at<float>(j + 1, i) && DoG2.at<float>(j, i) < DoG3.at<float>(j + 1, i + 1))
            {
                //cout << DoG2.at<float>(j, i);
                if (DoG2.at<float>(j, i) < -3)
                {
                    circle(ori_img, Point(i, j), 3, CV_RGB(0, 0, 255));
                }
            }
            else
                if (DoG2.at<float>(j, i) > DoG2.at<float>(j - 1, i - 1) && DoG2.at<float>(j, i) > DoG2.at<float>(j - 1, i) &&
                    DoG2.at<float>(j, i) > DoG2.at<float>(j - 1, i + 1) && DoG2.at<float>(j, i) > DoG2.at<float>(j, i - 1) && DoG2.at<float>(j, i) > DoG2.at<float>(j, i + 1) &&
                    DoG2.at<float>(j, i) > DoG2.at<float>(j + 1, i - 1) && DoG2.at<float>(j, i) > DoG2.at<float>(j + 1, i) && DoG2.at<float>(j, i) > DoG2.at<float>(j + 1, i + 1)
                    && DoG2.at<float>(j, i) > DoG1.at<float>(j, i) && DoG2.at<float>(j, i) > DoG1.at<float>(j - 1, i - 1) && DoG2.at<float>(j, i) > DoG1.at<float>(j - 1, i) &&
                    DoG2.at<float>(j, i) > DoG1.at<float>(j - 1, i + 1) && DoG2.at<float>(j, i) > DoG1.at<float>(j, i - 1) && DoG2.at<float>(j, i) > DoG1.at<float>(j, i + 1) &&
                    DoG2.at<float>(j, i) > DoG1.at<float>(j + 1, i - 1) && DoG2.at<float>(j, i) > DoG1.at<float>(j + 1, i) && DoG2.at<float>(j, i) > DoG1.at<float>(j + 1, i + 1)
                    && DoG2.at<float>(j, i) > DoG3.at<float>(j, i) && DoG2.at<float>(j, i) > DoG3.at<float>(j - 1, i - 1) && DoG2.at<float>(j, i) > DoG3.at<float>(j - 1, i) &&
                    DoG2.at<float>(j, i) > DoG3.at<float>(j - 1, i + 1) && DoG2.at<float>(j, i) > DoG3.at<float>(j, i - 1) && DoG2.at<float>(j, i) > DoG3.at<float>(j, i + 1) &&
                    DoG2.at<float>(j, i) > DoG3.at<float>(j + 1, i - 1) && DoG2.at<float>(j, i) > DoG3.at<float>(j + 1, i) && DoG2.at<float>(j, i) > DoG3.at<float>(j + 1, i + 1))
                {
                    if (DoG2.at<float>(j, i) > 3)
                    {
                        circle(ori_img, Point(i, j), 3, CV_RGB(255, 0, 0));
                    }
                }
        }
    }
    imshow("result", ori_img);
    waitKey(0);

效果：

输入的灰度图：常用图像卷积核类型小结