这个归并排序详解过程我能吹一辈子！！！-Toy模板网

这篇具有很好参考价值的文章主要介绍了这个归并排序详解过程我能吹一辈子！！！。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

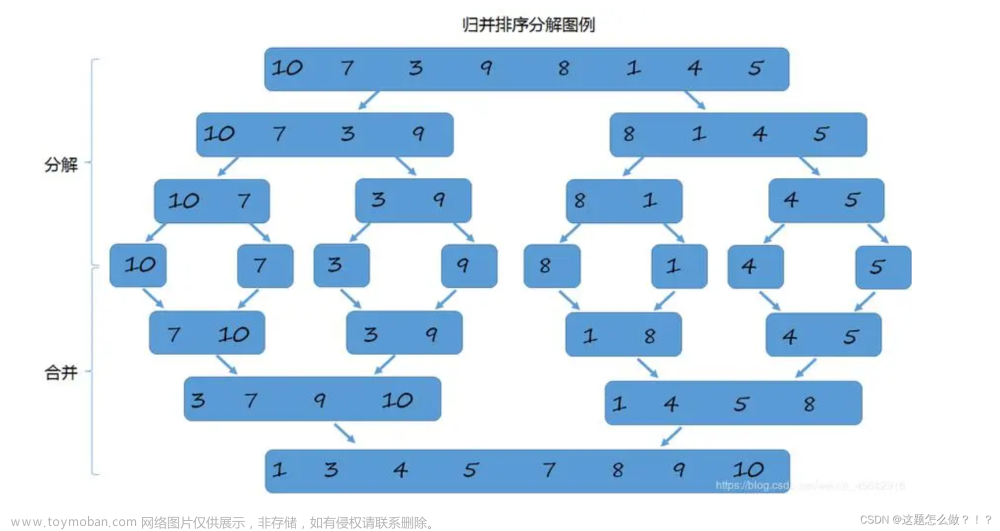
归并排序概念

1945年，约翰·冯·诺依曼（John von Neumann）发明了归并排序，这是典型的分治算法的应用。

归并排序（Merge sort）是建立在归并操作上的一种有效的排序算法，该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。

归并排序算法思路

归并排序算法有两个基本的操作，一个是分，也就是把原数组划分成两个子数组的过程。另一个是治，它将两个有序数组合并成一个更大的有序数组。

1> 将待排序的线性表不断地切分成若干个子表，直到每个子表只包含一个元素，这时，可以认为只包含一个元素的子表是有序表。
2> 将子表两两合并，每合并一次，就会产生一个新的且更长的有序表，重复这一步骤，直到最后只剩下一个子表，这个子表就是排好序的线性表。
这个归并排序详解过程我能吹一辈子！！！

相信大家都知道如何将两个有序序列合为一个有序序列吧：
这个归并排序详解过程我能吹一辈子！！！

那么如何得到有序的子序列呢？当序列分解到只有一个元素或是没有元素时，就可以认为是有序了，这时分解就结束了，开始合并：
这个归并排序详解过程我能吹一辈子！！！

归并排序递归实现

归并排序，从其思想上看就很适合使用递归来实现，并且用递归实现也比较简单。其间我们需要申请一个与待排序列大小相同的数组用于合并过程两个有序的子序列，合并完毕后再将数据拷贝回原数组。

代码示例：

//归并排序（子函数）
void _MergeSort(int* a, int left, int right, int* tmp)
{
	if (left >= right)//归并结束条件：当只有一个数据或是序列不存在时，不需要再分解
	{
		return;
	}
	int mid = left + (right - left) / 2;//中间下标
	_MergeSort(a, left, mid, tmp);//对左序列进行归并
	_MergeSort(a, mid + 1, right, tmp);//对右序列进行归并
	int begin1 = left, end1 = mid;
	int begin2 = mid + 1, end2 = right;
	//将两段子区间进行归并，归并结果放在tmp中
	int i = left;
	while (begin1 <= end1&&begin2 <= end2)
	{
		//将较小的数据优先放入tmp
		if (a[begin1] < a[begin2])
			tmp[i++] = a[begin1++];
		else
			tmp[i++] = a[begin2++];
	}
	//当遍历完其中一个区间，将另一个区间剩余的数据直接放到tmp的后面
	while (begin1 <= end1)
		tmp[i++] = a[begin1++];
	while (begin2 <= end2)
		tmp[i++] = a[begin2++];
	//归并完后，拷贝回原数组
	int j = 0;
	for (j = left; j <= right; j++)
		a[j] = tmp[j];
}
//归并排序（主体函数）
void MergeSort(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int)*n);//申请一个与原数组大小相同的空间
	if (tmp == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}
	_MergeSort(a, 0, n - 1, tmp);//归并排序
	free(tmp);//释放空间
}

时间复杂度：O(N*logN) 空间复杂度：O(N)

归并排序非递归实现

归并排序的非递归算法并不需要借助栈来完成，我们只需要控制每次参与合并的元素个数即可，最终便能使序列变为有序：
这个归并排序详解过程我能吹一辈子！！！
当然，以上例子是一个待排序列长度比较特殊的例子，我们若是想写出一个广泛适用的程序，必定需要考虑到某些极端情况：

情况一：
当最后一个小组进行合并时，第二个小区间存在，但是该区间元素个数不够gap个，这时我们需要在合并序列时，对第二个小区间的边界进行控制。
这个归并排序详解过程我能吹一辈子！！！

情况二：
当最后一个小组进行合并时，第二个小区间不存在，此时便不需要对该小组进行合并。
这个归并排序详解过程我能吹一辈子！！！

情况三：
当最后一个小组进行合并时，第二个小区间不存在，并且第一个小区间的元素个数不够gap个，此时也不需要对该小组进行合并。（可与情况二归为一类）
这个归并排序详解过程我能吹一辈子！！！

只要把控好这三种特殊情况，写出归并排序的非递归算法便轻而易举了。

代码示例：

//归并排序（子函数）
void _MergeSortNonR(int* a, int* tmp, int begin1, int end1, int begin2, int end2)
{
	int j = begin1;
	//将两段子区间进行归并，归并结果放在tmp中
	int i = begin1;
	while (begin1 <= end1&&begin2 <= end2)
	{
		//将较小的数据优先放入tmp
		if (a[begin1] < a[begin2])
			tmp[i++] = a[begin1++];
		else
			tmp[i++] = a[begin2++];
	}
	//当遍历完其中一个区间，将另一个区间剩余的数据直接放到tmp的后面
	while (begin1 <= end1)
		tmp[i++] = a[begin1++];
	while (begin2 <= end2)
		tmp[i++] = a[begin2++];
	//归并完后，拷贝回原数组
	for (; j <= end2; j++)
		a[j] = tmp[j];
}
//归并排序（主体函数）
void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int)*n);//申请一个与待排序列大小相同的空间，用于辅助合并序列
	if (tmp == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}
	int gap = 1;//需合并的子序列中元素的个数
	while (gap < n)
	{
		int i = 0;
		for (i = 0; i < n; i += 2 * gap)
		{
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;
			if (begin2 >= n)//最后一组的第二个小区间不存在或是第一个小区间不够gap个，此时不需要对该小组进行合并
				break;
			if (end2 >= n)//最后一组的第二个小区间不够gap个，则第二个小区间的后界变为数组的后界
				end2 = n - 1;
			_MergeSortNonR(a, tmp, begin1, end1, begin2, end2);//合并两个有序序列
		}
		gap = 2 * gap;//下一趟需合并的子序列中元素的个数翻倍
	}
	free(tmp);//释放空间
}