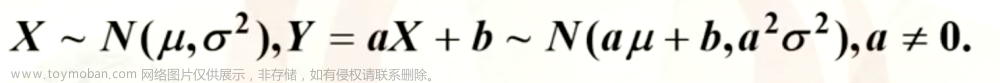一、正态分布(Normal distribution)的基本原理
正态分布(Normal distribution),也称“常态分布”,又名高斯分布(Gaussian distribution),最早由棣莫弗(Abraham de Moivre)在求二项分布的渐近公式中得到。C.F.高斯在研究测量误差时从另一个角度导出了它。P.S.拉普拉斯和高斯研究了它的性质。是一个在数学、物理及工程等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力。
若随机变量X服从一个数学期望为μ、方差为 σ 2 \sigma^2 σ2的正态分布,记为N(μ, σ 2 \sigma^2 σ2)。其概率密度函数为正态分布的期望值μ决定了其位置,其标准差σ决定了分布的幅度。当μ = 0,σ = 1时的正态分布是标准正态分布。
f ( x ∣ μ , σ ) = 1 2 π σ 2 e − ( x − μ ) 2 2 σ 2 f(x|\mu, \sigma) = \frac{1}{\sqrt{2\pi\sigma^{2}}}e^{-\frac{(x-\mu)^{2}}{2\sigma^{2}}} f(x∣μ,σ)=2πσ21e−2σ2(x−μ)2
其 μ \mu μ 是均值 、 σ \sigma σ 是标准差

- 与x轴不相交
- 单峰(最大值为x=u)
- 最大值: 1 σ 2 π \frac{1}{\sigma\sqrt{2\pi}} σ2π1
- 曲线与x轴之间的面积S=1
二、正态分布检验(Test of Normality)
正态分布在统计学中有着极为重要的地位,常见的t检验、方差分析、person相关等统计方法的前提都要求数据服从正态分布。

2.1、正态分布直方图、核密度图、P-P图、Q-Q图
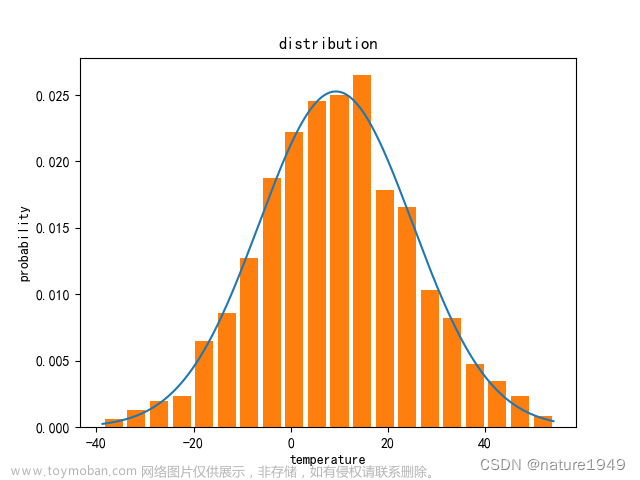
- 正态性检验直方图
若正态图基本上呈现出钟形(中间高,两端低),则说明数据虽然不是绝对正态,但基本可接受为正态分布。

-
核密度图
-
分位数图(Quantile-quantile Plot,Q-Q图)
分位图(Q–Q plot)又称QQ 图,Q 代表分位数(Quantile)Q-Q图,全称“Quantile Quantile Plot”,用图形的方式比较观测值与预测值(假定正态下的分布)不同分位数的概率分布,从而检验是否吻合正态分布规律。并且将实际数据作为X轴,将假定正态时的数据分位数作为Y轴,作散点图,散点与直线重合度越高越服从正态分布,散点差异愈大越不服从正态分布,请视实际情况而定。

- 概率图(Probability-probability Plot,P-P图)
P-P 图是根据变量的累积比例与指定分布的累积比例之间的关系所绘制的图形。通过 P-P 图可以检验数据是否符合指定的分布。当数据符合指定分布时,P-P 图中各点近似呈一条直线。 如果在绘制中 P-P 图中各点不呈直线,但有一定规律,可以对变量数据进行转换,使转换后的数据更接近指定分布。

2.2、偏度-峰度检验法、JB(Jarque Bera)检验
- 偏度(skewness)也称偏态、偏态系数:主要用于判定数据的对称性,整体数据偏左还是偏右;
- 峰度(kurtosis):用于判定数据分布的陡缓程度;
正态分布的偏度为0和峰度为 3,其中偏度和峰度的定义分别为
b
s
=
E
[
(
X
−
u
σ
)
3
]
b_s = E[(\frac{X-u}{\sigma})^3]
bs=E[(σX−u)3]
k
=
E
[
(
X
−
u
σ
)
4
]
k = E[(\frac{X-u}{\sigma})^4]
k=E[(σX−u)4]
正态性检验要求严格很难满足,如果峰度绝对值小于10并且偏度绝对值小于3,则说明数据虽然不是绝对正态,但基本可接受为正态分布;
- JB(Jarque Bera)检验
JB统计量:
J
B
=
n
6
[
b
s
2
+
(
k
−
3
)
4
4
]
JB = \frac{n}{6}[b_s^2+\frac{(k-3)^4}{4}]
JB=6n[bs2+4(k−3)4]
证明在正态性假定下
J
B
∼
x
2
(
2
)
JB \sim x^2(2)
JB∼x2(2),如果变量服从正态分布,则
b
s
b_s
bs为零,k为3,因而JB统计量的值为零。如果不是正态分布,则JB统计量将是一个逐渐增大的值。
2.3、Shapiro-Wilk检验(3 ≤ \le ≤ n < 5000)
SW检验用于验证一个随机样本数据是否来自正态分布,从统计学意义上将样本分布与正态分布进行比较,以便确定数据是否显示出正态性的偏移或符合。
- step1:假设待检验数据为: x ( 1 ) < x ( 2 ) < . . . < x ( n ) x_{(1)} < x_{(2)} < ... <x_{(n)} x(1)<x(2)<...<x(n)
- step2:建立零假设:样本所来自的总体分布服从正态分布
- step3:构建统计量:
W = ( ∑ i = 1 n a i x ( i ) ) 2 ∑ i = 1 2 ( x ( i ) − x ˉ ) 2 W = \frac{(\sum_{i=1}^na_ix_{(i)})^2}{\sum_{i=1}^2(x_{(i)} - \bar x )^2} W=∑i=12(x(i)−xˉ)2(∑i=1naix(i))2
其中 x ˉ \bar x xˉ是样本的平均值;常量 ( a 1 , . . . , a n ) = m T V − 1 ( m T V − 1 V − 1 m ) 1 / 2 (a_1,...,a_n)=\frac{m^TV^{-1}}{(m^TV^{-1}V^{-1}m)^{1/2}} (a1,...,an)=(mTV−1V−1m)1/2mTV−1,其中 m = ( m 1 , . . . , m n ) T m=(m_1,...,m_n)^T m=(m1,...,mn)T是从一个标准的正态分布随机变量上采样的有序独立同分布的统计量的期望值。V是这些有序统计量的协方差。
-
step4:计算检验统计量W,其与判断临界值 W α W_{\alpha} Wα比较
-
step5:判断统计值是否呈现出显著性(p值小于0.05或0.01),如果呈现出显著性,则说明该项不具有正态分布特质,如果需要对比不同组别数据差异性,可考虑使用非参数检验;如果没有呈现出显著性(P>0.05),说明该项具有正态分布特质。文章来源:https://www.toymoban.com/news/detail-454071.html
from scipy import stats
stats.shapiro(x)
2.4、Kolmogorov–Smirnov检验(n≥50)
Kolmogorov-Smirnov检验(简称K-S检验)是检验单一样本是否来自某一特定分布,或者说检验两个经验分布是否不同或一个经验分布与另一个理想分布是否不同。其检验方法通常是是以样本数据的累积频数分布与特定理论分布比较,若两者间的差距很小,则推论该样本取自某特定分布。它是一种基于ECDF(经验累积分布函数,是样本累积分布函数对实际累积分布函数的近似)检验,由于K-S检验构建的是一个D统计量,因此也称为D检验,同样被称为D检验的还有一个D‘Agostino‘s K-squared正态性检验,K-S检验只适用于连续和定量数据,并且样本量至少要50以上文章来源地址https://www.toymoban.com/news/detail-454071.html
到了这里,关于统计基础:1.1_正态分布及其检验的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!