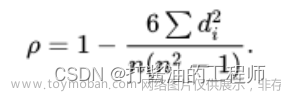spss统计分析书中这样写到:
在线性回归模型中,有一个同方差性假设,就是要求所有观测对回归模型的变异具有相同的贡献,以此为基础的回归方法称之为普通最小二乘法(OLS)。当因某些观测的变异较其他观测大而导致样本的方差不等时,就不能使用OLS方法了。如果观测的变异是可以通过其他变量进行预测,就可以使用加权最小二乘法(WLS)来拟合线性回归模型。WLS实际上是在回归中按观测量方差的倒数对观测进行加权,这样就会降低具有较大方差的观测记录对计算过程的影响。
例如在研究通货膨胀和失业率对股票价格的影响时,考虑到高市值的股票较低市值的具有更高的变异性(价格波动大),使用OLS法便不能很好地反应制定因素对变异性较大的股票的影响,这个时候就需要使用WLS方法来解决这个问题
数学公式:
它的回归方程仍然是
唯一区别是代价函数变成了 w为权重
w为权重
数据要求和假设:
-
自变量和因变量:应该是数值型变量,类似于宗教、民族和地区这样的分类变量应该重新编码成二分类变量或其他的对照(contrast)变量;
-
加权变量必须是与因变量有关的数值型变量;
-
对于自变量的每个取值,对应因变量的取值分布必须是正态的;
-
因变量和每一个自变量的相关关系应该是线性的;
-
所有观测量之间相互独立;
-
各观测的方差可以不同,但是这些差异可以通过加权变量进行预测;
spss中的回归有很多,单因素、多因素线性回归,曲线回归,逻辑斯蒂回归(分类问题)等等。
spss中至少有两种方式实现加权线性回归:
一种是在线性回归中直接指定WLS权重
这种指定的可以新建一列数据,如果是实验的频次不同则可以通过频次的数量来加权,实验次数多的权重大。或者还有其他指定权重的方式。
另一种就是回归中的权重估算
这种指定的权重变量只需要设定权重变量和幂范围就可以了,软件会自动计算幂范围内的每一个权重,权重为权重变量取幂后的倒数 公式:1/(weight variable)**n,步长为设定的0.5或其他,进而得到对数似然值最大的那个n,并计算得到最佳权重,用最佳的权重进行加权回归。
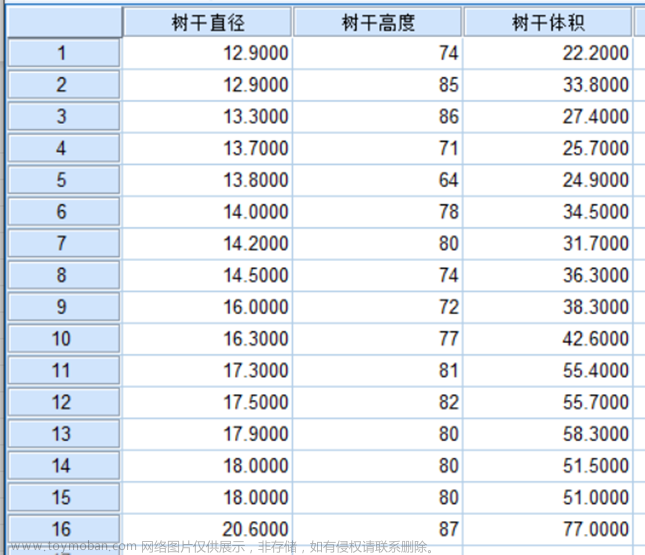
还是以spss自带的数据 “mallcost.sav“ 进行分析。
使用加权最小二乘法,主要过程分为方差诊断和权重估计两个步骤
方差诊断:
先利用OLS方法对原始数据建立简单线性模型,并绘制其残差对预测值的散点图,如果残差均匀分布在某条与横轴平行的横线附近说明样本的方差基本相等;反之,如果方差呈现明显的喇叭口形状或其他不规则形状,说明样本方差不相等,有必要进行WLS估计。
如果只有一个自变量,可以直接作因变量对自变量的散点图,观察因变量的分布是否均匀,判断方法与残差图相似。
估计权重
如果认为因变量的方差与其他变量之间存在着相关关系,就可以使用WLS来估计权重,常用的估计方法有如下两种:
①利用数据的复制集来估计权重。
要使用WLS估计回归模型,就需要先计算每一个观测的变异性。一种比较好的方法是将具有相同特点或近似特点的数据进行编组(数据的复制集),然后计算因变量在各编组中的方差,并以此方差的倒数作为相应编组中观测的权重。
②利用变量估计权重。
利用方差与其他变量的相关关系估计权重,因变量的方差经常与自变量有关。例如:高市值的股票价格具有较大的方差,具有研究生学历的人员的工资方差要比那些没有获得学位人员的工资方差高出许多。
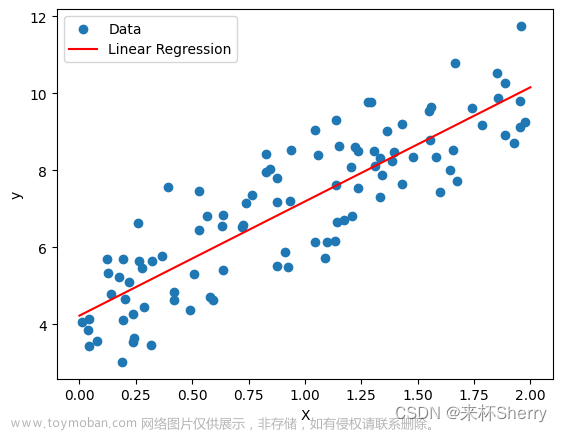
先用线性回归看一下残差的分布情况图为:
上图中随着预测值的增大,残差也有增大的趋势,故而可以否定OLS中关于同方差的假设,建议采用WLS方法对这个问题进行分析。
用权重估计进行回归:
最终得到的结果

对数似然值中3.5取值出对数似然值最大。所以加权中的幂取3.5.
R方也大
从F统计量的显著性看远小于0.05,因此由加权回归模型所解释的变异系数远大于由残差所解释的变异系数,回归效果很好
由系数估计结果可看出,各个变量系数及常数项的t检验的Sig的值均小于显著性水平0.05,因此加权回归模型的系数显著有效
最终的公式为:53.438+149.273×面积-26.533×商业街种类-2.209×从业年数
并且最终在原表中增加了一列为权重值,为:面积**(-3.5)
如果此时选择第一种用线性回归模型,选择WLS权重栏中点入这个数据,那么和加权分析得到的系数结果都是一样的。
我们用公式计算出他的预测值,然后用 sum(权重*(y真实值-y预测值)**2)得到的残差结果就是上表中的78612.250
我感觉这个例子不是很好,因为我计算出来残差以后,绘出残差的分布图,感觉也不是很好。随着预测值的增加残差也会增大,只是异常单变少了。还在研究中。但是比其他的回归方式好很多,我试了各种的回归,残差都很大,只有这一个是最小的。
以上所有,都是书中或者网络上已经说得很清楚了,但是还是有很多疑点,比如数据量很多,在使用线性回归后效果不显著,残差分布不理想的,改用加权回归后,应该对哪一个数据进行加权,要怎么选择,只是说与因变量有关的数值型变量,如果有两个参数同时对因变量印象很大呢,很多都没有给出具体的说明。
就像本例中为什么选择面积,也没有说明。
那么想一下,权重估计是在残差平方乘上权重,再求和,如果这一行数据会使得残差波动变大,那么这一行的权重就应该相应的降低,这样才能保证最终残差的稳定。
那么在这一行也就一定有影响y_pred的值波动很大的变量。
对于同样上面的数据,我们在进行一次线性回归,然后保存标准化后的残差值。
这是不加权重估计的,得到的残差一定是不齐性的,上面已经说过了。
那么这个残差和不同变量之间的关系又是怎样的?
我们绘制散点图,用标准化残差做y轴,分别用面积和建筑师从业年数做x轴。看一下随着面积或者从业年数的增加,标准化残差的变化。
分别得到下面的图:

对于上面两张图,很明显的能看到他们的位置信息变化规律。当面积增大时,残差也会相应的增大,当从业年数增大时,残差没有明显的变化规律。所以面积对残差的影响大于从业年数。
可以看出面积在增大,残差在增大,所以面积越大,它所拥有的权重就应该越小。由于权重是变量导数的n次幂,针对面积越大权重应该越小的法则,这个n应该为正数,所以本例在书本中也是直接填写的正数1-5。网上也有负数的案例。文章来源:https://www.toymoban.com/news/detail-454308.html
总结:对于加权回归,其实还是在线性回归的基础上,只是更改了损失函数,加了权重,这个权重的意义就是这一行数据某一个变量对结果的影响的重要性,接下来就是怎么找,找到后怎么做,结果的理想程度能不能接受。文章来源地址https://www.toymoban.com/news/detail-454308.html
到了这里,关于SPSS----加权回归分析你了解多少(随笔笔记)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!