FPGA实现对锯齿波的FFT分析-Toy模板网

这篇具有很好参考价值的文章主要介绍了FPGA实现对锯齿波的FFT分析。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

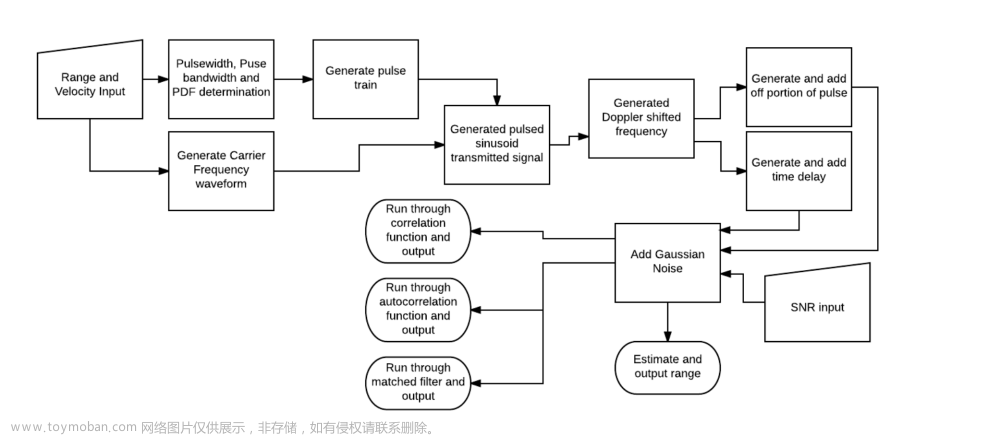
1.傅里叶级数展开

由信号与系统知识：

任意一个周期函数的傅里叶级数构造出来的三角函数展开式形式为：

FPGA实现对锯齿波的FFT分析

其中2pi/T是原始信号的角频率，因为n>1，可见分量的角频率必然不小于原始信号的频率，是原始信号频率的整数倍。所以这里的n不是索引序号，而是分量的角频率与原始信号角频率的倍数关系，如果没有某个倍数对应的分量，那么这一项就是0。

FPGA实现对锯齿波的FFT分析

锯齿波的傅里叶级数可展开为如下形式：

FPGA实现对锯齿波的FFT分析

锯齿波傅里叶级数展开例子

2.DFT与FFT

信号处理算法用以准确分析取样信号的幅值和相位差，为计算阻抗和功率提供依据。对于基波和谐波信号的分析，在数字信号处理领域通常使用快速傅里叶变换（FFT）用于频谱分析，提取基波和各次谐波的频率、幅值及相位差。

DFT运算公式为：

FPGA实现对锯齿波的FFT分析

此处不复述DFT与FFT原理，直接写出FFT结果，对于一个点数为N的离散信号序列，经过 FFT 处理后得到的是N点的复数结果为：

FPGA实现对锯齿波的FFT分析

其中k是N点的复数结果中的第k个值的序号，对应频谱中的第k条谱线， FPGA实现对锯齿波的FFT分析分别表示复数结果中X(k)的实部和虚部。根据X(k)可以计算得到每条谱线的幅值A(k)和相位θ(k)：

FPGA实现对锯齿波的FFT分析

设采用频率为fs，则FFT频谱中第k条谱线对应的频率为：

FPGA实现对锯齿波的FFT分析

其中∆f 称为FFT的频率分辨率，它反映了FFT频谱中谱线之间的频率间隔。

此时根据FPGA的设置采样点数N与ADC采集频率，便可推算出对应频率的k值，从而得到需求频率处的幅值A(k)和相位θ(k)，用于后续的数据处理。

3.Matlab仿真实验

假设连续信号为5*sawtooth(w.*t+pi);w=2*pi

即被采样信号为锯齿波 FPGA实现对锯齿波的FFT分析的周期信号，周期为1Hz。

则其傅里叶级数展开可表示为：

FPGA实现对锯齿波的FFT分析

所以其基波幅值为10/π。

采用Matlab模拟FPGA实际采集情况：采样频率为50MHz，被采集信号为1MHz的锯齿波，（简化运算量，Matlab中设置为50Hz与1Hz，故角频率w=2πf=2π(rad/s)，采样点数为N=2048。采用离散傅里叶变换函数DFT/FFT对信号进行采集并绘制5*sawtooth(w.*t+pi)与2.5*sawtooth(w.*t+pi)振幅与相位特性：

FPGA实现对锯齿波的FFT分析

锯齿波FFT仿真结果

对5*sawtooth(w.*t+pi)的频谱分析，由前式知想获取基波幅值与相位信息，则距离基频1Hz最近的谱线为：

FPGA实现对锯齿波的FFT分析

可计算基波幅值相位：

FPGA实现对锯齿波的FFT分析

考虑采用比值校正法对频谱泄露问题进行改善，比值校正法的实质是在FFT计算得到的频谱的基础上，根据所选用的窗函数计算归一化的频率校正量∆k，并使用∆k对信号峰值谱线所对应的幅值、相位和频率进行补偿。

FPGA实现对锯齿波的FFT分析

得到校正后的基波的幅值相位频率：

FPGA实现对锯齿波的FFT分析

可见通过比值校正后其幅值相位频率均得到了有效的改善；与锯齿波傅里叶级数展开式比较，其基波幅值相等，符合理论计算。

4.FPGA调用IP核实现锯齿波FFT计算

硬件平台：博宸精芯ZYNQ_MINI，主控芯片为xc7z010clg400-1。（如果只是仿真方案合理性不需要硬件平台）。

首先为了保证Matlab中的锯齿波采样序列与FPGA送入FFT的采样序列保持完全一致，前规定好Matlab中采样序列为xn1=500*sawtooth(w.*t)+500; w=2*pi; 此处加了500的直流偏置，是为了在FPGA中简化程序。此时锯齿波采样序列如下图，其在0点采样值为0，49点采样值为980。（此处的图像展示省略了100~2047采样点）。

FPGA实现对锯齿波的FFT分析

500*sawtooth(w.*t)+500锯齿波采样序列

4.1 配置IP核

接下来在Vivado中调用并配置IP核：（可参考官方文档https://docs.xilinx.com/internal/api/webapp/print/a36e63a0-2c43-4d40-8f3d-2b84ea4974cb）

以及该文章Vivado IP核：FFT实验 - 知乎 (zhihu.com)

工程组成包括一个fft_top顶层文件，以及一个fft_tb仿真文件：

FPGA实现对锯齿波的FFT分析

IP核设置：

FPGA实现对锯齿波的FFT分析

4.2顶层代码编写

首先可以在IP Sources中找到xfft_0.veo中的端口例子，将其复制到自己的主程序：

FPGA实现对锯齿波的FFT分析

首先来看看fft模块的端口参数意义：

FPGA实现对锯齿波的FFT分析

（1）第一个部分是配置FFT的信息，我们通过控制这些输入信号，来控制FFT的运作方式。

.aclk(clk),//输入端口：输入时钟（根IP核设置保持一致）；

.s_axis_config_tdata(8'd1),//输入端口：配置数据，给1为FFT，0为IFFT；

.s_axis_config_tvalid(1'd1),//输入端口：1则开始进行FFT配置，0停止；

.s_axis_config_tready(),//输出端口：当FFT配置好时，会给标志。

（2）第二部分是FFT信号输入模块

.s_axis_data_tdata({20'd0,ad_ch1}), //输入端口：(输入数据，高n位为虚部，低n位为实部）

需要注意的是，高16位为虚部，低16为是实部。这里我的输入数据是12位的实数，需要令高20位为0，再把它们拼接起来；

.s_axis_data_tvalid(dat_valid),//输入端口：1则开始进行FFT计算，0停止；

.s_axis_data_tready(),//输出端口：准备好数据输入通道的输出标志；

.s_axis_data_tlast(dat_last),//输入端口：最后一个数据标志位，便于结束FFT。

（3）第三部分FFT计算后输出模块

.m_axis_data_tdata(fft_out),//输出端口：FFT的输出值高n位为虚部，低n位为实部

.m_axis_data_tuser(fft_user),//输出端口：FFT输出数据的地址

.m_axis_data_tvalid(out_valid),//输出端口：当FFT开始输出时，该标志位一直置1，计算结束后，该位置0（用该标志来将此次FFT运算结果存入RAM后续进行处理）

.m_axis_data_tready(1'd1),//输入端口：表示它能够提供示例数据。一直置1即可

.m_axis_data_tlast(),//输出端口：最后一个输出数据标志位可用于判断此次FFT运算是否已经结束（不用可不连）

（5）顶层代码fft_top.v

1.	module fft_top(  
2.	    input [11:0]ad_ch1,  
3.	    input clk,  
4.	    input dat_last,  
5.	    input dat_valid,  
6.	   
7.	    output out_valid,  
8.	    output [15:0]out_user,  
9.	    output [23:0]out_im,  
10.	    output [23:0]out_re  
11.	    );  
12.	      
13.	wire [47:0]fft_out;  
14.	wire [15:0]fft_user;  
15.	xfft_0 fft_test(  
16.	  
17.	      .aclk(clk),//输入端口：输入时钟（根IP核设置保持一致）  
18.	      .s_axis_config_tdata(8'd1),//输入端口：配置数据，给1为FFT，0为IFFT  
19.	      .s_axis_config_tvalid(1'd1),//输入端口：1则开始进行FFT配置，0停止  
20.	      .s_axis_config_tready(),//输出端口：当FFT配置好时，会给标志  
21.	        
22.	      .s_axis_data_tdata({20'd0,ad_ch1}), //输入端口：(输入数据，高n位为虚部，低n位为实部）  
23.	      .s_axis_data_tvalid(dat_valid),//输入端口：1则开始进行FFT计算，0停止  
24.	      .s_axis_data_tready(),//输出端口：准备好数据输入通道的输出标志  
25.	      .s_axis_data_tlast(dat_last),//输入端口：最后一个数据标志位，便于结束FFT  
26.	        
27.	      .m_axis_data_tdata(fft_out),//输出端口：FFT的输出值 高n位为虚部，低n位为实部  
28.	      .m_axis_data_tuser(fft_user),//输出端口：FFT输出数据的地址  
29.	      .m_axis_data_tvalid(out_valid),//输出端口：当FFT开始输出时，该标志位一直置1，计算结束后，该位置0（用该标志来将此次FFT运算结果存入RAM后续进行处理）  
30.	      .m_axis_data_tready(1'd1),//输入端口：表示它能够提供示例数据。一直置1即可  
31.	      .m_axis_data_tlast(),//输出端口：最后一个输出数据标志位 可用于判断此次FFT运算是否已经结束（不用可不连）  
32.	        
33.	      //事件端口 暂时不用可不连接  
34.	      .event_frame_started(),  
35.	      .event_tlast_unexpected(),  
36.	      .event_tlast_missing(),  
37.	      .event_status_channel_halt(),  
38.	      .event_data_in_channel_halt(),  
39.	      .event_data_out_channel_halt()  
40.	  
41.	);  
42.	    assign out_re = fft_out[23:0]; //FFT输出实部   
43.	    assign out_im = fft_out[47:24];//FFT输出虚部  
44.	    assign out_user=fft_user;//地址  
45.	      
46.	endmodule

4.3 仿真文件代码fft_tb.v(需在自己的路径下创建相应的txt文件，且路径改为自己电脑的。)

`timescale 1ns / 1ps
module fft_tb();

    reg [11:0]ad_ch1;
    reg clk;
    reg dat_last;
    reg dat_valid;
    wire [23:0]out_im;
    wire [23:0]out_re;
    wire [15:0]out_user;
    wire out_valid;

    
    reg [23:0]reg_out_im;
    reg [23:0]reg_out_re;
 
    integer i;//数据输入变量
    integer fid_out_re;//存放数据文件路径
    integer fid_out_im;//存放数据文件路径
 
    always #10 clk <= ~clk; //生成时钟50MHz

    fft_top fft_top_inst(//例化代码
    .ad_ch1(ad_ch1),
    .clk(clk),
    .dat_last(dat_last),
    .dat_valid(dat_valid),
    .out_valid(out_valid),
    .out_user(out_user),
    .out_im(out_im),
    .out_re(out_re)
    );
 ///
    initial begin
        clk        <= 1'd1;
        ad_ch1     <= 12'd0;
        dat_valid  <= 1'b0;
        dat_last   <= 1'b0;
              
        fid_out_re = $fopen("C:/Users/AHZ/Desktop/fft_test/data/out_re.txt","w"); 
        fid_out_im = $fopen("C:/Users/AHZ/Desktop/fft_test/data/out_im.txt","w");
        #10;
        for(i=0;i<=2047;i=i+1)begin
            dat_valid <= 1;//dat_valid置1 表示数据开始输入给FFT
            if(i!=0)begin
                ad_ch1 <=ad_ch1+20;//锯齿波的 第一个采样点是0  后续每次加20 模拟了1MHz锯齿波被50MHz的ADC采集 从0~1000的情况
                end
            if(ad_ch1==980)begin//如果采集到980 则代表一个周期采集完毕 ad_ch1置0 （xn1=500*sawtooth(w.*t)+500; w=2*pi*1MHz; ）
                ad_ch1<=0;
                end
            #20;//采样率50MHz 所以每两个采集点间隔位20ns
        end
        
        dat_last <= 1;//dat_last置1 表示数据输入结束
        ad_ch1 <= 12'd0;       
        #20000000;
    end
 
    always @ (posedge clk) begin    
          $fwrite(fid_out_re,"%d\n",$signed(reg_out_re[23:0])); //reg_out_re数据保存在txt文本中
          $fwrite(fid_out_im,"%d\n",$signed(reg_out_im[23:0])); //reg_out_im数据保存在txt文本中          
    end

 
     always @ (posedge clk) begin                //fft输出结果到寄存器中保存，使数据更稳定
               reg_out_im <= out_im;
               reg_out_re <= out_re;
    end
 
     always @ (posedge clk) begin               //如果输出标志位out_valid置0 则代表FFT数据输出结束 把reg_out_re reg_out_im置0
       if(!out_valid) begin    
                  reg_out_re <= 24'd0;
                  reg_out_im <= 24'd0;
       end
    end
endmodule

4.4实验结果

FPGA实现对锯齿波的FFT分析

（1）Dat_valid置1时，ad_ch1数据开始累加，并送入FFT；dat_last置1时数据输入完毕。

（2）数据输入结束后大约延迟250us后FFT的out_im和out_re开始输出。输出时out_valid置1。

（3）out_user代表输出的谱线序号，从0~2047累加为止，例如0谱线对应 FPGA实现对锯齿波的FFT分析。

后续在Matlab中进行数据处理：

将txt文件中out_im和out_re结果取出先放入excel进行转置操作，然后粘贴入Matlab的变量中：

FPGA实现对锯齿波的FFT分析

定义fpga_y=fpga_im+i*fpga_re，则此时fpga_y表示FPGA的FFT输出的2048个复数。比较Matlab与FPGA的FFT输出幅度曲线随序列点的关系，两者一致：

FPGA实现对锯齿波的FFT分析

同一锯齿波信号 Matlab与FPGA的FFT处理结果文章来源地址https://www.toymoban.com/news/detail-455003.html

Matlab仿真代码：

frequency=1;%基波频率
N=2048;%采样点数
fc=50; %采样频率
w=2*pi;%被采信号频率
n=[0:N-1];%采样序列
t=n/fc;%采样时间
k1=0;%离散频谱校正幅值1次大值序号
k1plus=0;%离散频谱校正幅值1最大值序号
k2=0;%离散频谱校正幅值2次大值序号
k2plus=0;%离散频谱校正幅值2最大值序号
xn1=500*sawtooth(w.*t)+500;%被采信号1序列
xn2=250*sawtooth(w.*t);%被采信号2序列

t=cputime;
y1=fft(xn1,N);%被采信号1序列FFT变换
y2=fft(xn2,N);%被采信号1序列FFT变换
Time_fft=cputime-t;
Mag1=2/N*abs(y1);%被采信号1幅值序列
Mag2=2/N*abs(y2);%被采信号2幅值序列
Mag_fpga=2/N*abs(fpga_y);%被采信号 FPGA测试 幅值序列 此处需要先从excel导入
[k1,k1plus]=ratio_correction(Mag1,frequency,fc,N);
[k2,k2plus]=ratio_correction(Mag2,frequency,fc,N);

Phase1=angle(y1);%被采信号1相位序列
Phase2=angle(y2);%被采信号1相位序列
f=n*fc/N;%各次谐波频率 
 

figure(1)%500*sawtooth(w.*t)+500与250*sawtooth(w.*t)FFT结果
subplot(3,2,1)
stem(n,xn1,'.K','LineWidth',2);axis([0,100,0,1000])
title('500*sawtooth(2pi*t)原信号序列')
xlabel('信号1序列点');
ylabel('幅值');grid on;

subplot(3,2,2)
stem(n,xn2,'.K','LineWidth',2);axis([0,100,-250,250])
title('250*sawtooth(2pi*t)原信号序列')
xlabel('信号2序列点');
ylabel('幅值');grid on;


subplot(3,2,3),plot(n,Mag1,'K','LineWidth',2);
title('信号1振幅与相位特性');
xlabel('信号1序列点');
ylabel('振幅');grid on;
 
subplot(3,2,4),plot(n,Mag2,'K','LineWidth',2);
title('信号2振幅与相位特性');
xlabel('信号2序列点');
ylabel('振幅');grid on;

subplot(3,2,5),plot(n,Phase1,'K','LineWidth',2);
xlabel('信号1序列点');
ylabel('相位');grid on;

subplot(3,2,6),plot(n,Phase2,'K','LineWidth',2);
xlabel('信号2序列点');
ylabel('相位');grid on;


figure(2)
stem(n,xn1,'.K','LineWidth',2);axis([0,2048,-500,500])
subplot(2,1,1),plot(n,Mag_fpga,'K','LineWidth',2);
title('FPGA振幅特性');
xlabel('信号1序列点');
ylabel('振幅');grid on;

subplot(2,1,2),plot(n,Mag1,'K','LineWidth',2);
title('Matlab FFT振幅特性');
xlabel('信号1序列点');
ylabel('振幅');grid on;




%%离散频谱校正-比值校正法
ratio1 = Mag1(k1)/Mag1(k1plus);
delta_k1=-1/(1+ratio1);
if(abs(delta_k1+1)>0.01)%如果采样谱线不在需求频率处（离散频谱校正）
    Amp1_Cor=pi*delta_k1*Mag1(k1)/sin(pi*delta_k1)
    frequency1=(k1-1-delta_k1)*fc/N
    Angle1=Phase1(k1plus)+pi*delta_k1;
else                    %如果采样谱线刚好在需求频率处
    Amp1_Cor=Mag1(k1plus)
    frequency1=frequency
    Angle1=Phase1(k1plus)
end

ratio2 = Mag2(k2)/Mag2(k2plus);
delta_k2=-1/(1+ratio2);
if(abs(delta_k2+1)>0.01)%如果采样谱线不在需求频率处（离散频谱校正）
    Amp2_Cor=pi*delta_k2*Mag2(k2)/sin(pi*delta_k2)
    frequency2=(k2-1-delta_k2)*fc/N
    Angle2=Phase2(k1plus)+pi*delta_k2;
else                    %如果采样谱线刚好在需求频率处
    Amp2_Cor=Mag2(k2plus)
    frequency2=frequency
    Angle2=Phase2(k2plus)
end

angle_dif=(Angle1-Angle2)/pi*180  %求相位差

到了这里，关于FPGA实现对锯齿波的FFT分析的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！