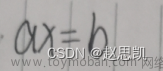置换矩阵就是重新排列后的单位矩阵
对一个矩阵进行行交换,需要通过置换矩阵(permutation matrix)来完成。
在对一个Ax=b的方程组进行高斯消元的过程中,我们常常会遇到一种情况,也就是消元消不下去的情况。下面,我列出了两个不同的3x3矩阵的消元过程:

上图中的第一行,是一个比较常见的消元流程。对于3x3方阵而言,先令主对角线上的第一个元素A11(在图中左上角用方框框出)为主元(pivot),且当前列被称为主元列。用A11所在的行去乘以一个合适的系数减去下面各行(第二,第三行),使得A11这一列下面的元素都为0。之后,再令A22为主元,A22所在的列为主元列,用A22所在的行乘以一个相应的系数减去下面各行(第三行),使得A22所在列下面的元素都为0。一直进行到,对角线上的最后一个元素。
但有时候,我们在消元过程中可能会遇到主对角线上为0的情况,正如上图中的第二个消元过程。当消元进行到主对角线上的A22(图中第二行第二步中用方框框出来的元素)时,消元无法进行下去了。因为,0无论乘以任何系数都无法消除0下面的元素。这时,我们就要把A22下面的非零元素所在的行,和A22所在的行,进行行交换。使得主对角线上的A22不为0,并完成后续的消元过程。
上面提到的行交换的矩阵表达形式就是置换矩阵P。也就是用置换矩阵P左乘以该矩阵。例如,我们下面这个例子:

消元一开始就遇到了问题,主对角线上的第一个元素A11=0,消元进行不下去了。这时我们只需把上面的两行对调一下就可以得到下面的方程组。

而如果我们把这一过程用矩阵的形式来表现的话就是:


重点:现在我再重申一遍这篇文章开头的标题,置换矩阵就是重新排列后的单位矩阵。实际上,最简单的置换矩阵P就是单位矩阵I本身,他的作用就是对矩阵不做任何处理,即:
P = I(no exchanges)
为了更加直观的描述一个置换矩阵的功能,我们可以用矩阵来表示置换矩阵。用去左乘另一个矩阵,会交换这个矩阵I的i行和j行。如果我们仔细比较置换矩阵中的i,j行和相同尺寸的单位矩阵中的i,j行,我们会发现,他就是交换了单位矩阵中ij行后的矩阵。

置换矩阵的性质
1,对任何一个置换矩阵P而言,每一行,梅一列都只有一个“1”。
2,同时,置换矩阵的转置也是一个置换矩阵,可能是同一个矩阵P,可能是另一个矩阵。
3,任意两个置换矩阵的乘积也是一个置换矩阵。
置换矩阵也可以是一次交换多行的矩阵P,这需要通过两个置换矩阵相乘得到:
例子:

4,对于任何n阶矩阵,共有n的阶乘种置换矩阵。其中,n!=1x2x3...xn。因此,若n=4就对应有24种置换矩阵,若n=5,就会有120种置换矩阵!
5,置换矩阵的逆矩阵就是他自己。已知,置换矩阵的作用就是交换另一个矩阵的i行和j行,要想恢复这个操作,那就是把另一个矩阵的i行和j行再交换一次,所以:
注意,第五条所说的性质,只争对进行一次行交换的置换矩阵,但,如果是一次执行多次行交换的置换矩阵,例如P=P21P32,他的矩阵和他的逆不同,如下:


但他的逆确实实现了对p操作的还原,如下:

6,置换矩阵被广泛的用于对非奇异矩阵(nonsingular matrix)进行高斯消元时,遇到主元为零时需要进行行交换的情况。即:PA=LU(或者PA=LDU)。对于奇异矩阵(singular matrix),行交换也无法彻底杜绝主元为0的情形。
By the way: LU分解是一个伟大的矩阵分解!
以下是一些早期的个人笔记:
置换矩阵:

置换矩阵的乘法:

置换矩阵的性质:

注:上文中提到的,置换矩阵P可用于列交换,需要进一步考证,待定!
(全文完)
作者 --- 松下J27
格言摘抄:人就是三个口!(无名氏)
参考文献(鸣谢):
文中截图均来自于:《Introduction to Linear Algebra》,5th Edition - Gilbert Strang

(配图与本文无关)文章来源:https://www.toymoban.com/news/detail-455114.html
版权声明:所有的笔记,可能来自很多不同的网站和说明,在此没法一一列出,如有侵权,请告知,立即删除。欢迎大家转载,但是,如果有人引用或者COPY我的文章,必须在你的文章中注明你所使用的图片或者文字来自于我的文章,否则,侵权必究。 ----松下J27文章来源地址https://www.toymoban.com/news/detail-455114.html
到了这里,关于线性代数 --- 置换矩阵 (Permutation matrix)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!