目录
1. 概要
2. 二叉树的序列化
2.1 基于前序遍历的序列化
2.2 基于后序遍历的序列化
2.3 基于层序遍历的序列化
3. python实现
3.1 二叉树节点的表示
3.2 层序遍历序列化的python实现
3.3 层序遍历反序列化的python实现
3.4 测试
1. 概要
本文简要介绍二叉树的序列化处理和反序列化处理及对应的python实现。
二叉树通常为了方便而以一维数组(比如说python list)的格式进行存储,二叉树的序列化(serialization)就是指将二叉树转换成列表或者一维数组的形式(或者说线性化表示)。实际使用的时候再由列表的形式变换回二叉树的格式,这个就是反序列化(de-serialization)。
当然,更彻底的序列化和反序列化:Serialization is translating a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network. In the future, we can deserialize the sequence to reconstruct the same data structure or object. 即将一个数据结构或者对象转换为字节或甚至比特流,以方便存储和传输,并且要能够在需要使用的时候进行恢复。但是,由于转换为一维数组表示是进一步转换为字节流或这比特流的前提和必经之路,也是序列化的最关键的步骤,本文只讨论序列化到一维数组以及对饮的反序列化处理。
序列化和反序列化是各种复杂的数据结构的实际存储和使用时都需要碰到的问题。
2. 二叉树的序列化
二叉树的序列化的基本处理就是二叉树的层序遍历,而二叉树的遍历常用方法有以下几种:前序遍历,中序遍历,后序遍历,层序遍历。除了中序遍历外,其余三种遍历方法都可以实现二叉树的序列化,即得到二叉树的一维数组表示。
虽然遍历是序列化处理的底层处理,但是,序列化又不仅仅是遍历。一个常见的误解是将二叉树进行遍历展开就得到了二叉树的一维数组表示。其实不是,单纯地对二叉树进行得到的列表无法还原成原始的二叉树。

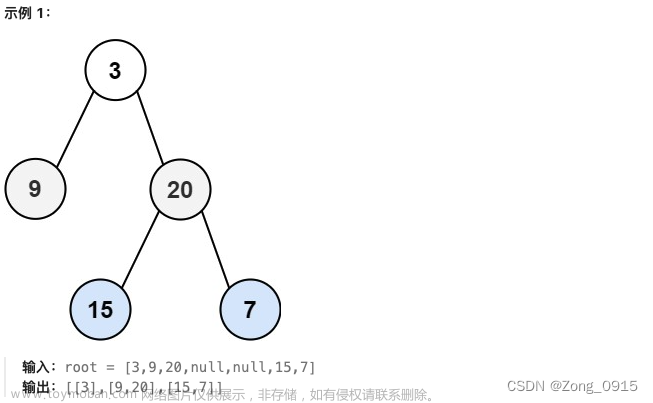
上图这个不完全的二叉树直接进行层序遍历得到的是[1,2,-3,-5,4],实际上它的一维数组表示为[1,2,-3,-5,null,4,null]。
只有完全二叉树的常规遍历能够得到其序列化表示。所以,对于一般的(不完全)二叉树,其序列化处理可以考虑先将其补全为完全二叉树,不存在的节点用Null或None填充,然后再对该完全二叉树进行遍历即可。但是实际实现时不会去先执行Null或None填充,而是一边遍历一边执行Null或None填充。如下图所示:

前序遍历和后序遍历和层序遍历都可以实现序列化,只要序列化和反序列化对称。但是中序遍历不适合于序列化实现。
We cannot use the in-order tree traversal method to serialize and deserialize a binary tree. In an in-order binary tree traversal, we traverse the left subtree first. Then, we visit the root node and traverse the right subtree. This traversal makes it hard to locate the root node in the serialized sequence. For example, an in-order traversal of the following binary tree can produce a sequence: #,2,#,1,#:

However, we can produce the same in-order sequence on the following binary tree:

也就是说,基于中序遍历可能存在不同的二叉树得到相同的序列化表示,这样就使得反序列化无法唯一地恢复原二叉树。因此,中序遍历不适合于序列化实现。
2.1 基于前序遍历的序列化
如下所示为一个递归方式实现的前序遍历序列化处理。

In this algorithm, we first serialize the root node data, then recursively serialize its left and right children. If we meet a null node, we also serialize it with a special character #.
该算法的时间复杂度为O(n),因为每个节点只访问一次。空间复杂度(平均意义上来说)也是O(n),就是存储输出序列。注意,对于深度为k的完全二叉树,总共有个节点。最极端情况下,k个节点排成k层不完全二叉树,而且每一层的节点都是上一层的右子节点,那么在基于前序遍历的序列化处理后,需要 长度为的数组表示。
与此对应的反序列化算法流程如下所示:

前序遍历的顺序是先处理根节点,然后是左子树,最后是右子树。反序列化时则是相反的顺序,即先处理右子树,然后是左子树,最后是根节点。
2.2 基于后序遍历的序列化
同理可以得到基于后序遍历的序列化和反序列化算法流程如下所示:


后序遍历的顺序是先处理左子树,然后是右子树,最后是根节点。反序列化时则是相反的顺序,即先处理根节点,然后是右子树,最后是左子树。
2.3 基于层序遍历的序列化
基于层序遍历得到的二叉树的一维数组表示的基本规则是(为了方便,记该数组为a,0-indexing,并且采用python slicing的方式表示子数组):
(1) a[0]表示根节点
(2) a[2**k-1 : 2**(k+1)-1]表示层k(1,2,...)的节点(假定根节点位于层0)
(3) 每一层中的节点按从左到右排列
(4) 不存在(作为完全二叉树应该有但是实际上不存在)的节点用None或者Null填充
(5) 最后的连续的None可以去除
3. python实现
3.1 二叉树节点的表示
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right每个二叉树的节点最都有两个子节点,分别为左子节点和右子节点。以上类定义中,分别用left和right指向左子节点和右子节点。
3.2 层序遍历序列化的python实现
实现思路:to be added
def binTree2Lst(root):
"""
binary tree serialization.
Convert a binary tree with "root" as its root to a list.
"""
if root == None:
return []
nodeLst = [root]
valLst = []
while len(nodeLst) > 0:
curNode = nodeLst.pop()
if curNode != None:
nodeLst.insert(0,curNode.left)
nodeLst.insert(0,curNode.right)
valLst.append(curNode.val)
else:
valLst.append(None)
# Throw away the trailing 'None'
while valLst[-1] == None:
valLst.pop()
return valLst3.3 层序遍历反序列化的python实现
实现思路:to be added
def lst2bintree(x:List[int]) -> Optional[TreeNode]:
if len(x) == 0: # []
root = None
if x[0] == None: # [None]
root = None
x.reverse() # For the convenience of utilizing x.pop()
nodeLoL = []
root = TreeNode(x.pop())
nodeLoL.append([root])
k = 0
while(1):
#print('k = {0}, {1}'.format(k, x))
newLayer = []
for node in nodeLoL[k]:
#print(node.val)
if node == None:
pass
else:
if len(x) == 0:
break
tmp = x.pop()
if tmp != None:
newNode = TreeNode(tmp)
node.left = newNode
newLayer.append(newNode)
if len(x) == 0:
break
tmp = x.pop()
if tmp != None:
newNode = TreeNode(tmp)
node.right = newNode
newLayer.append(newNode)
if len(x) == 0:
break
nodeLoL.append(newLayer)
k += 1
return root3.4 测试
x = [3,9,20,None,None,15,7]
root = lst2bintree(x)
print(root.val)
print(root.left.val)
print(root.right.val)
print(root.left.left)
print(root.left.right)
print(root.right.left.val)
print(root.right.right.val)
print(binTree2Lst(root))
x = [1,2,-3,-5,None,4,None]
root = lst2bintree(x)
print(binTree2Lst(root))运行结果如下:
3
9
20
None
None
15
7
[3, 9, 20, None, None, 15, 7] 文章来源:https://www.toymoban.com/news/detail-456282.html[1, 2, -3, -5, None, 4]文章来源地址https://www.toymoban.com/news/detail-456282.html
到了这里,关于二叉树的序列化(serialization)与反序列化(de-serialization)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!