导言:
在最优化问题中,找到函数的最小值或最大值是一个重要的任务。牛顿法是一种经典的迭代方法,常用于优化问题的求解。本文将详细介绍最优化方法中的牛顿法一维搜索,包括其基本原理、算法步骤以及应用场景。
一、牛顿法概述
牛顿法,也称为牛顿-拉夫逊方法,是一种迭代的优化算法,用于求解非线性函数的极值点。它通过利用函数的二阶导数信息来逼近极值点,并在每次迭代中更新搜索方向,以快速收敛到最优解。
二、牛顿法一维搜索原理
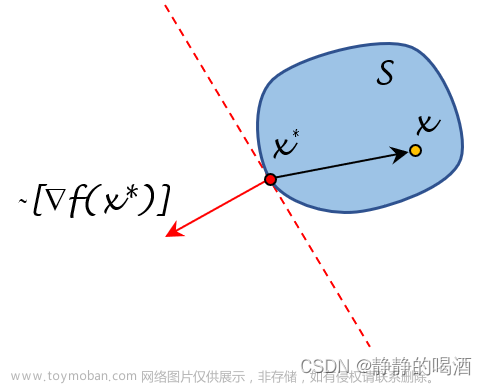
在一维搜索中,我们希望找到函数在某个特定方向上的最小值点。牛顿法通过在当前点处利用函数的一阶和二阶导数信息,来确定搜索方向和步长。
具体步骤如下:
1. 初始化:选择初始点x0,并设定迭代终止条件,如迭代次数或函数值的收敛阈值。
2. 计算一阶和二阶导数:计算函数f(x)在当前点xk处的一阶导数f'(xk)和二阶导数f''(xk)。
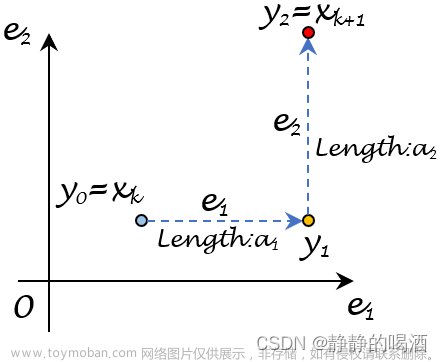
3. 更新搜索方向和步长:根据二阶导数的信息,计算搜索方向dk和步长αk。
4. 更新当前点:计算新的点xk+1 = xk + αk * dk。
5. 判断终止条件:检查是否满足终止条件,如果满足则停止迭代,否则返回步骤2。
三、牛顿法一维搜索的优势
牛顿法一维搜索具有以下优势:
1. 收敛速度快:由于利用了二阶导数的信息,牛顿法能够更准确地逼近最优解,因此通常具有较快的收敛速度。
2. 鲁棒性强:牛顿法对初始点的选择不敏感,能够在大多数情况下找到良好的最优解。
3. 适用范围广:牛顿法不仅适用于凸函数,还适用于非凸函数的优化问题。
四、牛顿法一维搜索的应用场景
牛顿法一维搜索广泛应用于各种最优化问题中,特别是对于高维优化问题的求解具有重要意义。以下是一些常见的应用场景:
1. 机器学习中的参数
优化:在训练模型的过程中,需要对参数进行优化,牛顿法一维搜索可以用于更新参数的值,以最小化损失函数。
2. 信号处理中的峰值检测:牛顿法一维搜索可以用于检测信号中的峰值,从而确定峰值的位置和强度。
3. 金融领域中的投资组合优化:在投资组合优化中,可以使用牛顿法一维搜索来确定资产权重,以最大化投资组合的预期收益或最小化风险。
注:本文中的牛顿法一维搜索仅为最优化方法中的一小部分内容,对于完整的牛顿法和优化算法体系,仍需深入学习和研究。
当使用牛顿法进行一维搜索时,需要注意以下几个方面:
1. 初始点的选择:牛顿法对于初始点的选择并不敏感,通常可以选择函数定义域中的任意一点作为初始点开始迭代。然而,对于某些特殊的函数或问题,初始点的选择可能会影响最终的收敛性和结果。
2. 导数计算:牛顿法需要计算函数的一阶导数和二阶导数。这可以通过解析求导或数值求导来实现。如果函数具有解析求导的形式,则可以直接计算导数。否则,可以使用数值方法,如有限差分法,来近似计算导数。
3. 二阶导数的正定性检查:在牛顿法中,二阶导数矩阵(海森矩阵)被用于确定搜索方向和步长。在迭代过程中,需要检查二阶导数矩阵的正定性。如果二阶导数矩阵不是正定的,可能导致算法无法收敛或收敛到局部最小值。在这种情况下,可以采取调整步长或使用其他优化方法的策略来解决问题。
4. 迭代终止条件:为了控制迭代的次数和达到预定的精度要求,需要设定合适的迭代终止条件。常见的终止条件包括迭代次数的限制、目标函数值的收敛阈值或参数变化的阈值等。
5. 非凸函数的处理:牛顿法在处理非凸函数时可能存在局部最优的问题。在实际应用中,为了避免陷入局部最优,可以结合其他优化算法或采用多次随机初始点的策略。
总结:
牛顿法一维搜索是最优化方法中的重要工具,通过利用函数的一阶和二阶导数信息,能够快速逼近最优解。在使用牛顿法进行一维搜索时,需要注意初始点的选择、导数的计算、二阶导数的正定性检查、迭代终止条件的设定以及非凸函数的处理。了解并灵活运用这些注意事项,将有助于更有效地应用牛顿法进行一维搜索,从而解决实际问题。
以下是使用Python、MATLAB、R和Java实现最优化方法中的牛顿法一维搜索的示例代码:文章来源:https://www.toymoban.com/news/detail-456547.html
Python代码示例:
import numpy as np
def newton_1d_search(f, f_prime, f_double_prime, x0, max_iterations=100, tol=1e-6):
x = x0
for _ in range(max_iterations):
f_prime_val = f_prime(x)
f_double_prime_val = f_double_prime(x)
if np.abs(f_prime_val) < tol:
break
x = x - f_prime_val / f_double_prime_val
return x
# 示例函数:f(x) = x^2 - 4
def f(x):
return x**2 - 4
# 示例函数的一阶导数:f'(x) = 2x
def f_prime(x):
return 2 * x
# 示例函数的二阶导数:f''(x) = 2
def f_double_prime(x):
return 2
# 测试代码
x0 = 1 # 初始点
result = newton_1d_search(f, f_prime, f_double_prime, x0)
print("Optimal solution:", result)MATLAB代码示例:
function result = newton_1d_search(f, f_prime, f_double_prime, x0, max_iterations, tol)
x = x0;
for i = 1:max_iterations
f_prime_val = f_prime(x);
f_double_prime_val = f_double_prime(x);
if abs(f_prime_val) < tol
break;
end
x = x - f_prime_val / f_double_prime_val;
end
result = x;
end
% 示例函数:f(x) = x^2 - 4
f = @(x) x^2 - 4;
% 示例函数的一阶导数:f'(x) = 2x
f_prime = @(x) 2 * x;
% 示例函数的二阶导数:f''(x) = 2
f_double_prime = @(x) 2;
% 测试代码
x0 = 1; % 初始点
max_iterations = 100; % 最大迭代次数
tol = 1e-6; % 收敛阈值
result = newton_1d_search(f, f_prime, f_double_prime, x0, max_iterations, tol);
disp("Optimal solution: " + result);R代码示例:
newton_1d_search <- function(f, f_prime, f_double_prime, x0, max_iterations = 100, tol = 1e-6) {
x <- x0
for (i in 1:max_iterations) {
f_prime_val <- f_prime(x)
f_double_prime_val <- f_double_prime(x)
if (abs(f_prime_val) < tol) {
break
}
x <- x - f_prime_val / f_double_prime_val
}
return(x)
}
# 示例函数:f(x) = x^2 - 4
f <- function(x) {
return(x^2 - 4)
}
# 示例函数的一阶导数:f'(x) = 2x
f_prime <- function(x) {
return(2 * x)
}
# 示例函数的二阶导数:f''(x) = 2
f_double
_prime <- function(x) {
return(2)
}
# 测试代码
x0 <- 1 # 初始点
result <- newton_1d_search(f, f_prime, f_double_prime, x0)
cat("Optimal solution:", result, "\n")Java代码示例:
public class Newton1DSearch {
public static double newton1DSearch(DoubleFunction<Double> f, DoubleFunction<Double> fPrime,
DoubleFunction<Double> fDoublePrime, double x0, int maxIterations, double tol) {
double x = x0;
for (int i = 0; i < maxIterations; i++) {
double fPrimeVal = fPrime.apply(x);
double fDoublePrimeVal = fDoublePrime.apply(x);
if (Math.abs(fPrimeVal) < tol) {
break;
}
x = x - fPrimeVal / fDoublePrimeVal;
}
return x;
}
public static void main(String[] args) {
// 示例函数:f(x) = x^2 - 4
DoubleFunction<Double> f = x -> x * x - 4;
// 示例函数的一阶导数:f'(x) = 2x
DoubleFunction<Double> fPrime = x -> 2 * x;
// 示例函数的二阶导数:f''(x) = 2
DoubleFunction<Double> fDoublePrime = x -> 2.0;
// 测试代码
double x0 = 1; // 初始点
int maxIterations = 100; // 最大迭代次数
double tol = 1e-6; // 收敛阈值
double result = newton1DSearch(f, fPrime, fDoublePrime, x0, maxIterations, tol);
System.out.println("Optimal solution: " + result);
}
}请注意,以上代码仅为示例,可能需要根据实际问题进行适当的修改和调整。此外,MATLAB和R的示例中使用的函数句柄和函数定义方式可能略有不同,具体取决于使用的版本和环境。文章来源地址https://www.toymoban.com/news/detail-456547.html
到了这里,关于最优化方法-牛顿法一维搜索的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!