一、问题背景简介

相传在古印度圣庙中,有一种被称为汉诺塔(Hanoi)的游戏。该游戏是在一块铜板装置上,有三根杆(编号A、B、C),在A杆自下而上、由大到小按顺序放置64个金盘(如图1)。游戏的目标:把A杆上的金盘全部移到C杆上,并仍保持原有顺序叠好。操作规则:每次只能移动一个盘子,并且在移动过程中三根杆上都始终保持大盘在下,小盘在上,操作过程中盘子可以置于A、B、C任一杆上。
二、解题思路
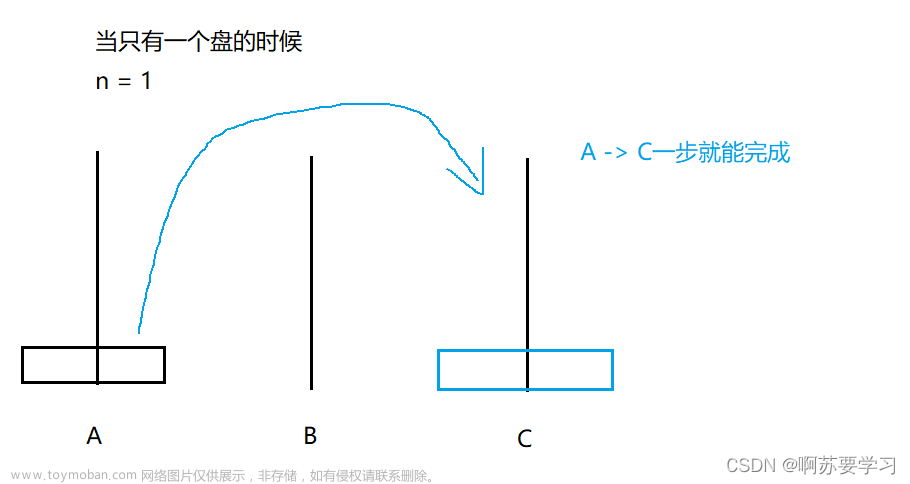
首先我们需要先明确我们每一步的目的,这里我们自底向上来进行思考,首先我们我们想到如果我们要将A上的所有盘子移动到C上,又得随时保证大盘子在下面小盘子在上面,那么我们开始思考如何将最大的盘子先放到C上,这样才能进行下一步。
我们先明确ABC三个柱子的角色,一个作为起始位置、一个作为中转的位置、一个是目的位置;我们开始从最大的盘子开始自底向上考虑,这里我用四个盘子来做例子:
①我们要将第四个盘子移动到C,那么前三个盘子就必须先移动到B,这样才能让第四个盘子直接移动到C(因为要移动最下面的盘子的话,必须整个柱子只剩它一个或者它在最上层才能移动);
②要将前三个盘子移动到B,第三个盘子就要在B的最下面,现在就将第三个盘子看做底,那么肯定前两个盘子就要先移动到C,这样第三个盘子才能直接移动到B;
③要将前两个盘子移动到C,那么第二个盘子就必须在C的最下面,现在将第二个盘子看做底,那么第一个盘子就必须先移动到B,这样第二个盘子才能直接移动到C;
④第一个盘子可以直接移动到B;
以上就是有四个盘子的时候第一步的思考,思考过程反过来就是移动步骤;每一步中的移动的思维就差不多;在同一层递归的整体的步骤就是:先将要移动的盘子上面的盘子放到中转的位置去,然后再把要移动的盘子放到目标位置去,最后将中转的位置的盘子再放到目标位置就完成了;每移动一次目标盘子,就需要执行一次以上步骤,因为我们移动的整体思路是自下而上的移动,所以只有当移动的盘子是最顶上的盘子或者只有它一个盘子的时候不需要执行这个三步;所以只要涉及到移动多个盘子就需要进行上述步骤,所以在每层递归中一开始的当前位置到中转,和最后的中转到目标位置,都需要递归执行,只有中间的当前位置直接到目标位置的这一步只移动一个盘子不需要递归。
三、代码实现展示
1、Python实现
def Hanoi(n, current, transit, target):
if n == 1:
print(current, "-->", target)
else:
Hanoi(n - 1, current, target, transit)
print(current, "-->", target)
Hanoi(n - 1, transit, current, target)
num = input("输入汉诺塔的层数:")
Hanoi(num, 'A', 'B', 'C')这里需要注意一下递归的时候当前位置、中转位置、以及目标位置的转变(实参、形参的变化)。文章来源:https://www.toymoban.com/news/detail-458019.html
2、C语言实现
#include "stdio.h"
void Hanoi(int n,char current,char transit,char target){
if(n == 1){
printf("%c-->%c\n",current,target);
} else{
Hanoi(n - 1,current,target,transit);
printf("%c-->%c\n",current,target);
Hanoi(n - 1,transit,current,target);
}
}
int main() {
int n;
printf("请输入汉诺塔的层数:");
scanf("%d",&n);
Hanoi(n,'A','B','C');
}基本和python差不多。文章来源地址https://www.toymoban.com/news/detail-458019.html
到了这里,关于经典递归算法——汉诺塔问题的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!