( 动态规划) 516. 最长回文子序列 ——【Leetcode每日一题】-Toy模板网

这篇具有很好参考价值的文章主要介绍了( 动态规划) 516. 最长回文子序列 ——【Leetcode每日一题】。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

❓516. 最长回文子序列

难度：中等

给你一个字符串 s ，找出其中最长的回文子序列，并返回该序列的长度。

子序列定义为：不改变剩余字符顺序的情况下，删除某些字符或者不删除任何字符形成的一个序列。

示例 1：

输入：s = “bbbab”
输出：4
解释：一个可能的最长回文子序列为 “bbbb” 。

示例 2：

输入：s = “cbbd”
输出：2
解释：一个可能的最长回文子序列为 “bb” 。

提示：

1 <= s.length <= 1000
s 仅由小写英文字母组成

💡思路：动态规划

对于一个子序列而言，如果它是回文子序列，并且长度大于 2，那么将它首尾的两个字符去除之后，它仍然是个回文子序列。因此可以用动态规划的方法计算给定字符串的最长回文子序列。

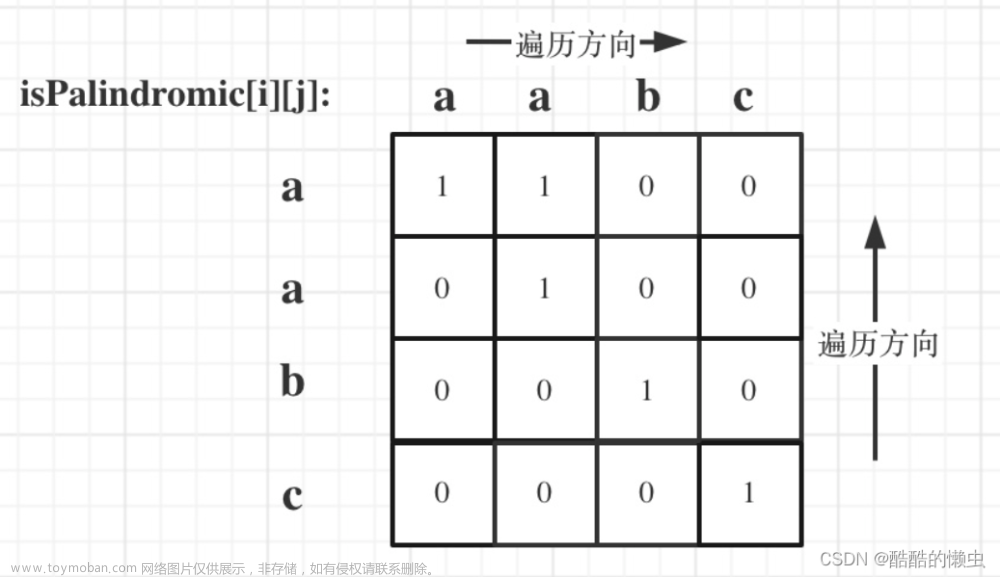
定义二维dp数组，dp[i][j] 表示字符串 s 的下标范围 [i,j] 内的最长回文子序列的长度。假设字符串 s 的长度为 n，则只有当 0 ≤ i ≤ j < n 时，才会有 dp[i][j] > 0，否则 dp[i][j] = 0。

当 i < j 时，计算 dp[i][j] 需要分别考虑 s[i] 和 s[j] 相等和不相等的情况：

如果 s[i] = s[j]，则首先得到 s 的下标范围 [i + 1, j − 1] 内的最长回文子序列，然后在该子序列的首尾分别添加 s[i] 和 s[j]，即可得到 s 的下标范围 [i,j] 内的最长回文子序列，因此 :
$\textit{dp}[i][j] = \textit{dp}[i+1][j-1] + 2$
如果 s[i] ≠ s[j]，则 s[i] 和 s[j] 不可能同时作为同一个回文子序列的首尾，因此：
$\textit{dp}[i][j] = \max(\textit{dp}[i+1][j], \textit{dp}[i][j-1])$

由于状态转移方程都是从长度较短的子序列向长度较长的子序列转移，因此需要注意动态规划的循环顺序。

( 动态规划) 516. 最长回文子序列 ——【Leetcode每日一题】

最终得到 dp[0][n−1] 即为字符串 s 的最长回文子序列的长度。

⭐️ 空间优化：

观察发现 dp[i][j] 只与dp[i][j-1] 以及第 i + 1行有关系，所以可以进行空间优化，只需要两个一维数组，分别为 fir 和 sec ,交替滚动即可，此时的状态转移方程为：

若s[i] = s[j] :
$\textit{dp}[fir][j] = \textit{dp}[sec][j-1] + 2$
如果 s[i] ≠ s[j]，则 s[i] 和 s[j] 不可能同时作为同一个回文子序列的首尾，因此：
$\textit{dp}[fir][j] = \max(\textit{dp}[sec][j], \textit{dp}[fir][j-1])$

🍁代码：(Java、C++)

Java

public class Solution {
    public int longestPalindromeSubseq(String s) {
        int n = s.length();
        int[][] dp = new int[n][n];
        for (int i = n - 1; i >= 0; i--) { // 从后往前遍历 保证情况不漏
            dp[i][i] = 1; // 初始化
            for (int j = i + 1; j < n; j++) {
                if (s.charAt(i) == s.charAt(j)) {
                    dp[i][j] = dp[i + 1][j - 1] + 2;
                } else {
                    dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[0][n - 1];
    }
}

C++

class Solution {
public:
    int longestPalindromeSubseq(string s) {
        int n = s.size();
        vector<vector<int>> dp(n, vector<int>(n));
        for (int i = n - 1; i >= 0; i--) { // 从后往前遍历 保证情况不漏
            dp[i][i] = 1; // 初始化
            for (int j = i + 1; j < n; j++) {
                if (s[i] == s[j]) {
                    dp[i][j] = dp[i + 1][j - 1] + 2;
                } else {
                    dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[0][n - 1];
    }
};

⭐️ 空间优化：
Java

public class Solution {
    public int longestPalindromeSubseq(String s) {
        int n = s.length();
        int[][] dp = new int[2][n];
        int fir = 0, sec = 1;
        for (int i = n - 1; i >= 0; i--) { // 从后往前遍历 保证情况不漏
            dp[fir][i] = 1; // 初始化
            for (int j = i + 1; j < n; j++) {
                if (s.charAt(i) == s.charAt(j)) {
                    dp[fir][j] = dp[sec][j - 1] + 2;
                } else {
                    dp[fir][j] = Math.max(dp[sec][j], dp[fir][j - 1]);
                }
            }
            int tmp = fir;
            fir = sec;
            sec = tmp;
        }
        return Math.max(dp[0][n - 1], dp[1][n - 1]);
    }
}

C++

class Solution {
public:
    int longestPalindromeSubseq(string s) {
        int n = s.size();
        vector<vector<int>> dp(2, vector<int>(n));
        int fir = 0, sec = 1;
        for (int i = n - 1; i >= 0; i--) { // 从后往前遍历 保证情况不漏
            dp[fir][i] = 1; // 初始化
            for (int j = i + 1; j < n; j++) {
                if (s[i] == s[j]) {
                    dp[fir][j] = dp[sec][j - 1] + 2;
                } else {
                    dp[fir][j] = max(dp[sec][j], dp[fir][j - 1]);
                }
            }
            int tmp = fir;
            fir = sec;
            sec = tmp;
        }
        return max(dp[0][n - 1], dp[1][n - 1]);
    }
};