MATLAB数学建模：数据图形可视化-三维绘图函数-Toy模板网

这篇具有很好参考价值的文章主要介绍了MATLAB数学建模：数据图形可视化-三维绘图函数。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

1 绘制三维曲面

在 MATLAB 中, 我们可使用函数 surf 和 surfc 绘制三维曲面图. 调用格式如下:

surf(Z)
surf(X,Y,Z)
surf(X,Y,Z,C)
surf(...,'PropertyName',PropertyValue)
surfc(...)

以矩阵 ZZZ 所指定的参数创建一个渐变的三维曲面. 坐标 $x = 1:n,\ \ y = 1:m, $ 其中 [m,n]=size(Z)[m,n] = size(Z)[m,n]=size(Z)
以 ZZZ 确定的曲面高度和颜色, 按照 X,YX,YX,Y 形成的格点矩阵, 创建一个渐变的三维曲面. X,YX,YX,Y 可为向量或矩阵, 若 X,YX,YX,Y 为向量, 则必须满足 m=size(X),n=size(Y),[m,n]=size(Z).m = size(X), n=size(Y), [m,n] = size(Z).m=size(X),n=size(Y),[m,n]=size(Z).
以 ZZZ 确定的曲面高度, CCC 确定的曲面颜色, 按 X,YX,YX,Y 形成的格点矩阵创建一个渐变的三维曲面.
设置曲面属性.
在曲面下绘制曲面的等高线.

注:

在图形窗口, 需要将图形属性 Render 设为 Painters, 才可以显示出坐标名称和图形标题.

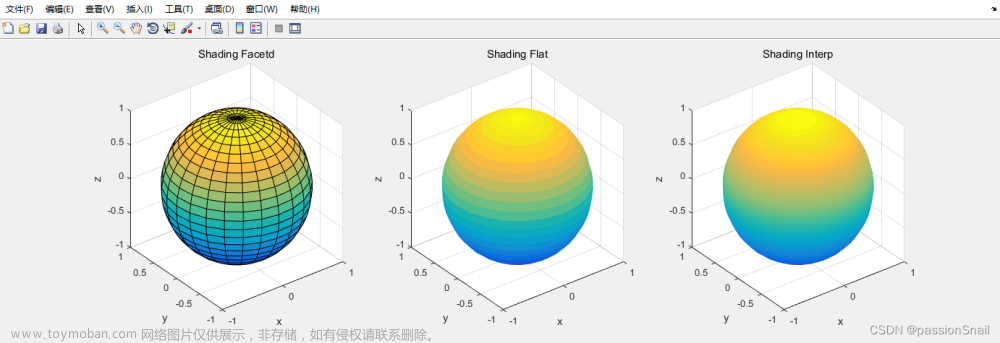
图中可见, 球面被网格线分割成多块. 每一块可视为一块嵌在线条之间的补片, 这些线条和补片的渐变颜色可由命令 shading 所指定. 格式为:

shading faceted
shading flat
shading interp

默认值, 在绘制曲面时采用分层网格线.
不绘制线条, 补片颜色单一, 颜色平滑分布.
不绘制线条, 补片以插值加色, 颜色以插补式分布, 计算量更大.

[例]

绘制三维球体.

[X,Y,Z] = sphere(25);         %计算球体的三维坐标
subplot(1,3,1);
surf(X,Y,Z)                   %绘制球体的三维图形
xlabel('x');
ylabel('y');
zlabel('z');
title('Shading Facetd');subplot(1,3,2);
surf(X,Y,Z)                   
xlabel('x');
ylabel('y');
zlabel('z')
shading flat;
title('Shading Flat');subplot(1,3,3);
surf(X,Y,Z)                   
xlabel('x');
ylabel('y');
zlabel('z');
shading interp;
title('Shading Interp');

图形输出如下:

除了 surf 和 surfc 函数以外, 还可以使用下列函数绘制不同的三维曲面:

使用 sphere 函数绘制三维球面. 调用格式为:

[x,y,z] = sphere(n)     %n为球面的光滑程度, 默认值为20

使用 cylinder 函数绘制三维柱面. 调用格式为:

[x,y,z] = cylinder(R,n) 
%R为存放柱面各等间隔高度上半径的向量, n表示圆柱圆周上等间隔点个数, 默认为20.

2 生成栅格数据

栅格数据指按照网格单元的行列排列, 具有不同灰度或颜色的数据阵列. 每个单元的位置由其行列号定义, 所表示的实际位置含于栅格行列位置中. 数据组织中的每个数据表示事物或现象的非几何属性, 或指向其属性的指针.

在绘制网格曲面前, 必须先知道每个四边形顶点的三维坐标值. 绘制曲面的一般情况是: 先知道四边形每个顶点的二维坐标(x,y), 再利用某个函数公式计算出四边形各个顶点的 zzz 坐标.

此处使用的 (x,y)(x,y)(x,y) 二维坐标是一种栅格形的数据点, 可由 MATLAB 所提供的 meshgrid 函数产生. 调用格式为;

[X,Y] = meshgrid(x,y)

该命令功能是由 xxx 向量和 yyy 向量通过复制的方法产生绘制三维图形时所需的栅格数据: XXX 和 YYY 矩阵.

注:

向量 x,yx,yx,y 分别代表三维图形在 XXX 轴, YYY 轴方向上的取值数据点.

x,yx,yx,y 分别是向量, 而 X,YX,YX,Y 是矩阵.

我们还可以使用函数 georasterref 命令绘制栅格数据. 调用格式如下;

R = georasterref()

[例]

使用地理栅格数据绘制经纬度曲线:

maps                       %查看当前可用的投影方式%% 导入数据:全球海岸线
load coast%% 绘图
axesm robinson
patchm(lat,long,'g');%% 设置属性
setm(gca);                  %查看当前可设置的所有图形坐标轴的属性
setm(gca,'Frame','on');     %使框架可见
getm(gca,'Frame');          %使用getm可以获取指定的图形坐标轴的属性
setm(gca,'Grid','on');      %打开网格
setm(gca,'MLabelLocation',180);         %标上经度刻度标签,每隔60度
setm(gca,'MeridianLabel','on');         %设置纬度刻度标签可见
setm(gca,'PLabelLocation',[-90:90:90]); %标上纬度刻度标签
setm(gca,'ParallelLabel','on');         %设置经度刻度标签可见
setm(gca,'MLabelParallel','south')      %将经度刻度标签放在下部(南方)
setm(gca,'Origin',[0,90,0]);            %设置地图中心位置和绕中心点的轴旋转角度

输出图形如下:

3 绘制网格曲面命令

MATLAB 中可通过 mesh 函数绘制三维网格曲面图. 该函数可生成指定的网线面和它的颜色. 函数调用格式如下:

mesh(X,Y,Z)
mesh(Z)
mesh(...,C)
mesh(..., PropertyName, PropertyValue, ...)
h = mesh(...)

绘制出颜色由 X,Y,ZX,Y,ZX,Y,Z 指定的网线面. 若 X,YX,YX,Y 均为向量, length(X) = n, length(Y) = m, [m,n] = size(Z) , 空间中的点 (X(j),Y(I),Z(I,j))(X(j),Y(I),Z(I,j))(X(j),Y(I),Z(I,j)) 为所绘制曲面网线的交点.
由[n,m]= size(Z) 得 X = 1:n, Y = 1:m, 其中 zzz 为定义在矩形划分区域上的单值函数.
用由矩阵 CCC 所指定的颜色绘制网线网格图.
对指定的属性 PropertyName 设定属性值 PropertyValue ,可在同一语句中对多个属性进行设置.
返回 surface 图形对象句柄.

函数 mesh 运算规则为:

确定数据 X,Y,ZX,Y,ZX,Y,Z 的范围. 可使用命令 axis 对当前轴的 XLinMode,YLinMode,ZLinMode 进行设置.

参量 CCC 的范围决定颜色的"刻度化程度".

网格图显示命令生成将 ZZZ 的数据值用当前色图表现出来的颜色值.

[例]

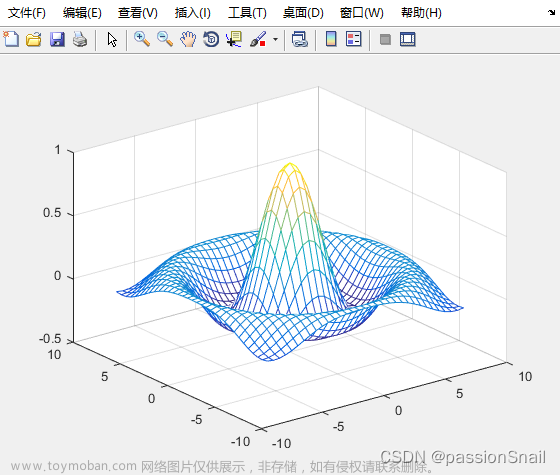
在 Descartes 坐标系中绘制下列函数的网格曲面图:

f(x,y)=sin(x2+y2)x2+y2f(x,y) = \frac{sin(\sqrt{x^{2} + y^{2}})}{\sqrt{x^{2} + y^{2}}}f(x,y)=x2+y2sin(x2+y2)

x = -8:0.5:8;
y = x;
[X,Y] = meshgrid(x,y);
R = sqrt(X.^2 + Y.^2) + eps;
Z = sin(R)./R;
mesh(X,Y,Z)
grid on

图形输出如下:

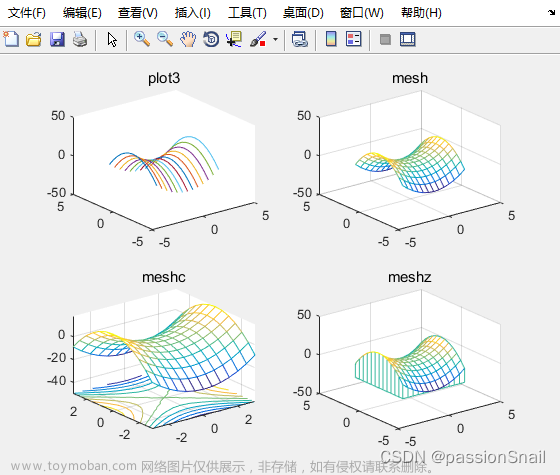
此外, MATLAB还有两个 mesh 函数的派生函数:

meshc: 同时在 x−yx-yx−y 平面上绘制函数的等值线.

meshz: 在网格图基础上, 在图形底部外侧绘制 zzz 轴边框线.

[例]

[X,Y] = meshgrid(-3:0.5:3);
Z = 2*X.^2 - 3*Y.^2;
subplot(2,2,1)
plot3(X,Y,Z)
title('plot3')
subplot(2,2,2)
mesh(X,Y,Z)
title('mesh')
subplot(2,2,3)
meshc(X,Y,Z)
title('meshc')
subplot(2,2,4)
meshz(X,Y,Z)
title('meshz')

图形输出如下;

4 隐藏线的显示和关闭

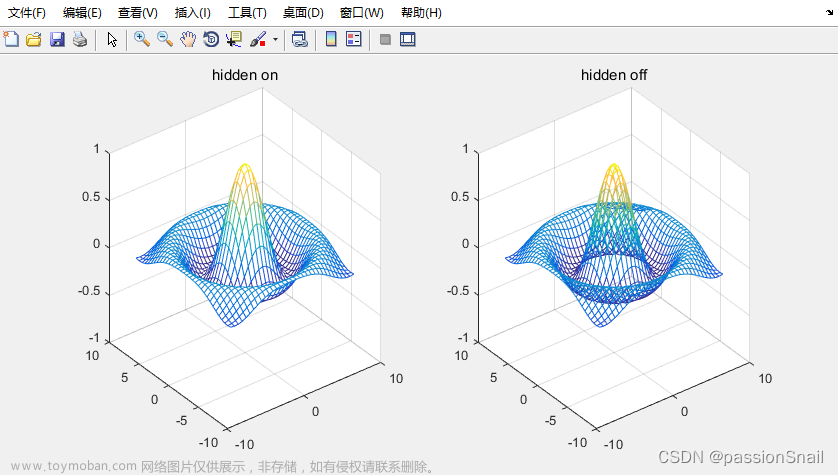
是否显示网格曲面的隐藏线会对图形显示效果产生一定影响. MATLAB 提供了相关控制命令 hidden , 调用这种命令的格式为 hidden on 或 hidden off, 用于开启/关闭网格曲面的隐藏线.

[例]

分别绘制有无隐藏线的函数:

f(x,y)=sin(x2+y2)x2+y2f(x,y) = \frac{sin(\sqrt{x^{2} + y^{2}})}{\sqrt{x^{2} + y^{2}}}f(x,y)=x2+y2sin(x2+y2)

网格曲面图.

x = -8:0.5:8;
y = x;
[X,Y] = meshgrid(x,y);
R = sqrt(X.^2 + Y.^2) + eps;
Z = sin(R)./R;
subplot(1,2,1)
mesh(X,Y,Z)
grid on
hidden on
title('hidden on')
axis([-10 10 -10 10 -1 1])subplot(1,2,2)
mesh(X,Y,Z)
grid on
hidden off
title('hidden off')
axis([-10 10 -10 10 -1 1])

图形输出如下:文章来源地址https://www.toymoban.com/news/detail-458074.html