图的结构比较复杂,任何两个节点之间都可能有关系。
图的存储分为顺序存储和链式存储。
顺序存储包括邻接矩阵和边集数组,
链式存储包括邻接表、链式前向星、十字链表和邻接多重表。
图的存储 —— 邻接矩阵
邻接矩阵通常采用一个一维数组存储图中节点的信息,采用一个二维数组存储图中节点之间的邻接关系。
【邻接矩阵的表示方法】
无向图、有向图和网的邻接矩阵的表示方法如下所述。
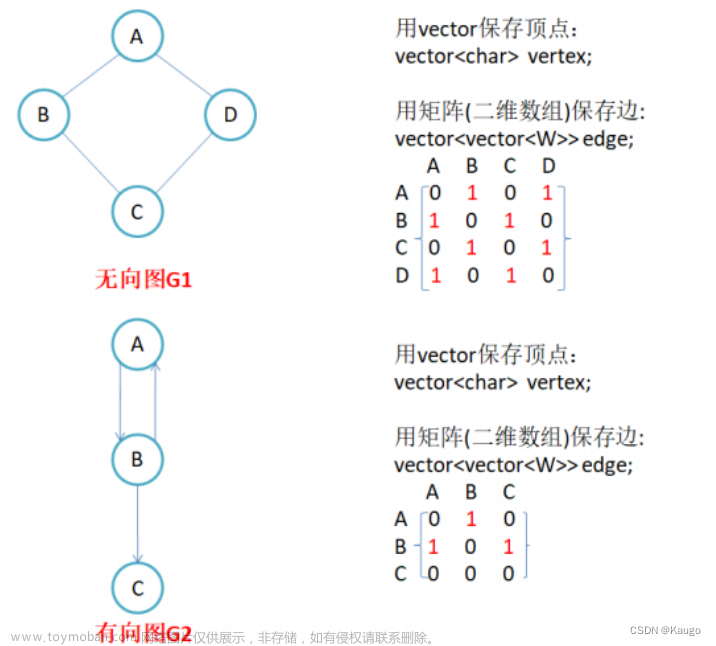
① 无向图的邻接矩阵
在无向图中,若从节点vi 到节点vj 有边,则邻接矩阵 M [ i ][ j ]= M [ j ][ i ]=1,否则 M [ i ][ j ]=0。

例如,一个无向图的节点信息和邻接矩阵如下图所示。

在该无向图中,从节点a 到节点b 有边,从节点b 到节点a 也有边,节点a 、b 在一维数组中的存储位置分别为0、1,则 M [ 0 ][ 1 ]= M [ 1 ][ 0 ]=1。

无向图的邻接矩阵的特点如下:
- 无向图的邻接矩阵是对称矩阵,并且是唯一的。
- 第i 行或第i 列非零元素的个数正好是第i 个节点的度。上图中的邻接矩阵,第3列非零元素的个数为2,说明第3个节点c 的度为2。
② 有向图的邻接矩阵
在有向图中,若从节点vi 到节点vj 有边,则邻接矩阵 M [ i ][ j ]=1,否则 M [ i ][ j ]=0。

以尖括号<vi ,vj >表示的是有序对,以圆括号(vi ,vj )表示的是无序对
例如,一个有向图的节点信息和邻接矩阵如下图所示。

在该有向图中,从节点a 到节点b 有边,节点a 、b 在一维数组中的存储位置分别为0、1,因此 M [ 0 ][ 1 ]=1。有向图中的边是有向边,从节点a 到节点b有边,从节点b 到节点a 不一定有边,因此有向图的邻接矩阵不一定是对称的。

有向图的邻接矩阵的特点如下:
- 有向图的邻接矩阵不一定是对称的。
- 第i 行非零元素的个数正好是第i 个节点的出度,第i 列非零元素的个数正好是第i 个节点的入度。上图中的邻接矩阵,第3行非零元素的个数为2,第3列非零元素的个数也为2,说明第3个节点c 的出度和入度均为2。
③ 网的邻接矩阵
网是带权图,需要存储边的权值,则邻接矩阵表示为

其中,wij 表示边上的权值,∞表示无穷大。当i =j 时,wii 也可被设置为0。
例如,一个网的节点信息和邻接矩阵如下图所示。

在该网中,从节点a 到节点b 有边,且该边的权值为2,节点a 、b 在一维数组中的存储位置分别为0、1,因此 M [ 0 ][ 1 ]=2。从节点b 到节点a 没有边,因此 M [ 1 ][ 0 ]=∞。

【邻接矩阵的数据结构定义】
首先定义邻接矩阵的数据结构,如下图所示。

#define MaxVnum 100 //节点数的最大值
typedef char VexType; //节点的数据类型,根据需要定义
typedef int EdgeType; //边上权值的数据类型,若为不带权值的图,则为0或1
【邻接矩阵的存储方法】
[算法步骤]
- 输入节点数和边数
- 依次输入节点信息,将其存储到节点数组Vex[]中;
- 初始化邻接矩阵,如果是图,则将其初始化为0;如果是网,则将其初始化为∞;
- 依次输入每条边依附的两个节点,如果是网,则还需要输入该边的权值。
- 如果是无向图,则输入a b ,查询节点a、b 在节点数组Vex[]中的存储下标i 、j ,令Edge[ i ][ j ]=Edge[ j ][ i ]=1
- 如果是无向网,则输入a b w ,查询节点a、b 在节点数组Vex[]中的存储下标i 、j ,令Edge[ i ][ j ]=Edge[ j ][ i ]=w 。
- 如果是有向网,则输入a b w ,查询节点a、b 在节点数组Vex[]中的存储下标i 、j ,令Edge[ i ][ j ]=w 。
[完美图解]
一个无向图如下图所示,其邻接矩阵的存储过程如下所述。

① 输入节点数和边数。
4 5
结果:G .vexnum=4、G .edgenum=5。
② 输入节点信息,将其存入节点信息数组。
a b c d
存储结果如下图所示。

③ 初始化邻接矩阵的值均为0,如下图所示。

④ 依次输入每条边依附的两个节点。
-
输入a b ,处理结果:在Vex[]数组中查找到节点a 、b 的下标分别为0、1,是无向图,因此令Edge[0][1]=Edge[1][0]=1,如下图所示。

-
输入a d ,处理结果:在Vex[]数组中查找到节点a 、d 的下标分别为0、3,是无向图,因此令Edge[0][3]= Edge[3][0]=1,如下图所示。

-
输入b c ,处理结果:在Vex[]数组中查找到节点b 、c 的下标分别为1、2,是无向图,因此令Edge[1][2]= Edge[2][1]=1,如下图所示

-
输入b d ,处理结果:在Vex[]数组中查找到节点b 、d 的下标分别为1、3,是无向图,因此令Edge[1][3]= Edge[3][1]=1,如下图所示

-
输入c d ,处理结果:在Vex[]数组中查找到节点c 、d 的下标分别为2、3,是无向图,因此令Edge[2][3]= Edge[3][2]=1,如下图所示

在实际应用中,也可以先输入节点信息并将其存入数组Vex[]。在输入边时直接输入节点的存储下标序号,这样可以节省查询节点下标所需的时间,从而提高效率。
[算法实现代码]
void CreateAMGragh(AMGragh &G){
int i , j ;
VexType u , v;
cout << "请输入节点数:" << endl;
cin >> G.vexnum;
cout << "请输入边数:" << endl;
cin >> G.edgenum;
cout << "请输入节点信息:" << endl;
for(int i = 0 ; i < G.vexnum ; i ++){ //输入节点信息,将其存入节点信息数组
cin >> G.Vex[i];
}
for(int i = 0 ; i < G.vexnum ; i++){ //初始化邻接矩阵的所有值为0,如果是网,则初始化其邻接矩阵为无穷大
for(int j = 0; j < G.vexnum ; j ++){
G.Edge[i][j] = 0;
}
}
cout << "请输入每条边依附的两个节点:" << endl;
while(G.edgenum --){
cin >> u >> v;
i = locatevex(G , u); //查找节点u 的存储下标
j = locatevex(G , v); //查找节点v 的存储下标
if(i != -1 && j != -1){
G.Edge[i][j] = G.Edge[j][i] = 1; //将邻接矩阵设置为1
}
}
}
【邻接矩阵的优缺点】
优点:
- 快速判断在两节点之间是否有边。在图中,Edge[i ][j ]=1,表示有边;Edge[i ][j ]=0,表示无边。在网中,Edge[i ][j ]=∞,表示无边,否则表示有边。时间复杂度为O (1)。
- 方便计算各节点的度。在无向图中,邻接矩阵第i 行元素之和就是节点i 的度;在有向图中,第i 行元素之和就是节点i 的出度,第i列元素之和就是节点i 的入度。时间复杂度为O (n )。
缺点:文章来源:https://www.toymoban.com/news/detail-458686.html
- 不便于增删节点。增删节点时,需要改变邻接矩阵的大小,效率较低。
- 不便于访问所有邻接点。访问第i 个节点的所有邻接点时,需要访问第i 行的所有元素,时间复杂度为O (n )。访问所有节点的邻接点,时间复杂度为O (n^2 )。
- 空间复杂度高,为O (n^2 )。
在实际应用中,如果在一个程序中只用到一个图,就可以用一个二维数组表示邻接矩阵,直接输入节点的下标,省去节点信息查询步骤。有时如果图无变化,则为了方便,可以省去输入操作,直接在程序头部定义邻接矩阵。
例如,可以直接定义图的邻接矩阵如下:文章来源地址https://www.toymoban.com/news/detail-458686.html
int M[m][n] = {{0,1,0,1} , {1,0,1,1} , {0,1,0,1} , {1,1,1,0}};
到了这里,关于图的存储 —— 邻接矩阵的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!