参数检验和非参数检验（结合SPSS分析）-Toy模板网

这篇具有很好参考价值的文章主要介绍了参数检验和非参数检验（结合SPSS分析）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

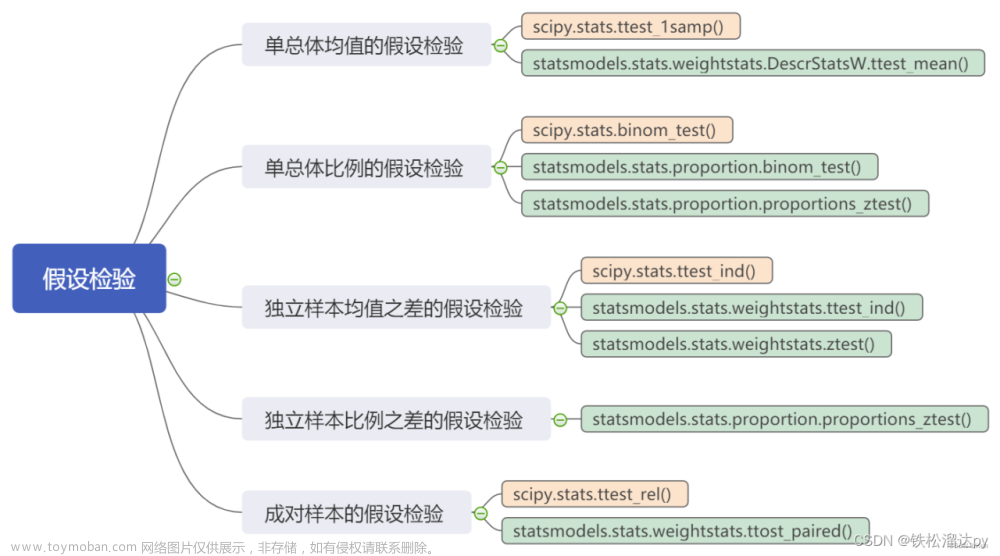
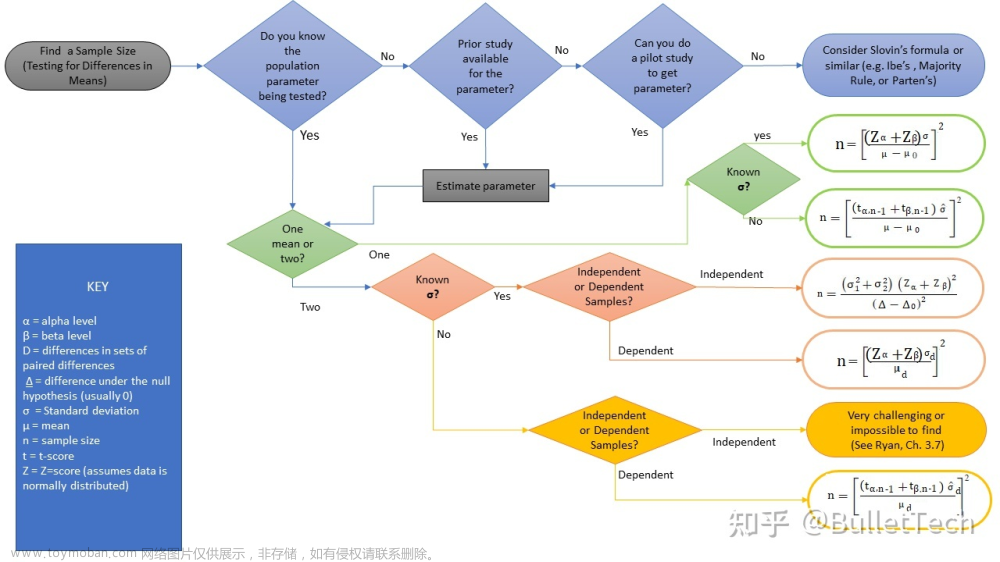
假设检验

概念：是一种根据样本数据来推断总体的分布或均值、方差等总体统计参数的方法。

根据样本来推断总体的原因：

总体数据不可能全部收集到。如：质量检测问题
收集到总体全部数据要耗费大量的人力和财力

假设检验包括：

参数检验
非参数检验

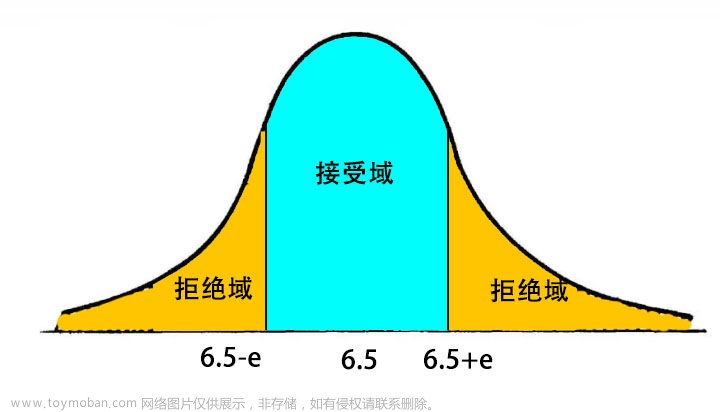
基本原理：利用小概率原理进行反证明。小概率事件在一次实验中不可能发生。

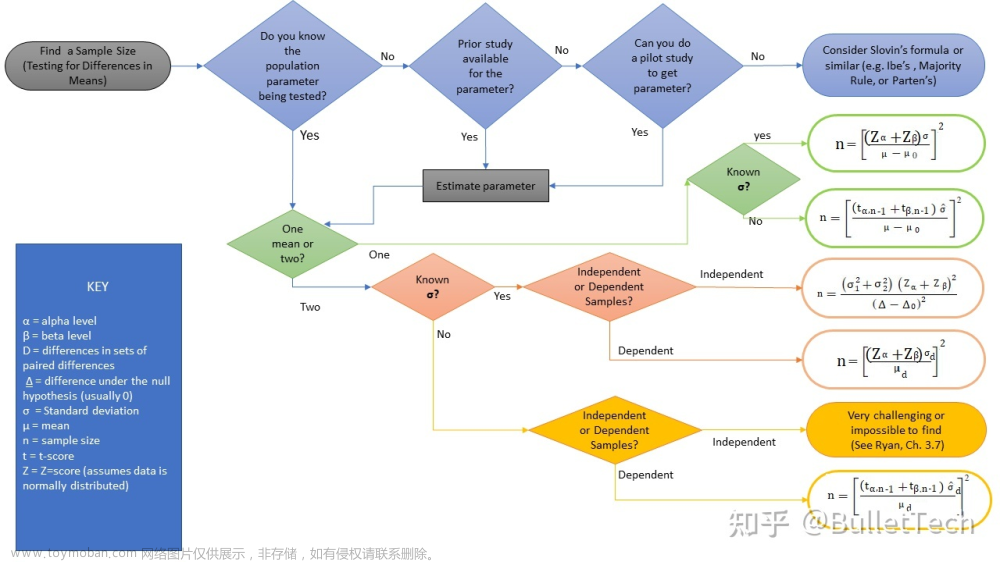
基本步骤：

根据检验的目标，对有待推断的总体参数或分布作一个零假设 $H_0$
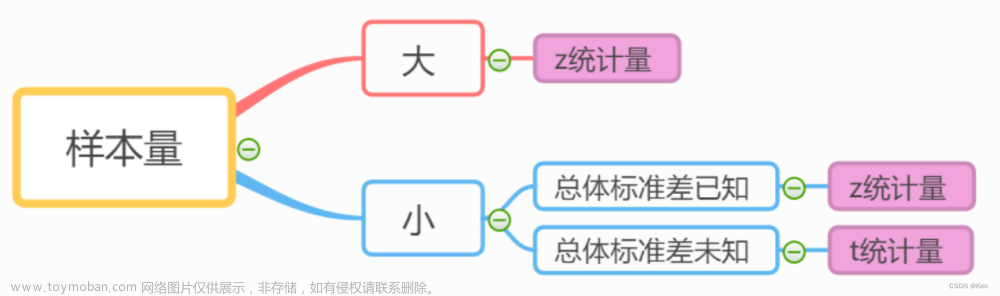
构造检验统计量,且该统计量服从某种已知分布.（卡方分布、t分布、F分布）
利用收集到的样本数据和基本假设计算检验统计量的值，并得到相应的相伴概率P值，即：检验统计量在某个特定的极端区域取值在 $H_0$ 成立时的概率.
给定显著性水平，如果概率P值小于用户给定的显著性水平 $\alpha$ (一般取0.05或0.01)，则拒绝零假设 $H_0$ 而接受备择假设。否则，不拒绝零假设 $H_0$ （类似一种反证法）。显著性水平指的是零假设正确却被错误拒绝的概率，一般取0.01或0.05，即零假设正确且正确接受的概率为99%或95%

参数检验

参数检验方法

平均值检验
单样本t检验
两独立样本t检验
两配对样本t检验

平均值检验

计算一个或多个自变量类别中因变量的子组平均值与相关的单变量统计，也可以通过比较两个样本的均值来判断两个总体的均值是否相等。零假设：两个样本的均值，没有显著差异。
实例
问题：判断男女生数学成绩的均值是否具有显著差异
操作：
点击>分析>比较平均值>平均值
参数检验和非参数检验（结合SPSS分析）
将性别拖到自变量列表，数学成绩拖到因变量列表。

点击选项按钮，勾选Anova表和eta、线性相关度检验
（如果自变量的个数少于3或者含有字符串，则无法进行线性相关度检验，因此此选项也可不必勾选）
参数检验和非参数检验（结合SPSS分析）
分析结果：

从ANOVA表中可以看出，显著性为0.36，大于0.05，说明男生和女生之间的数学成绩均值没有显著差异。

参数检验和非参数检验（结合SPSS分析）

从相关性测量表中看出Eta的平方为0.02

单样本t检验

$H_0$ : $u=u_0$ ,总体均值与检验值之间不存在显著差异.

构造检验统计量.从样本均值的分布出发,即:~ $N(u_0,\sigma^2/n)$ .于是：

总体方差未知时构造t统计量 $t=\frac{\overline D}{S/\sqrt{n}}$
$D=X- u_0$
t统计量服从n-1个自由度的t分布

计算t统计量和对应的相伴概率P(绝对值大于等于 $\alpha$ 的双侧概率)

结论: $P\leq\alpha$ ,则拒绝 $H_0$ ,认为总体均值与检验值之间有显著差异. $P>\alpha$ ,不能拒绝 $H_0$ ，认为总体均值与检验值之间没有显著差异

两独立样本t检验

含义: 在两个样本相互独立的前提下，检验两个样本的总体均值是否存在显著差异。零假设：两个样本数据的均值不存在显著差异。

例如：男生和女生的计算机平均成绩有显著差异吗？

要求:

两样本必须相互独立,即:抽取其中一批样本对抽取另一批样本没有任何影响.(如:北京周岁儿童与上海儿童的平均身高)
两总体服从正态分布

基本思路：

零假设 $H_0:u_1-u_2=0$ ,两总体均值无显著差异。
构造检验统计量.从两样本均值差的分布出发,即:~ $N(u_1-u_2,\sigma^2_{x_1-x_2} ).$ 于是两总体均方差未知时构造t统计量：
两总体均值差的抽样分布标准差：
- 方差相等：用合并方差
- 方差不等：
  - 计算t统计量和对应的相伴概率P (绝对值大于等于该值的双侧概率)

利用方差齐性（Levene）F检验确定两总体方差是否齐性。给定零假设 $H_0$ :两总体方差无显著差异。

首先计算每个个案与所属组均值之差并取绝对值.然后对其进行单因素方差分析.

如果已假设方差齐性行 F检验的 $P\leq\alpha$ ,则拒绝F检验的 $H_0$ ,认为方差不齐性;其次看未假设方差齐性（Unequal）行的t检验概率.如果 $\leq\alpha$ ,则拒绝t检验的 $H_0$ ,认为两总体均值有显著差异;如果 $>\alpha$ ,则不拒绝t检验的 $H_0$

如果F检验的 $>\alpha$ ,则不能拒绝F检验的 $H_0$ ,认为方差齐性;其次看已假设方差齐性（equal）行的t检验概率，t检验概率如果 $\leq\alpha$ ,则拒绝t检验的 $H_0$ ,认为两总体均值有显著差异;如果 $>\alpha$ ,则不拒绝t检验的 $H_0$
参数检验和非参数检验（结合SPSS分析）

实例：

问题：判断男女生数学成绩是否具有显著差异
SPSS操作：
点击>分析>比较平均值>独立样本T检验
参数检验和非参数检验（结合SPSS分析）
点击>定义组

分析结果：

在“列表方差相等性检验”框中，显著性为0.256，大于0.05，两组的总体方差齐性，则选择“已假设方差齐性”这一行的t检验结果。在“平均值相等性的t检验”中显著性（双尾）为0.346，大于0.05，说明两组数据的均值不存在显著差异。

配对样本t检验

含义: 根据配对样本对两总体均值是否有显著差异进行推断。零假设：两个配对样本数据的均值不存在显著差异。

例如：某种减肥茶是否有效

要求:

两样本数据必须两两配对,即:样本个数相同,个案顺序相同.如:减肥茶的效果、不同广告形式对销售额的影响.(控制了个案自身的影响)
两总体服从正态分布

非参数检验

卡方检验

目的：通过样本数据的分布来检验总体分布与期望分布或某一理论是否一致，零假设是样本的总体与期望没有显著差异。

基本思想：如果从一个随机变量X中随机抽取若干个样本均值，当这些样本落在 $X$ 的 $k$ 个互不相关的子集中的观察频数服从一个多项分布，当k趋于无穷时，这个多项分布服从卡方分布。

卡方检验的零假设是：两个变量之间没有显著差异。若两种检验（皮尔逊卡方、似然比）的渐进显著性水平（双向）都小于0.05，则拒绝零假设，若两种检验的双向显著性水平都大于0.05，则不能拒绝零假设。

即：若卡方的渐进显著性小于0.05，表明变量之间有显著差异，若卡方的渐进显著性大于0.05，表明变量之间没有显著差异。

基本方法:

根据已知总体的构成比计算出样本中各类别的期望频数，计算实际观察频数与期望频数的差距,即：计算卡方值 $\chi^2=\sum_{i=1}^{k}\frac{(\text{观测频数}-\text{预测频数})^2}{\text{预测频数}}$
卡方值越小,则实际频数和期望频数相差越小.如果P大于显著性水平 $\alpha$ ,不能拒绝 $H_0$ ,认为总体分布与已知分布无显著差异。