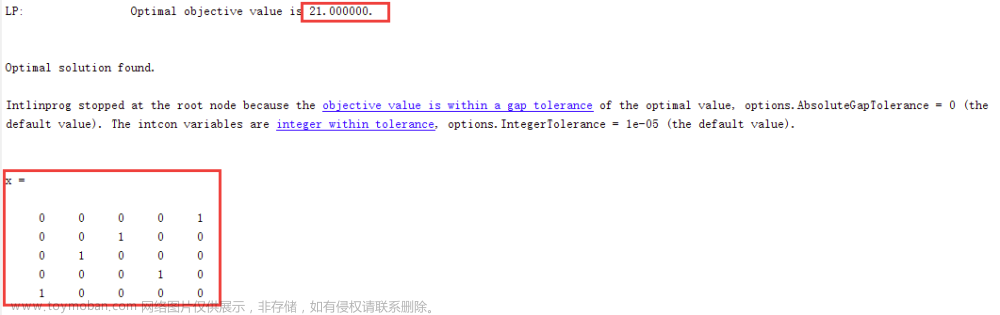
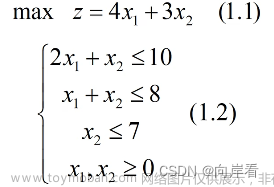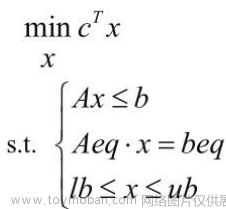线性规划
在人们的生产实践中,经常会遇到如何利用现有资源来安排生产,以取得最大经济
效益的问题。若目标函数及约束条件均为线性函数,则称为线性规划(Linear Programming 简记 LP)。
可行解:满足约束条件的解。
可行预:所有可行解构成的集合称为问题的可行域,记为R。

图解法:
图解法简单直观,有助于了解线性规划问题求解的基本原理。可得到如下结论:
(1)可行域 R 可能会出现多种情况。 R 可能是空集也可能是非空集合,当 R 非空
时,它必定是若干个半平面的交集。 R 既可能是有界区域,也可能是无界区域。
(2)在 R 非空时,线性规划既可以存在有限最优解,也可以不存在有限最优解(其
目标函数值无界)。
(3)若线性规划存在有限最优解,则必可找到具有最优目标函数值的可行域 R 的“顶点”。
整数规划
规划中的变量(部分或全部)限制为整数时,称为整数规划。若在线性规划模型中,变量限制为整数,则称为整数线性规划。目前所流行的求解整数规划的方法,往往只适用于整数线性规划。
如不加特殊说明,一般指整数线性规划。对于整数线性规划模型大致可分为两类:
- 变量全限制为整数时,称纯(完全)整数规划。
- 变量部分限制为整数的,称混合整数规划。
整数规划特点
- 原线性规划有最优解,当自变量限制为整数后,其整数规划解出现下述情况:
①原线性规划最优解全是整数,则整数规划最优解与线性规划最优解一致。
②整数规划无可行解。
③有可行解(当然就存在最优解),但最优解值变差。 - 整数规划最优解不能按照实数最优解简单取整而获得。

求解方法分类
- 分枝定界法—可求纯或混合整数线性规划。
- 割平面法—可求纯或混合整数线性规划。
- 隐枚举法—求解“0-1”整数规划:
①过滤隐枚举法;
②分枝隐枚举法。 - 匈牙利法—解决指派问题(“0-1”规划特殊情形)。
- 蒙特卡洛法—求解各种类型规划。
(1)分枝定界法
对有约束条件的最优化问题(其可行解为有限数)的所有可行解空间恰当地进行系统搜索,这就是分枝与定界内容。通常,把全部可行解空间反复地分割为越来越小的子集,称为分枝;并且对每个子集内的解集计算一个目标下界(对于最小值问题),这称为定界。在每次分枝后,凡是界限超出已知可行解集目标值的那些子集不再进一步分枝,这样,许多子集可不予考虑,这称剪枝。
设有最大化的整数规划问题 A ,与它相应的线性规划为问题 B ,从解问题 B 开始,若其最优解不符合 A 的整数条件,那么 B 的最优目标函数必是 A 的最优目标函数z* 的上界,记作 z- ;而 A 的任意可行解的目标函数值将是z* 的一个下界 z_ 。分枝定界法就是将 B 的可行域分成子区域的方法。逐步减小 z- 和增大 z_ ,最终求到z* 。
(2) 割平面法

(3) 隐枚举法(“0-1”整数规划)

(i) 先试探性求一个可行解,易看出(1,0,0)满足约束条件,故为一个可行解,且 z= 3 。
(ii) 因为是求极大值问题,故求最优解时,凡是目标值 z<3 的解不必检验是否满足约束条件即可删除,因它肯定不是最优解,于是应增加一个约束条件(目标值下界):
(iii) 改进过滤条件。
(iv) 由于对每个组合首先计算目标值以验证过滤条件,故应优先计算目标值 z 大的组合,这样可提前抬高过滤门槛,以减少计算量。
(4) 匈牙利法

匈牙利算法python代码:
import numpy as np
from scipy.optimize import linear_sum_assignment
cost = np.array([[3,5,8,4], [6,8,5,4], [2,5,8,5],[9,2,5,2]])
row_ind, col_ind = linear_sum_assignment(cost)
print(row_ind) # 开销矩阵对应的行索引
print(col_ind) # 对应行索引的最优指派的列索引
print(cost[row_ind, col_ind]) # 提取每个行索引的最优指派列索引所在的元素,形成数组
print(cost[row_ind, col_ind].sum()) # 数组求和
'''
输出:
[0 1 2 3]
[3 2 0 1]
[4 5 2 2]
13
'''
(5) 蒙特卡洛法(随机取样法)
是指使用随机数(或更常见的伪随机数)来解决很多计算问题的方法。
尽管整数规划由于限制变量为整数而增加了难度;然而又由于整数解是有限个,于是为枚举法提供了方便。当然,当自变量维数很大和取值范围很宽情况下,企图用显枚举法(即穷举法)计算出最优值是不现实的,但是应用概率理论可以证明,在一定的计算量的情况下,完全可以得出一个满意解。
指派问题的计算机求解
整数规划问题的求解可以使用 Lingo 等专用软件。对于一般的整数规划问题,无法
直接利用 Matlab 的函数,必须利用 Matlab 编程实现分枝定界解法和割平面解法。但对
于指派问题等 1 0− 整数规划问题,可以直接利用 Matlab 的函数 bintprog 进行求解。
非线性规划
如果目标函数或约束条件中包含非线性函数,就称这种规划问题为非线性规划问
题。
线性规划与非线性规划的区别:
如果线性规划的最优解存在,其最优解只能在其可行域的边界上达到(特别是可行
域的顶点上达到);而非线性规划的最优解(如果最优解存在)则可能在其可行域的任意一点达到。 文章来源:https://www.toymoban.com/news/detail-458766.html
文章来源:https://www.toymoban.com/news/detail-458766.html
- FUN是用M文件定义的函数f(x)
- x0是x的初始值
- A,B,Aeq,Beq定义了线性约束,若没有则为空
- LB和UB是变量x的下界和上界
- NONLCON是用M文件定义的非线性向量函数C(x),Ceq(x)
- OPTIONS定义了优化参数,可以使用Matlab 缺省的参数设置。



二次规划
若某非线性规划的目标函数为自变量 x 的二次函数,约束条件又全是线性的,就称
这种规划为二次规划。
返回值 X 是决策向量 x 的值,返回值 FVAL 是目标函数在 x 处的值。文章来源地址https://www.toymoban.com/news/detail-458766.html
到了这里,关于数学建模整理-线性规划、整数规划、非线性规划的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!