【数据结构】广度优先遍历（BFS）模板及其讲解-Toy模板网

这篇具有很好参考价值的文章主要介绍了【数据结构】广度优先遍历（BFS）模板及其讲解。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

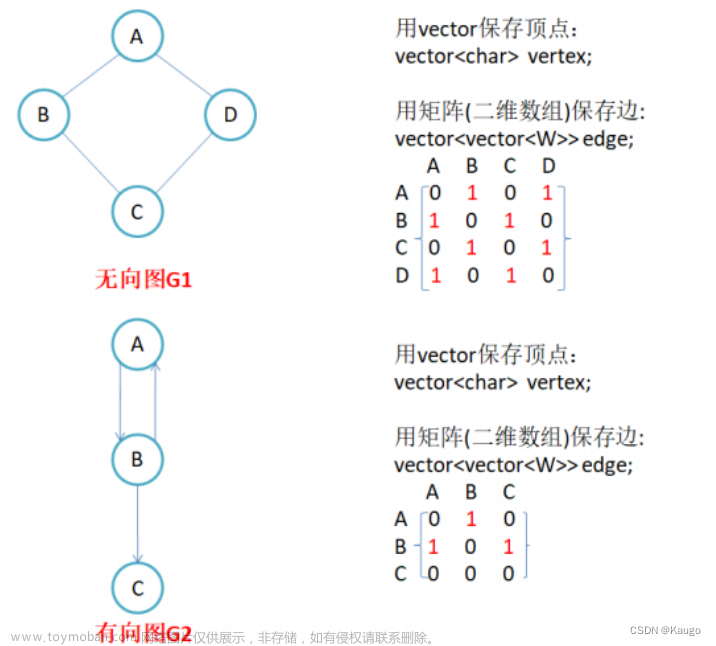
🎊专栏【数据结构】

🍔喜欢的诗句：更喜岷山千里雪三军过后尽开颜。

🎆音乐分享【勋章】

大一同学小吉，欢迎并且感谢大家指出我的问题🥰

文章来源地址https://www.toymoban.com/news/detail-458903.html

🎁定义

🎁遍历方法

🎁根据题目来理解BFS

🏳️‍🌈走迷宫

🏳️‍🌈思路

🏳️‍🌈代码（BFS模板）

🏳️‍🌈分析

🎁定义

BFS 全称是 Breadth-First-Search，即广度优先搜索。它是一种图遍历算法，在搜索时先访问起始顶点的所有邻居顶点，然后再依次访问这些邻居顶点的邻居顶点，直到遍历完整个图。这种算法可以用来寻找两个节点之间的最短路径，也可以用于树的遍历等其他场景。

BFS 通常使用队列来实现，从起始顶点开始，将其加入队列中，然后访问它的邻居顶点，并将其加入队列尾部。接着将队列头部的顶点出队并访问其邻居顶点，将未访问的邻居顶点加入队列中，直到队列为空为止。

BFS 算法在运行时，由于是逐层遍历，因此每一层的节点都会被访问，遍历到的第一个目标节点所在的层数也就是最短距离，因此 BFS 算法可以用来求解无权图的最短路径问题。

🎁遍历方法

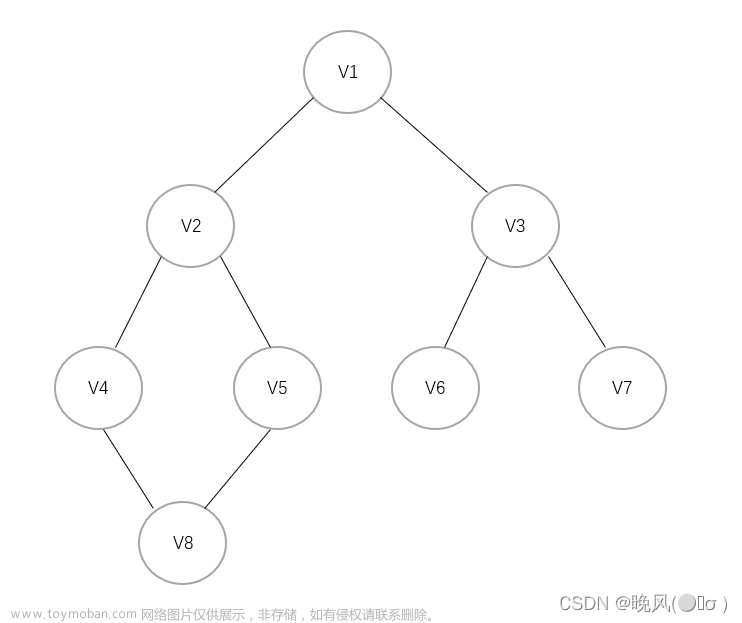
如下图所示

【数据结构】广度优先遍历（BFS）模板及其讲解

由于是逐层遍历，那么遍历顺序是 1 -> 2 -> 3 -> 4 -> 5 - > 6 -> 7 - > 8

🎁根据题目来理解BFS

🏳️‍🌈走迷宫

给定一个n*m的二维整数数组，用来表示一个迷宫，数组中只包含0或1，其中0表示可以走的路，1表示不可通过的墙壁。

最初，有一个人位于左上角(1, 1)处，已知该人每次可以向上、下、左、右任意一个方向移动一个位置。

请问，该人从左上角移动至右下角(n, m)处，至少需要移动多少次。

数据保证(1, 1)处和(n, m)处的数字为0，且一定至少存在一条通路。

输入格式

第一行包含两个整数n和m。

接下来n行，每行包含m个整数（0或1），表示完整的二维数组迷宫。

输出格式

输出一个整数，表示从左上角移动至右下角的最少移动次数。

数据范围

1≤n,m≤100

输入样例：
5 5
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0
输出样例：
8

🏳️‍🌈思路

从起点开始，往前走第一步，记录下所有第一步能走到的点，然后从所第一步能走到的点开始，往前走第二步，记录下所有第二步能走到的点，重复下去，直到走到终点。输出步数即可。

🏳️‍🌈代码（BFS模板）

#include <cstring>   // 处理内存块的头文件
#include <iostream>  // 标准输入输出头文件
#include <algorithm> // STL 常用算法头文件
#include <queue>     // 队列头文件

using namespace std;  // 命名空间

typedef pair<int, int> PII;  // 定义 pair 类型

const int N = 110;  // 设定二维数组的大小

int n, m;           // n 和 m 分别代表二维数组的行和列
int g[N][N], d[N][N];  // g 表示从输入中读取的二维数组信息，d 用来记录遍历每个点的距离

int bfs()  // BFS 算法主函数
{
    queue<PII> q;  // 定义一个队列，队列中的元素是 pair 类型的变量

    memset(d, -1, sizeof d);  // 初始化距离数组 d 数组的值都设置为 -1，表示还未遍历到
    d[0][0] = 0;  // 起点格子的距离设置为 0
    q.push({0, 0});  // 将起点的坐标加入队列中

    int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};  // 定义上右下左四个方向的移动距离

    while (q.size())  // 队列不为空
    {
        auto t = q.front();  // 取出队首元素，并标记当前这个点已经访问过了
        q.pop();

        for (int i = 0; i < 4; i ++ )  // 尝试四个方向的移动
        {
            int x = t.first + dx[i], y = t.second + dy[i];  // 计算出移动后的点的坐标

            if (x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1)  // 如果移动后的点满足条件（没有越界、不是障碍、且未遍历到）
            {
                d[x][y] = d[t.first][t.second] + 1;  // 更新移动后的点的距离
                q.push({x, y});  // 将新的点加入队列
            }
        }
    }

    return d[n - 1][m - 1];  // 返回终点的距离，即最短路径长度
}

int main()  // 主函数
{
    cin >> n >> m;  // 读入二位数组的行和列数
    for (int i = 0; i < n; i ++ )  // 读入二维数组的每一个元素
        for (int j = 0; j < m; j ++ )
            cin >> g[i][j];

    cout << bfs() << endl;  // 调用 BFS 算法函数，输出最少需要多少步才能从起点走到终点

    return 0;  // 返回运行成功标志
}

🏳️‍🌈分析

~用 g 存储地图，f存储起点到其他各个点的距离。
~从起点开始广度优先遍历地图。
~当地图遍历完，就求出了起点到各个点的距离，输出d[n][m]即可。

【数据结构】广度优先遍历（BFS）模板及其讲解

while (q.size()) // 队列不为空
{
auto t = q.front(); // 取出队首元素，并标记当前这个点已经访问过了
q.pop();

for (int i = 0; i < 4; i ++ ) // 尝试四个方向的移动
{
int x = t.first + dx[i], y = t.second + dy[i]; // 计算出移动后的点的坐标

if (x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1) // 如果移动后的点满足条件（没有越界、不是障碍、且未遍历到）
{
d[x][y] = d[t.first][t.second] + 1; // 更新移动后的点的距离
q.push({x, y}); // 将新的点加入队列
}
}
}

上面这一段代码就是来寻找下一步要走的路，尝试四个方向的移动，int x = t.first + dx[i], y = t.second + dy[i]; 计算出移动后的点的坐标，判断4个方向是否满足移动条件【if (x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1) 没有越界、不是障碍、且未遍历到）】，如果找到了，就 d[x][y] = d[t.first][t.second] + 1；更新移动后的点的距离（距离+1），并且 q.push({x, y}); 将新的点加入队列，标记这一点，表示这个点已经访问过了