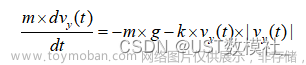2023五一数学建模竞赛C题思路+数据+论文-Toy模板网

这篇具有很好参考价值的文章主要介绍了2023五一数学建模竞赛C题思路+数据+论文。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

问题1：现在有一间长4米、宽3米、高3米的单层平顶单体建筑，墙体为砖混结构，厚度30厘米(热导系数0.3W/㎡·K)，屋顶钢筋混凝土浇筑，厚度30厘米(热导系数0.2W/㎡·K)，门窗总面积5平方(热导系数1.6W/㎡·K)，地面为混凝土 (热导系数0.25W/㎡·K)。该建筑物所处地理位置一年(按365天计算)的月平均温度(单位：摄氏度）见下表。

问题一：假设该建筑物内温度需要一直保持在18-26度，在温度不适宜的时候要通过电来调节温度，消耗一度电相当于0.28千克碳排放。请计算该建筑物通过空调(假设空调制热性能系数COP为3.5，制冷性能系数EER为2.7)调节温度的年碳排放量。(尽量使用本题所给条件计算碳排放，不考虑其他损耗)

为了计算建筑物通过空调调节温度的年碳排放量，我们需要先计算每个月的供暖和制冷需求。建筑物的热损失或热增加与墙体、屋顶、门窗和地面的热传导系数以及室内外温差有关。我们可以使用以下公式计算热损失或热增加：

热损失或热增加 = 表面积 × 热导系数 × 温差

我们要先计算墙体、屋顶、门窗和地面的表面积，墙体表面积 = (4m × 3m × 2 + 3m × 3m × 2)，屋顶表面积 = 4m × 3m，门窗总面积已给出为5平方米，地面表面积 = 4m × 3m。

室内温度需要保持在18-26度，可以根据每个月的平均温度计算室内外温差。例如，1月份的室内外温差为：18 - (-1) = 19度（供暖），其他月份类似计算。

使用公式计算每个月的热损失或热增加，然后将每个部分的热损失或热增加相加。并且根据空调的COP和EER，将每个月的热损失或热增加转换为电能需求。例如，1月份的电能需求为：热损失 / COP，其他月份类似计算。将每个月的电能需求相加得到年度总电能需求，然后乘以每度电产生的碳排放（0.28千克/度电）得到年碳排放量。

问题2：在居住建筑的整个生命周期 (建造、运行、拆除)中，影响碳排放的因素有很多，如建筑设计标准、气候、建材生产运输、地区差异、建造拆除能耗、装修风格、使用能耗、建筑类型等。请查找、分析资料，建立数学模型，找出与上述因素相关度大且易于量化的指标，基于这些指标对居住建筑整个生命周期的碳排放进行综合评价。

为了对居住建筑的整个生命周期的碳排放进行综合评价，我们可以建立一个线性加权模型，该模型将各个指标的相关度与其易于量化程度进行综合考虑。首先需要确定各指标的权重，然后将各指标的值乘以相应的权重求和以得到综合评价值。确定与碳排放相关度大且易于量化的指标：根据您提供的因素，我们可以考虑以下指标：

建筑设计标准：例如，建筑节能等级

气候：例如，年平均气温、年降水量

建筑材料生产运输：例如，每平方米建筑所需材料的碳排放量

建筑能耗：例如，每平方米每年的供暖和制冷能耗

建筑类型：例如，单层、多层或高层建筑

根据各指标对碳排放的影响程度和易于量化程度分配权重。例如，建筑能耗可能对碳排放的影响程度较高，因此可以分配较大的权重。权重之和应为1。将各指标的值乘以相应的权重求和，得到综合评价值。

综合评价值 = w1 * 建筑设计标准 + w2 * 气候 + w3 * 建筑材料生产运输 + w4 * 建筑能耗 + w5 * 建筑类型

其中，w1、w2、w3、w4、w5分别为各指标的权重。

这种线性加权模型简单易懂，可以为决策者提供直观的评价结果。但是各指标之间可能存在相互影响，而这种影响在线性加权模型中无法体现。

问题3：在问题2的基础上，分别考虑建筑生命周期三个阶段的碳排放问题，查找相关资料，建立数学模型，对2021年江苏省13个地级市的居住建筑碳排放进行综合评价，并对所建评价模型的有效性进行验证。

在问题2的基础上，我们可以将居住建筑的碳排放划分为三个阶段：建造、运行、拆除。首先，我们需要针对每个阶段确定相关度大且易于量化的指标。然后，为每个阶段的指标分配权重。最后，将各阶段指标的值乘以相应的权重求和，得到综合评价值。