相关信息
(1)建模思路
【2023 年第十三届 MathorCup 高校数学建模挑战赛】A 题 量子计算机在信用评分卡组合优化中的应用 详细建模过程解析及代码实现
【2023 年第十三届 MathorCup 高校数学建模挑战赛】 B 题 城市轨道交通列车时刻表优化问题 详细建模方案及代码实现
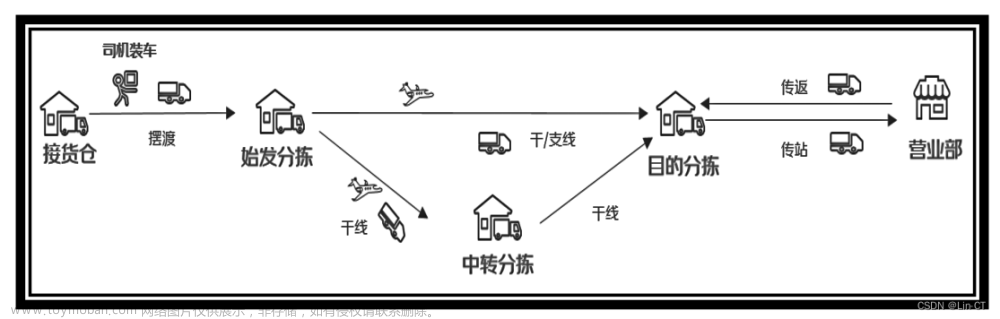
【2023 年第十三届 MathorCup 高校数学建模挑战赛】C 题 电商物流网络包裹应急调运与结构优化问题 建模方案及代码实现
(2)完整论文
【2023 年第十三届 MathorCup 高校数学建模挑战赛】A 题 量子计算机在信用评分卡组合优化中的应用 42页论文及代码
【2023 年第十三届 MathorCup 高校数学建模挑战赛】 B 题 城市轨道交通列车时刻表优化问题 42页论文及代码
【2023 年第十三届 MathorCup 高校数学建模挑战赛】C 题 电商物流网络包裹应急调运与结构优化问题 赛后总结之31页论文及代码
[【2023 年第十三届 MathorCup 高校数学建模挑战赛】D 题 航空安全风险分析和飞行技术评估问题 27页论文及代码](
【2023 年第十三届 MathorCup 高校数学建模挑战赛】 B 题 城市轨道交通列车时刻表优化问题 42页论文及代码
相关链接
【2023 年第十三届 MathorCup 高校数学建模挑战赛】 B 题 城市轨道交通列车时刻表优化问题 详细建模方案及代码实现
1 题目
列车时刻表优化问题是轨道交通领域行车组织方式的经典问题之一。 列车时刻表规定了列车在每个车站的到达和出发(或通过)时刻,其在实 际运用过程中,通常用列车运行图来表示。图 1 为某一运行图的示例,图中每一条线表示一趟列车,横轴表示车站,纵轴表示时间,每一条线反映 了一趟列车在不同时刻所处的相对位置,也称为运行线。比如,图中红色 运行线表示,列车于 9:02 分从 D 站出发,于 9:05 分到达 C 站,停留 1 分钟后出发,于 9:09 分到达 B 站,停留 1 分钟后出发,于 10:03 分到达A 站。

图 1: 列车运行图示意图
实际运营中,在铺画列车运行图之前,首先得先确定列车开行方案, 列车开行方案包括列车编组方案、列车停站方案和列车交路计划三部分。列车编组方案规定了列车的车型和编组数量(即列车的节数),在本问题中采用统一的车型和编组数量。列车停站方案是规定列车在哪些站点停站的方案,在本问题中均采用 站站停的停站方案(即列车在每个经过的车站都会停车)。列车交路计划是指列车在规定的运行线路上往返运行的方式,即规定 了列车在哪些站点之间运行以及开行的数量。大小交路模式是城轨运营中 常用的交路模式,是指城市轨道交通运行线路的长短区间。通俗讲,大交 路是指列车跑完全程,小交路是指将全程中的某两个站作为临时起点或终 点来跑,需要注意的是,只有具有折返能力的车站(能让列车调头的车站) 才能作为交路的起点或终点。图 2 为某大小交路方案示意图,表示以 A 站为起点的,D 站为终点大交路区间开行 10 对列车,以 A 站为起点,C 站为终点小交路区间开行 5 对列车。
在大小交路方案中,大小交路列车开行列数通常为1:n 或n:1 两种模式, 即每开行 n 列大(小)交路列车后,开行一列小(大)交路列车,并且小交路所经过的车站数量需有一定限制:小交路区间过短会导致列车的折返频繁,使运营成本增加;小交路区间过长则无法体现大小交路运营模式的作用。
图 2: 大小交路示意图
在大小交路的运营模式下,乘客通常会被分为 6 种类型,如图 3 所示, 其中s1 − sn为大交路区间,𝑠𝑎 − 𝑠𝑏为小交路区间。
第Ⅰ,Ⅱ,Ⅲ类乘客起点均位于[s1, sa],终点无论位于哪个区间,乘客都只能乘坐大交路列车。第Ⅳ,Ⅴ类乘客起点均位于[𝑠𝑎, 𝑠𝑏]。其中第Ⅳ类乘客终点位于[𝑠𝑎, 𝑠𝑏], 乘客既可乘坐大交路列车,也可乘坐小交路列车;第Ⅴ类乘客终点位于[𝑠𝑏,𝑠𝑛],乘客可以乘坐小交路列车之后到𝑠𝑏进行换乘,也可直接乘坐大交路列车。第Ⅵ类乘客起点位于[𝑠𝑏, 𝑠𝑛],终点位于[𝑠𝑏, 𝑠𝑛],乘客只能乘坐大交路列车。

图 3 :乘客类型分类示意图
在列车开行方案的制定中,需要以最小的企业运营成本和最大的服务 水平(乘客在车时间和乘客等待时间)来满足客流的需求,企业的运营成本包 括固定成本(所需车辆的数量)和变动成本(列车总走行公里)两部分组 成。受到车站通过能力的制约和服务水平的要求,在一定时间内,列车的 发车数量也有一定的限制。在制定好列车开行方案后,可根据该方案同样以企业运营成本最小化 和服务水平最大化为目标铺画列车运行图,即确定每趟列车的出发和到达的具体时刻。现有的列车时刻表通常为等间隔的平行运行图,即发车间隔(如每 5 分钟开行一趟列车)和在同一站点的停站时间相等。发车间隔的长短会有一定的限制:发车间隔过短,则会影响列车运行的安全;发车间 隔过长,则会增长乘客的平均等待时间,从而影响服务水平。同样地,停 站时间也需受到一定限制,一般来说列车在车站的停站时间正比于在该站 上、下车的乘客数量。另外,需要注意的是,两列车在同一区间追踪运行 时,需保留一定的安全间隔(追踪间隔时间)。
采用大小交路运营模式的列车运行图,大交路列车和小交路列车一般 会交替开行,比如当大交路列车与小交路列车的比例为 2:1 时,则会以每3 列车为一个组合(前 2 列车为大交路列车,第三列车为小交路列车)滚动发车。
在下列问题中,只需制定单向的列车时刻表即可。
问题一:在满足客流需求的条件下,以企业运营成本最小化和服务水平最大化为目标,制定列车开行方案。即确定大交路区间列车的开行数量, 小交路的运行区间以及开行数量。(输出格式详见附件 6)
问题二:在问题一制定的列车开行方案下,同样以企业运营成本最小化和服务水平最大化且尽量满足客流需求为目标,制定等间隔的平行运行 图。(输出格式详见附件 7,并将附件 7 单独上传到竞赛系统中)
问题三:对于降低企业运营成本和提高服务水平,你们团队有哪些好的方法或建议?基于客流和车站数据,提供相应的量化分析支持。
名词解释:
乘客在车时间:即乘客从上车到下车所经过的时间,包括列车区间运行时间和停站时间两部分组成。
乘客等待时间:即为乘客在站台候车的等待时间。
断面客流:在单位时间内,沿同一方向通过线路某断面的乘客数量。
如何根据断面客流计算各个断面所需的列车数量:开行数量= ⌈断面客流数/列车定员⌉(向上取整)。
OD 客流:在单位时间内,起始站点到终止站点的乘客人数。
关于等间隔的补充解释:当采用大小交路运营模式时,等间隔为在大交路与小交路重合的区间的发车间隔相等。
输入输出数据:
所给数据为某实际轨道交通线路的真实数据,沿途共有 30 座车站,客流数据的时段为 7:00 - 8:00。数据详见附件。
附件 1:车站数据.xlsx
附件 2:区间运行时间.xlsx 附件 3:OD 客流数据.xlsx 附件 4:断面客流数据.xlsx 附件 5:其他数据.xlsx
附件 6:问题一输出示例.xlsx
附件 7:问题二输出示例.xlsx
2 论文介绍
城市轨道交通是大城市公共交通的重要组成部分,随着城市规模的不断扩大和人口的增加,轨道交通的客流量也在不断增加。因此,如何优化城市轨道交通列车时刻表,提高列车的运营效率和客运能力,已成为一个亟待解决的问题。
针对问题一,本文先通过查阅文献和关键指标转化将问题简化,主要采用**C++**代码实现,首先运用贪心算法达到企业运营成本最小化。后两次运用二分搜索法,第一次枚举小交路列车数量确定其数量区间,第二次枚举小交路列车运行长度,确定其运行列数。最后建立多约束受限,多主体协同下两个目标函数的多目标规划模型,数值计算优化调度列车开行方案。
针对问题二,基于模型一所建立模型由层次分析法得到各个站点的权值,来确定乘客人数高谷站点,及时满足乘客的需求使服务水平最大化。依据列车交替开行的运营模式,考虑时间安全间隔,得到列车发行的时刻表,制定等间隔的平行运行图。
针对问题三,要改变列车类型及编组数量,增加列车定员,提升列车最大载客量,从而减少列车数量,降低乘客候车时间,实现企业运营成本最小化和服务水平最大化目标,使得模型再次优化。
最后,对模型进行了优缺点分析,对模型进行改进策略并进行推广。
关键词:列车时刻优化表;贪心算法 ;二分搜索法 ;check 判断函数;多目标规划 ; 层次分析法

 文章来源:https://www.toymoban.com/news/detail-459257.html
文章来源:https://www.toymoban.com/news/detail-459257.html
3 获取方式
 文章来源地址https://www.toymoban.com/news/detail-459257.html
文章来源地址https://www.toymoban.com/news/detail-459257.html
到了这里,关于【2023 年第十三届 MathorCup 高校数学建模挑战赛】 B 题 城市轨道交通列车时刻表优化问题 42页论文及代码的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!