2021 年高教社杯全国大学生数学建模竞赛 E 题中药材的鉴别第一题-Toy模板网

这篇具有很好参考价值的文章主要介绍了2021 年高教社杯全国大学生数学建模竞赛 E 题中药材的鉴别第一题。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

1.数据预处理

1.1 数据基本信息探索

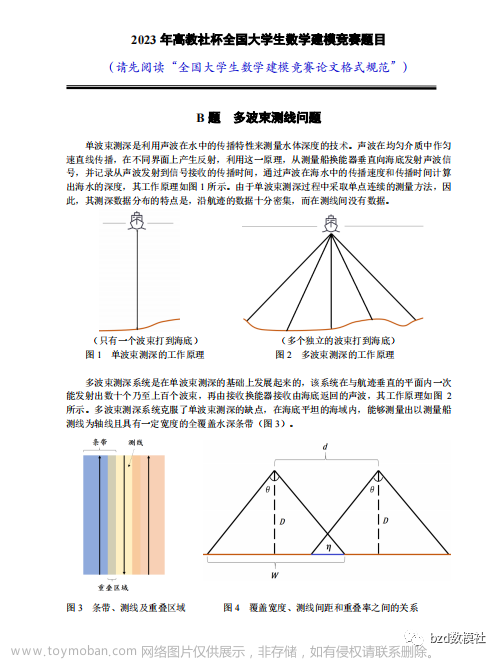
1.2 数据可视化

1.3 异常值处理

2. 数据特征值提取

2.1 数据标准化

2.2 PCA提取特征值

3. 数据聚类鉴别药材种类

3.1 肘部图确定K值

3.2 轮廓系数图确定K值

3.3 数据聚类

3.4 聚类结果可视化

4. 研究不同种类药材的特征和差异性

4.1 不同种类药材光谱数据均值曲线

4.2 不同种类药材光谱数据标准差曲线图

4.3 计算每类中药材光谱图的光谱信息散度SID

2021 年高教社杯全国大学生数学建模竞赛 E 题中药材的鉴别第一题

关注公众号获取完整代码文章来源地址https://www.toymoban.com/news/detail-459282.html

1.数据预处理

1.1 数据基本信息探索

根据附件 1 中几种药材的中红外光谱数据，研究不同种类药材的特征和差异性，并鉴别药材的种类。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = 'SimHei' # 设置中文显示
plt.rcParams['axes.unicode_minus'] = False

data = pd.read_excel('附件1.xlsx',index_col = 0) # index_col指定索引
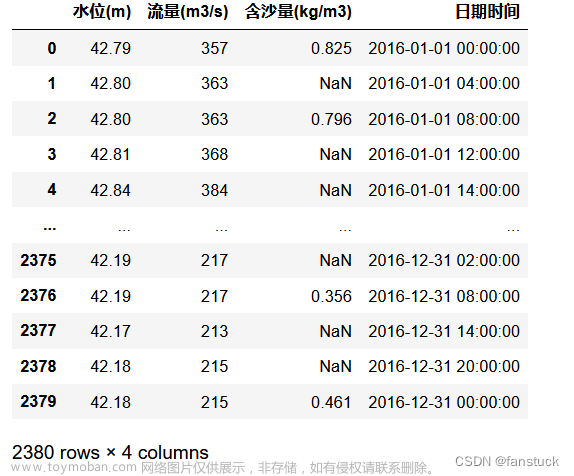
data.head()

data.shape # 数据维度

# (425, 3348)

data.info() # 数据基本信息

data.isnull().any().any() # 空值判断

# False

2021 年高教社杯全国大学生数学建模竞赛 E 题中药材的鉴别第一题

探索发现数据不存在缺失值情况

1.2 数据可视化

# 数据可视化
def func_1(x):
    plt.plot(#####)

def func_2(data):
    fontsize = 5
    plt.figure(figsize=(8, 6), dpi = 300)
    ########
    plt.yticks(fontsize = fontsize)
    plt.xlabel('波数(cm^-1)')
    plt.ylabel('吸光度(AU)')
    plt.grid(True) # 网格线设置
    data.agg(lambda x: func_1(x), axis = 1)
    plt.show()

func_2(data)

可视化结果显示存在三条光谱数据明显为离群数据，可能为异常值也可能为单独类

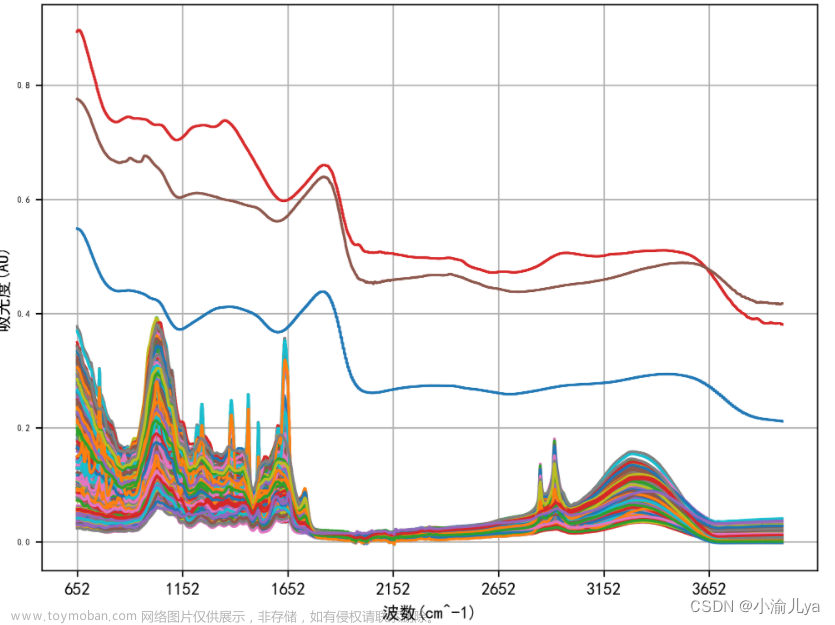
2021 年高教社杯全国大学生数学建模竞赛 E 题中药材的鉴别第一题

1.3 异常值处理

引入三倍西格玛法则检查数据是否存在异常值，并输出异常值索引，并删除异常值为接下来鉴别药材的种类做准备

#异常值检验3σ
def func_3(x):
    lower = x.mean()-3*x.std() 
    toplimit = x.mean()+3*x.std()
    return (x<lower)|(x>toplimit)

ycz = data.agg(lambda x:func_3(x))
ycz_index = data[(*******)].index
ycz_index

# Int64Index([64, 136, 201], dtype='int64', name='No')


data.drop(****,axis=0,inplace = True)


func_2(data)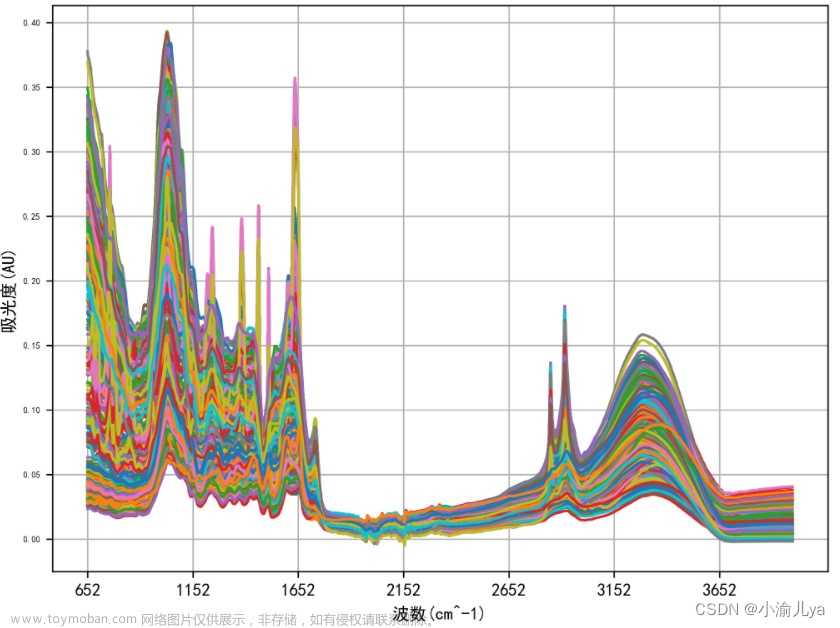

2021 年高教社杯全国大学生数学建模竞赛 E 题中药材的鉴别第一题

data.to_excel('data_ycl.xlsx')

2. 数据特征值提取

对数据提取特征值为接下来鉴别药材的种类做准备

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
plt.rcParams['font.sans-serif'] = 'SimHei' # 设置中文显示
plt.rcParams['axes.unicode_minus'] = False

data = pd.read_excel('data_ycl.xlsx', index_col = 0)

2.1 数据标准化

# 0-1标准化
arr_max = np.max(data)
arr_min = np.min(data)
data_bzh = (data-arr_min)/(arr_max-arr_min)
data_bzh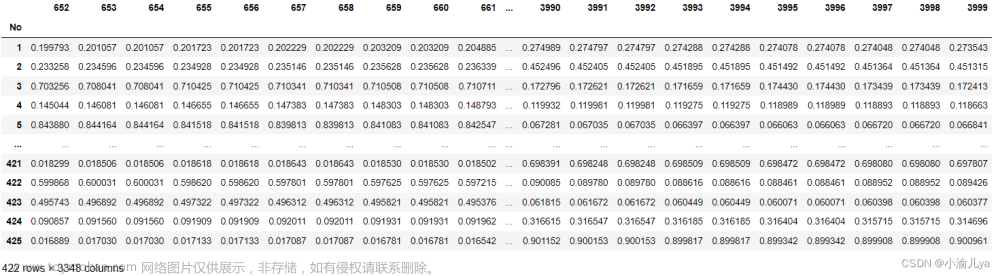

2021 年高教社杯全国大学生数学建模竞赛 E 题中药材的鉴别第一题

2.2 PCA提取特征值

采用主成分分析法提取特征值

pca = PCA()
pca.fit(data_bzh)
pca.explained_####### # 贡献率

lg = np.cumsum(#####) #累计贡献率

a = [0.59843097, 0.88309499, 0.93970633, 0.97403493, 0.9853352 ,0.98891337, 0.99174341]
plt.figure(figsize=(8, 6), dpi = 300)
plt.plot(a)
plt.title('前七个主成分累计贡献率')
plt.xlabel('主成分')
plt.ylabel('累计贡献率')
plt.grid(True)
plt.savefig('前七个主成分累计贡献率.png')
plt.show()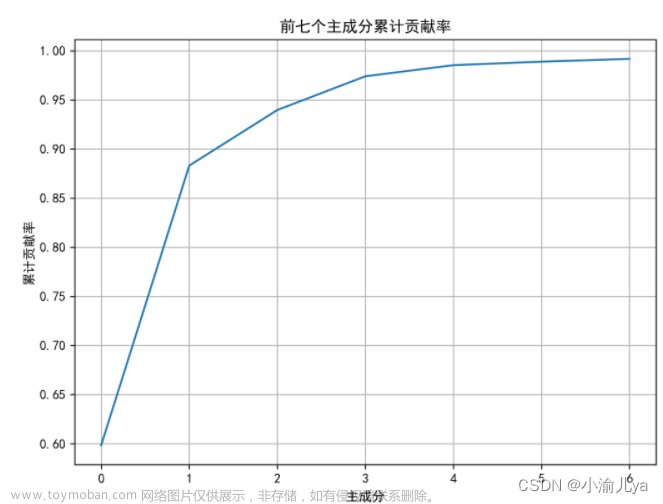

2021 年高教社杯全国大学生数学建模竞赛 E 题中药材的鉴别第一题

根据碎石图确定主成分

pca = PCA(3) # 选取累计贡献率大于90%的主成分（3个主成分）
pca.fit(data_bzh)
data_jw = pca.transform(data_bzh)
data_jw

3. 数据聚类鉴别药材种类

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from collections import Counter
from sklearn import metrics
from mpl_toolkits.mplot3d import Axes3D 
plt.rcParams['font.sans-serif'] = 'SimHei' # 设置中文显示
plt.rcParams['axes.unicode_minus'] = False

data = pd.read_excel('data_jw.xlsx',index_col = 0)

3.1 肘部图确定K值

SSE = []
for k in ####:
    ############
    km.fit(####)
    SSE.append(#####)
    
X = range(1, 11)
plt.figure(figsize=(8, 6), dpi = 300)
plt.xlabel('k')
plt.ylabel('SSE')
plt.title('肘部图')
plt.plot(X, SSE, 'o-')
plt.grid(True)
plt.savefig('肘部图.png')
plt.show()

利用肘部图，轮廓系数图确定k值

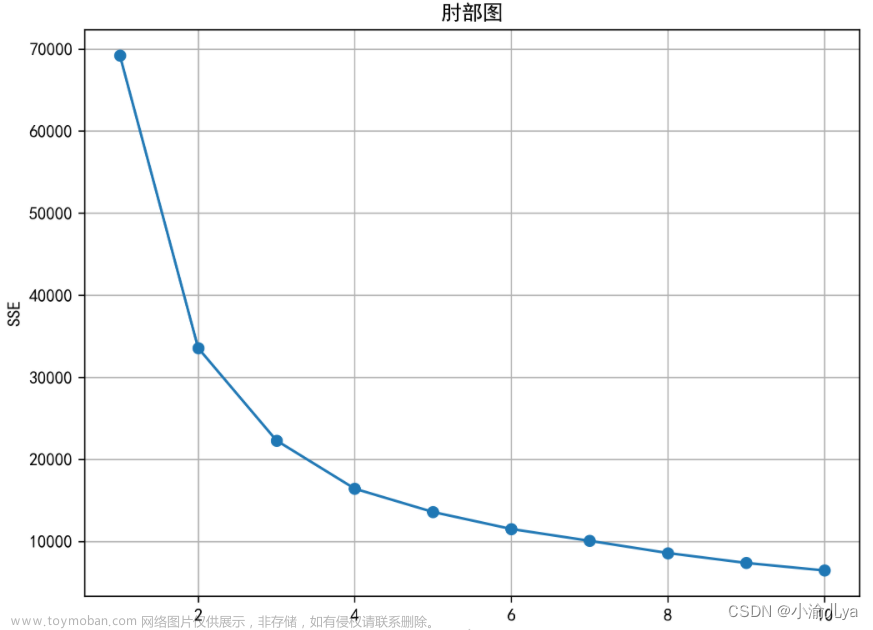
2021 年高教社杯全国大学生数学建模竞赛 E 题中药材的鉴别第一题

3.2 轮廓系数图确定K值

scores = []
for k in #####:
    ######
    score = metrics.######
    scores.#######

X = range(3, 11)
plt.figure(figsize=(8, 6), dpi = 300)
plt.xlabel('k')
plt.ylabel('轮廓系数')
plt.title('轮廓系数图')
plt.plot(X, scores, 'o-')
plt.grid(True)
plt.savefig('轮廓系数图.png')
plt.show()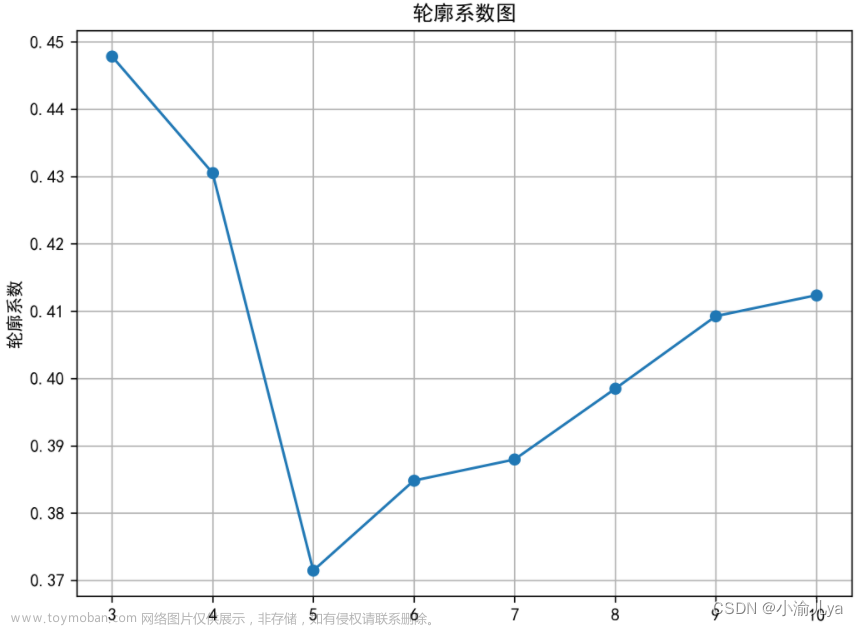

2021 年高教社杯全国大学生数学建模竞赛 E 题中药材的鉴别第一题

根据肘部图，轮廓系数图最后确定k值为3

3.3 数据聚类

km = KMeans(n_clusters = 3) 
km.fit(data) 
print(Counter(km.labels_))  # 打印每个类多少个
print(km.cluster_centers_)  # 中心点

data_1 = data.reset_index() # 把索引转为列
r = pd.concat([data_1['NO'], pd.Series(km.labels_)], axis = 1) 
r.columns = ['NO', '聚类类别']
print(r)

3.4 聚类结果可视化

data_lei0 = data[data['类别']==0]
data_lei1 = data[data['类别']==1]
data_lei2 = data[data['类别']==2]

x0 = data_lei0[0]
y0 = data_lei0[1]
z0 = data_lei0[2]
x1 = data_lei1[0]
y1 = data_lei1[1]
z1 = data_lei1[2]
x2 = data_lei2[0]
y2 = data_lei2[1]
z2 = data_lei2[2]
x3 = [-8.68761271, 10.22622717, -7.66566209]
y3 = [-6.26880974, -0.22269714, 7.70126935]
z3 = [0.04950984, 0.21554457, -0.43296869]
plt.figure(figsize=(8, 6), dpi = 300)
colors=['k', 'b', 'y', 'r']
ax = plt.subplot(111, projection='3d')
ax.plot(x0, y0, z0, 'o', color=colors[0], label='第一类')
ax.plot(x1, y1, z1, 'o', color=colors[1], label='第二类')
ax.plot(x2, y2, z2, 'o', color=colors[2], label='第三类')
ax.plot(x3, y3, z3, '*', color=colors[3], label='中心点')
plt.legend(loc='upper left', numpoints=1, ncol=3, fontsize=8, bbox_to_anchor=(0, 0))
plt.title('聚类效果图')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
plt.savefig('聚类效果图.png')
plt.show()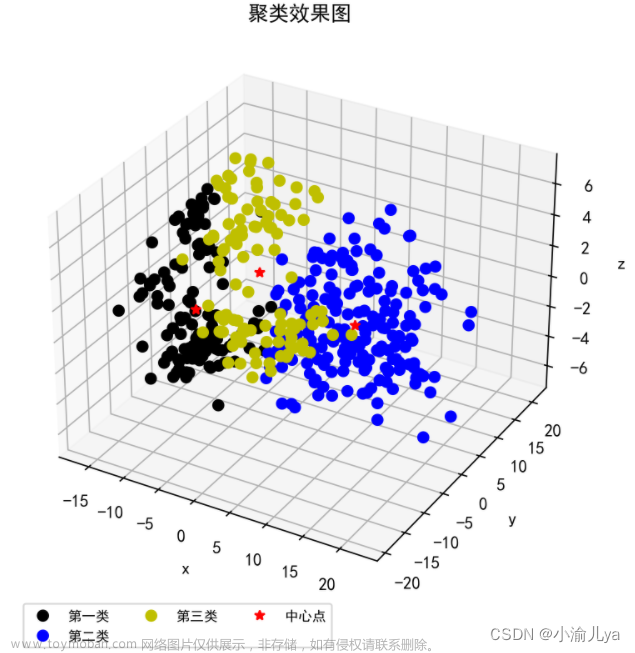

2021 年高教社杯全国大学生数学建模竞赛 E 题中药材的鉴别第一题

到此鉴别药材的种类结束

4. 研究不同种类药材的特征和差异性

研究不同种类药材的特征和差异性

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = 'SimHei' # 设置中文显示
plt.rcParams['axes.unicode_minus'] = False

data = pd.read_excel('聚类.xlsx',index_col = 1)

data_1 = data[data['类别']=='第一类']
data_2 = data[data['类别']=='第二类']
data_3 = data[data['类别']=='第三类']

根据不同种类药材光谱数据均值曲线和不同种类药材光谱数据标准差曲线进行一个初步分析可以看出在峰度、峰数等特征上存在一些差异

4.1 不同种类药材光谱数据均值曲线

plt.figure(figsize=(8, 6), dpi = 300)
plt.xticks(range(652, 4000, 500))
plt.plot(np.mean(data_1), c = 'r', label = '第一类')
plt.plot(np.mean(data_2), c = 'b', label = '第二类')
plt.plot(np.mean(data_3), c = 'k', label = '第三类')
plt.grid(True)
plt.legend()
plt.xlabel('波数(cm^-1)')
plt.ylabel('吸光度(AU)')
plt.title('不同种类药材光谱数据均值曲线')
plt.savefig('不同种类药材光谱数据均值曲线.png')
plt.show()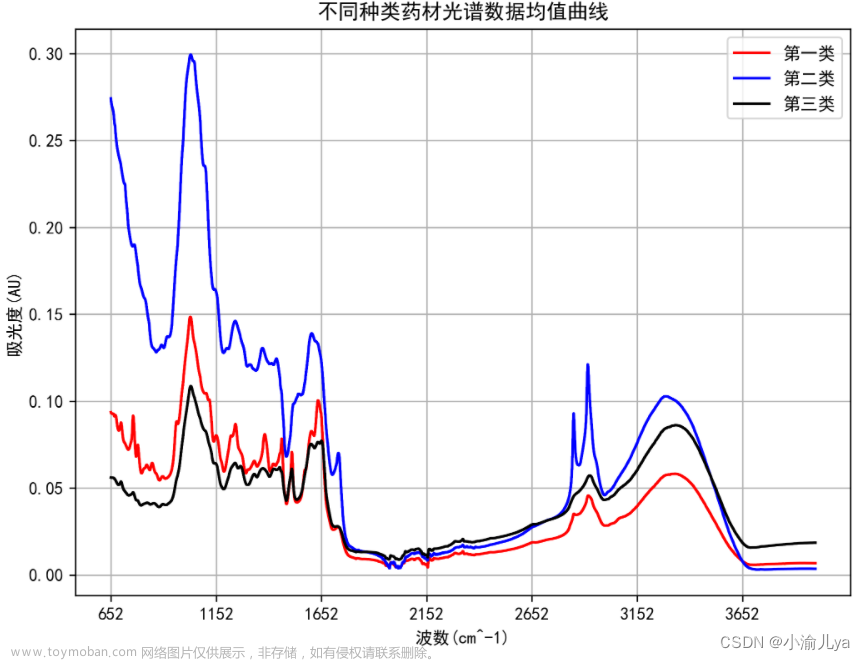

2021 年高教社杯全国大学生数学建模竞赛 E 题中药材的鉴别第一题

4.2 不同种类药材光谱数据标准差曲线图

plt.figure(figsize=(8, 6), dpi = 300)
plt.xticks(range(652, 4000, 500))
plt.plot(np.std(data_1), c = 'r', label = '第一类')
plt.plot(np.std(data_2), c = 'b', label = '第二类')
plt.plot(np.std(data_3), c = 'k', label = '第三类')
plt.grid(True)
plt.legend()
plt.xlabel('波数(cm^-1)')
plt.ylabel('吸光度(AU)')
plt.title('不同种类药材光谱数据标准差曲线')
plt.savefig('不同种类药材光谱数据标准差曲线.png')
plt.show()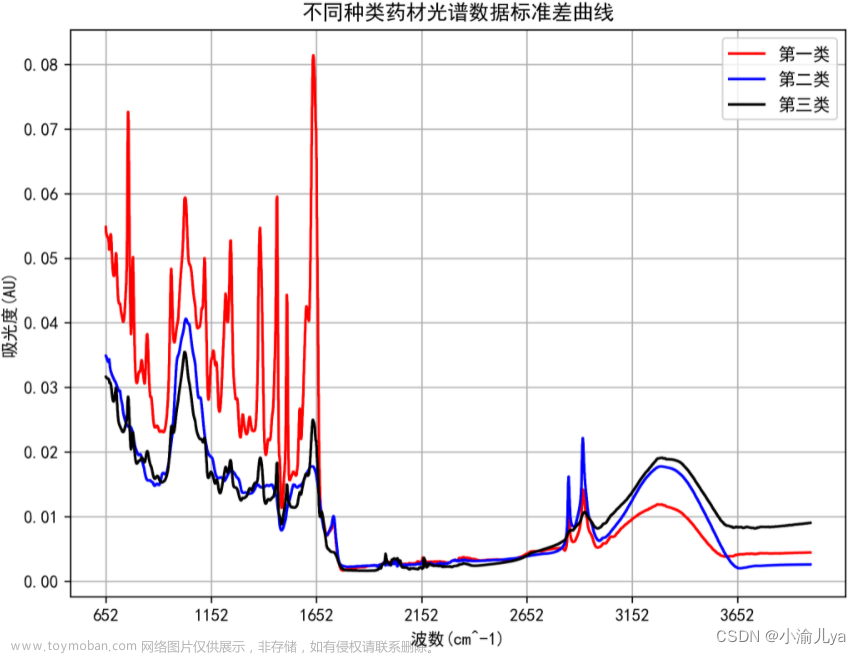

2021 年高教社杯全国大学生数学建模竞赛 E 题中药材的鉴别第一题

4.3 计算每类中药材光谱图的光谱信息散度SID

为进一步探讨不同种类药材的特征和差异性引入一个指标 ‘光谱信息散度SID’

光谱信息散度(SID)用来衡量高光谱图像中两个不同像元之间的相似性。欧氏距离考虑了光谱本身的变动性,能对光谱数据进行更好的评价。

df_1 = pd.DataFrame(np.mean(data_1))
df_2 = pd.DataFrame(np.mean(data_2))
df_3 = pd.DataFrame(np.mean(data_3))
index_0 = range(652, 4000)

def SID(x, y):
    p = np.zeros_like(x, dtype=np.float)
    q = np.zeros_like(y, dtype=np.float)
    Sid = 0
    for i in range(len(x)):
        p[i] = x[i]/np.sum(x)
        ##############
    for j in range(len(x)):
        #############
    return Sid

# 第一类和第二类光谱信息散度（SID）
SID((pd.DataFrame(df_1.values.T, columns = index_0)).values, (pd.DataFrame(df_2.values.T, columns = index_0)).values)

# 0.024393900155562476

# 第一类和第三类光谱信息散度（SID）
SID((pd.DataFrame(df_1.values.T, columns = index_0)).values, (pd.DataFrame(df_3.values.T, columns = index_0)).values)

# 0.06295196780155943

# 第二类和第三类光谱信息散度（SID）
SID((pd.DataFrame(df_2.values.T, columns = index_0)).values, (pd.DataFrame(df_3.values.T, columns = index_0)).values)

# 0.1474926576547535

2021 年高教社杯全国大学生数学建模竞赛 E 题中药材的鉴别第一题