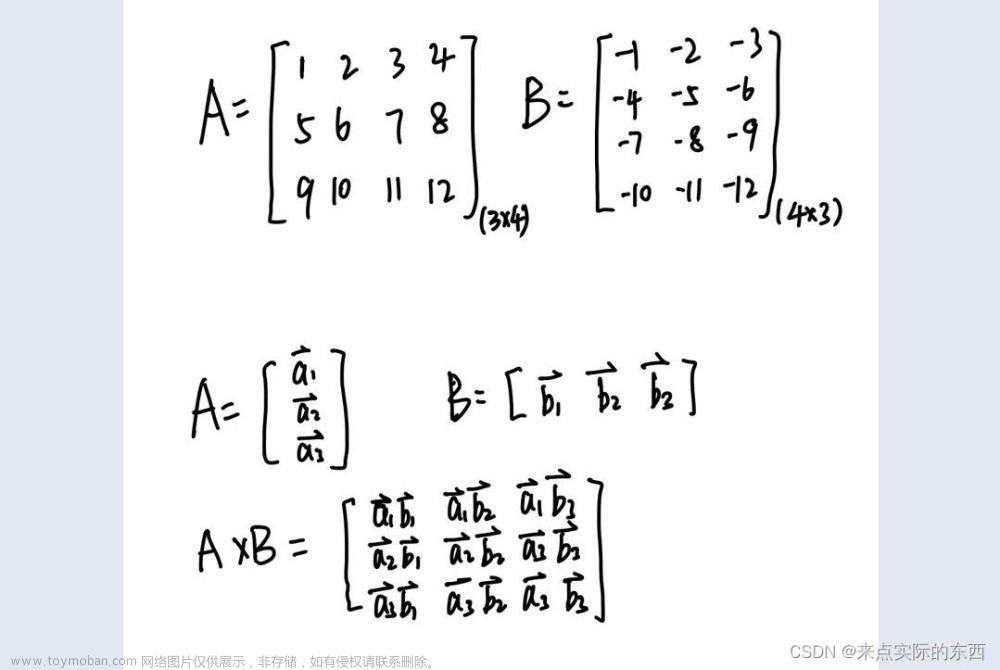
1)两个向量间的投影
如果两个向量垂直,那么满足。但如果两个向量不垂直,我们就将 b 投影到 a 上,就得到了二者的距离,我们也称为向量 b 到直线 a 的误差。这样就有出现了垂直:
(1)

投影向量 p 在直线上,不妨假设 ,那么误差 。带入式(1)中得到:
投影矩阵:
投影矩阵有两个基本性质。
性质一: (投影矩阵为对称矩阵);
性质二: (两次投影结果相同),具体证明直接代公式。
2)向量与平面的投影
如下图所示,有向量 b ,和由向量 a1、a2 线性组合成的列空间(平面)。将向量 b 投影到平面上得到:,下面求解投影矩阵 。

求解步骤和上面一样,只是由直线变为了平面空间,以前假设 ,现在假设:
同理:
又向量 e 垂直于平面,所以:
因为可逆且对称(证明在附录2),所以:
同样的有、
其实,投影就是将向量分解为两部分,一部分(p)投影到矩阵A的列空间中,另一部分(e)投影到了左零空间。文章来源:https://www.toymoban.com/news/detail-459346.html
参考:《Liear Algebra And Its Application》Gilbert Strang文章来源地址https://www.toymoban.com/news/detail-459346.html
附录一:
附录二 :
到了这里,关于投影矩阵推导【线性代数】的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!