图的遍历——深度优先搜索（DFS）与广度优先搜索（BFS）（附带C语言源码）-Toy模板网

这篇具有很好参考价值的文章主要介绍了图的遍历——深度优先搜索（DFS）与广度优先搜索（BFS）（附带C语言源码）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

个人主页：【😊个人主页】
系列专栏：【❤️数据结构与算法】
学习名言：天子重英豪，文章教儿曹。万般皆下品，惟有读书高——《神童诗劝学》

图的遍历——深度优先搜索（DFS）与广度优先搜索（BFS）（附带C语言源码）

系列文章目录

第一章 ❤️ 学前知识
第二章 ❤️ 单向链表
第三章 ❤️ 递归
…

前言

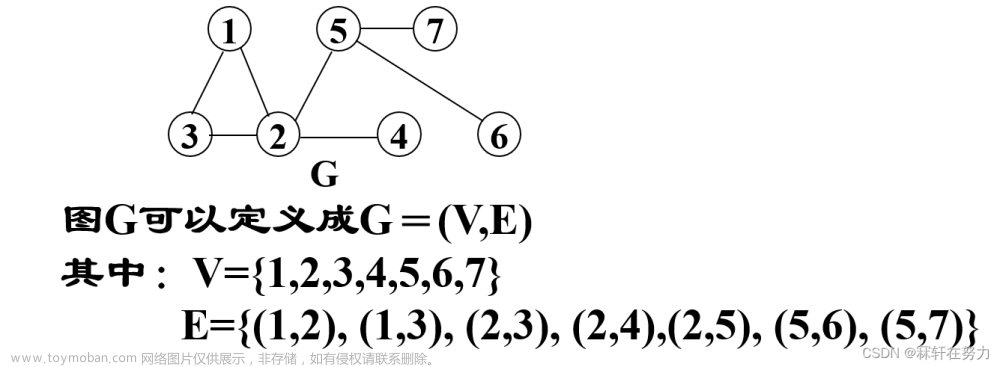
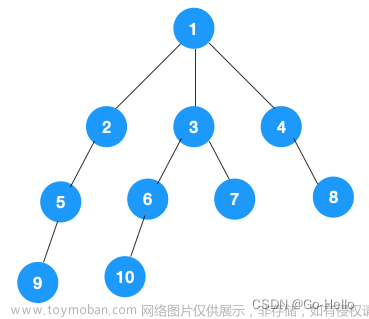
在此之前我们学习过了图的一些基本概念，如同在二叉树中我们有前序遍历，中序遍历，后序遍历一般，在图中也有两种特殊的遍历方式——深度优先遍历与广度优先遍历

深度优先搜索（DFS）

深度优先搜索属于图算法的一种，英文缩写为DFS即Depth First Search.其过程简要来说是对每一个可能的分支路径深入到不能再深入为止，而且每个节点只能访问一次。

深度优先搜索是一种在开发爬虫早期使用较多的方法。它的目的是要达到被搜索结构的叶结点(即那些不包含任何超链的HTML文件) 。在一个HTML文件中，当一个超链被选择后，被链接的HTML文件将执行深度优先搜索，即在搜索其余的超链结果之前必须先完整地搜索单独的一条链。深度优先搜索沿着HTML文件上的超链走到不能再深入为止，然后返回到某一个HTML文件，再继续选择该HTML文件中的其他超链。当不再有其他超链可选择时，说明搜索已经结束。

深度优先搜索沿着一条路径一直搜索下去，在无法搜索时，回退到刚刚访问过的节点。深度优先遍历是按照深度优先搜索的方式对图进行遍历的。

算法原理

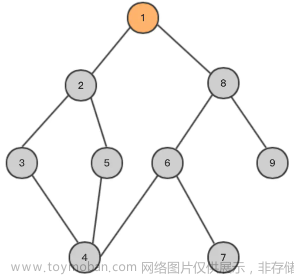
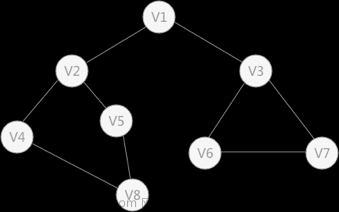
深度优先遍历图的方法是，从图中某顶点v出发:

访问顶点v;
依次从v的未被访问的邻接点出发，对图进行深度优先遍历;直至图中和v有路径相通的顶点都被访问;
若此时图中尚有顶点未被访问，则从一个未被访问的顶点出发，重新进行深度优先遍历，直到图中所有顶点均被访问过为止。

在dfs的方法中传入一个表示当前顶点序号的参数，在dfs方法内部使用一个for循环来检查当前顶点连接的其他邻居，在递归方法中每访问一个节点那么我们就可以使用输出语句来进行输出，输出结果为深度优先搜索访问节点的顺序

搜索算法简而言之就是穷举所有可能情况并找到合适的答案，所以最基本的问题就是罗列出所有可能的情况，这其实就是一种产生式系统。
我们将所要解答的问题划分成若干个阶段或者步骤，当一个阶段计算完毕，下面往往有多种可选选择，所有的选择共同组成了问题的解空间，对搜索算法而言，将所有的阶段或步骤画出来就类似是树的结构。
我们使用递归实现DFS。首先访问起点s，并标记它已经被访问。然后遍历s的邻居节点，如果某个邻居节点w未被访问过，就递归地访问w。这个递归过程会使得我们从s开始尽可能地往下深入，直到遇到死胡同才会回溯到上一个节点继续遍历其他未访问的邻居。执行完所有的递归操作后，我们就完成了整个图的深度遍历。

所有的搜索算法从其最终的算法实现上来看，都可以划分成两个部分──控制结构和产生系统。
图的遍历——深度优先搜索（DFS）与广度优先搜索（BFS）（附带C语言源码）

代码实现（C语言）

#include <stdio.h>
#include <stdlib.h>

#define MAX_VERTEX_NUM 100 // 定义最大的顶点数目

// 定义一个图的数据结构（使用邻接表表示）
typedef struct Graph {
    int V; // 顶点数目
    int** adj_list; // 邻接表
} Graph;

// 创建一条边
int* create_edge(int w) {
    int* edge = (int*) malloc(sizeof(int));
    *edge = w;
    return edge;
}

// 构造函数
Graph* create_graph(int V) {
    Graph* G = (Graph*) malloc(sizeof(Graph));
    G->V = V;
    G->adj_list = (int**) malloc(V * sizeof(int*));
    for (int i = 0; i < V; i++) {
        G->adj_list[i] = NULL;
    }
    return G;
}

// 添加一条边
void add_edge(Graph* G, int v, int w) {
    G->adj_list[v] = create_edge(w);
}

// 释放图的内存
void free_graph(Graph* G) {
    for (int i = 0; i < G->V; i++) {
        if (G->adj_list[i] != NULL) {
            free(G->adj_list[i]);
        }
    }
    free(G->adj_list);
    free(G);
}

// 深度优先搜索算法
void dfs_helper(Graph* G, int v, int visited[]) {
    visited[v] = 1;
    printf("%d ", v);
    int* adj = G->adj_list[v];
    while (adj != NULL) {
        int w = *adj;
        if (visited[w] == 0) {
            dfs_helper(G, w, visited);
        }
        adj = adj + 1;
    }
}

void dfs(Graph* G) {
    // 初始化visited数组
    int visited[MAX_VERTEX_NUM];
    for (int i = 0; i < G->V; i++) {
        visited[i] = 0;
    }
    // 对每个未被访问的顶点调用dfs_helper函数
    for (int i = 0; i < G->V; i++) {
        if (visited[i] == 0) {
            dfs_helper(G, i, visited);
        }
    }
}

int main() {
    Graph* G = create_graph(6);
    add_edge(G, 0, 1);
    add_edge(G, 0, 2);
    add_edge(G, 1, 3);
    add_edge(G, 2, 3);
    add_edge(G, 2, 4);
    add_edge(G, 3, 5);
    dfs(G);
    free_graph(G);
    return 0;
}

注`在这里插入代码片`意，此代码示例中使用一个较简单的图数据结构表示。具体实现时，可以根据实际需要自定义图的数据结构和相关操作。

广度优先搜索

广度优先算法(Breadth-First Search)，同广度优先搜索，又称作宽度优先搜索，或横向优先搜索，简称BFS，是一种图形搜索演算法。简单的说，BFS是从根节点开始，沿着树的宽度遍历树的节点，如果发现目标，则演算终止。广度优先搜索的实现一般采用open-closed表。

BFS是一种盲目搜寻法，目的是系统地展开并检查图中的所有节点，以找寻结果。换句话说，它并不考虑结果的可能位置，彻底地搜索整张图，直到找到结果为止。BFS并不使用经验法则算法。
从算法的观点，所有因为展开节点而得到的子节点都会被加进一个先进先出的伫列中。一般的实作里，其邻居节点尚未被检验过的节点会被放置在一个被称为open的容器中(例如伫列或是链表)，而被检验过的节点则被放置在被称为closed的容器中。(open-closed表)

算法原理

所谓广度，就是一层一层的，向下遍历，层层堵截

访问顶点vi ;
访问vi 的所有未被访问的邻接点w1 ,w2 , …wk ;
依次从这些邻接点(在步骤②中访问的顶点)出发，访问它们的所有未被访问的邻接点; 依此类推，直到图中所有访问过的顶点的邻接点都被访问;

BFS使用一个队列来维护当前正在遍历的节点，首先将起点加入队列，然后只要队列不为空，就从队列中取出一个节点进行拓展（即获取它的邻居节点），依次将这些邻居节点加入队列中。因此，BFS按照离起点的距离逐层遍历，可以求出起点到每个节点的最短路径。
我们先定义了一个队列来维护当前正在遍历的节点，使用数组实现即可。我们还需要记录每个节点是否已经被访问，使用一个数组visited来实现。在BFS算法中，我们每次取出队列的头部节点进行拓展，将其邻居节点加入队列的尾部，并标记它们已经被访问。执行完这些拓展操作后，我们继续从队列头部取出下一个节点进行拓展，直到队列为空。

代码实现（C语言）

#include <stdio.h>
#include <stdlib.h>
#define MAX_VERTEX_NUM 100 // 定义最大的顶点数目

// 定义一个图的数据结构（使用邻接表表示）
typedef struct Graph {
    int V; // 顶点数目
    int** adj_list; // 邻接表
} Graph;

// 创建一条边
int* create_edge(int w) {
    int* edge = (int*) malloc(sizeof(int));
    *edge = w;
    return edge;
}

// 构造函数
Graph* create_graph(int V) {
    Graph* G = (Graph*) malloc(sizeof(Graph));
    G->V = V;
    G->adj_list = (int**) malloc(V * sizeof(int*));
    for (int i = 0; i < V; i++) {
        G->adj_list[i] = NULL;
    }
    return G;
}

// 添加一条边
void add_edge(Graph* G, int v, int w) {
    G->adj_list[v] = create_edge(w);
}

// 释放图的内存
void free_graph(Graph* G) {
    for (int i = 0; i < G->V; i++) {
        if (G->adj_list[i] != NULL) {
            free(G->adj_list[i]);
        }
    }
    free(G->adj_list);
    free(G);
}

// 广度优先搜索算法
void bfs(Graph* G, int s) {
    int visited[MAX_VERTEX_NUM] = {0}; // 记录每个节点是否已经被访问
    int queue[MAX_VERTEX_NUM], head = 0, tail = 0; // 使用队列来存储正在遍历的节点
    visited[s] = 1;
    queue[tail++] = s;
    while (head < tail) {
        int v = queue[head++];
        printf("%d ", v);
        int* adj = G->adj_list[v];
        while (adj != NULL) {
            int w = *adj;
            if (visited[w] == 0) {
                visited[w] = 1;
                queue[tail++] = w;
            }
            adj = adj + 1;
        }
    }
}

int main() {
    Graph* G = create_graph(6);
    add_edge(G, 0, 1);
    add_edge(G, 0, 2);
    add_edge(G, 1, 3);
    add_edge(G, 2, 3);
    add_edge(G, 2, 4);
    add_edge(G, 3, 5);
    bfs(G, 0);
    free_graph(G);
    return 0;
}