定义
动态规划方法通常用来求解最优化问题(optimization problem)。这类问题可以有很多可行解,每个解都有一个值,我们希望寻找具有最优值(最小值或最大值)的解。我们称这样的解为问题的一个最优解(an optimal solution),而不是最优解(the optimal solution),因为可能有多个解都达到最优值。
动态规划与分治问题的区别
分治问题:将问题划分为互不相交的子问题,递归地求解子问题,再将它们的解组合起来,求出原问题的解。
与之相反,动态规划应用于子问题重叠的情况,即不同的子问题具有公共的子子问题(子问题的求解是递归进行的,将其划分为更小的子子问题)。
在这种情况下,分治算法会做许多不必要的工作,它会反复地求解那些公共子子问题。
而动态规划算法对每个子子问题只求解一次,将其解保存在一个表格中,从而无需每次求解一个子子问题时都重新计算,避免了这种不必要的计算工作。
两种方式实现动态规划
根据是否将子问题的解保存到一个表中,分出两种实现动态规划的方式。
方法一:带备忘录的自顶向下法
此方法仍按自然的递归形式编写过程,但过程会保存每个子问题的解(通常保存在一个数组或散列表中)。当需要一个子问题的解时,过程首先检查是否已经保存过此解。如果是,则直接返回保存的值,从而节省了计算时间,否则,按通常方式计算这个子问题。我们称这个递归过程是带备忘的(memoized),因为它“记住”了之前已经计算出的结果。
方法二:自底向上法
此方法仍按自然的递归形式编写过程,但过程会保存每个子问题的解(通常保存在一个数组或散列表中)。当需要一个子问题的解时,过程首先检查是否已经保存过此解。如果是,则直接返回保存的值,从而节省了计算时间,否则,按通常方式计算这个子问题。我们称这个递归过程是带备忘的(memoized),因为它“记住”了之前已经计算出的结果。
本质核心
动态规划的本质上是,如何实现对每个子子问题只求解一次,获得最后的结果。
解题步骤
注意状态转移公式(递推公式)是很重要,但动态规划不仅仅只有递推公式。充分理解如何初始化dp数组已经递推公式才是解决动态规划问题的关键。
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
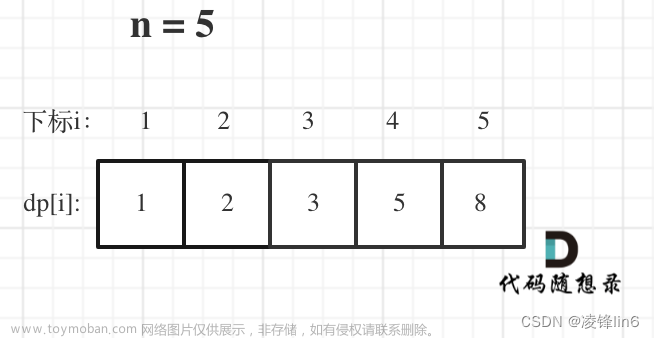
- 举例推导dp数组
常见题型划分
- 基础入门题
- 背包问题
- 打家劫舍
- 股票问题
- 子序列问题
本篇介绍动态规划的理论基础,后面更加详细就题目本身分析与理论验证。文章来源:https://www.toymoban.com/news/detail-459536.html
ps:计划每日更新一篇博客,今日2023-05-11,日更第二十五天。
昨日更新:
花式反转字符串文章来源地址https://www.toymoban.com/news/detail-459536.html
到了这里,关于动态规划理论基础的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!