基于邻接矩阵的有向图的广度优先遍历(BFS)和深度优先遍历(DFS)算法-Toy模板网

这篇具有很好参考价值的文章主要介绍了基于邻接矩阵的有向图的广度优先遍历(BFS)和深度优先遍历(DFS)算法。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

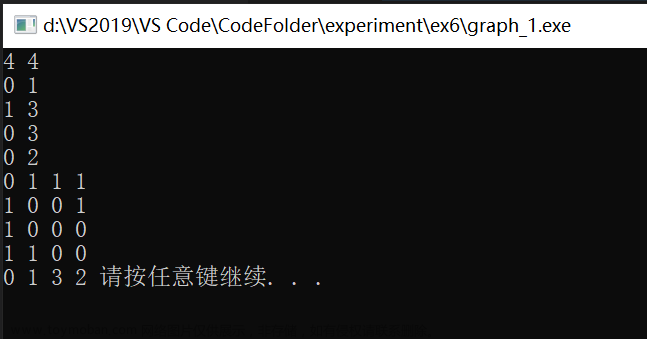
BFS

概念：广度优先遍历算法是图的另一种基本遍历算法，其基本思想是尽最大程度辐射能够覆盖的节点，并对其进行访问。
以迷宫为例，广度优先搜索则可以想象成一组人一起朝不同的方向走迷宫，当出现新的未走过的路的时候，可以理解成一个人有分身术，继续从不同的方向走，，当相遇的时候则是合二为一，那么也就类似于树的层次遍历，当访问完一层后接下去访问，唯一的区别就是图存在回路，为了避免二次访问需要添加一个访问数组，来判断当前节点是否被访问过。

↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓下面给出有向图的例子↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓

基于邻接矩阵的有向图的广度优先遍历(BFS)和深度优先遍历(DFS)算法

那么根据BFS的思想假设以v1作为起始顶点，依次向下遍历顺序为 V1->V0->V2->V4->V3，如果根据树的层次遍历应用在BFS上，当V0遍历完后将V0的邻接点V1 V4 依次入队访问v1再重复以上步骤，当队为空时，遍历完成。这里只是用邻接节点代替了左右孩子的思想，本质还是层次遍历

↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓下面给出具体代码实现↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓文章来源地址https://www.toymoban.com/news/detail-459706.html

void BFS(PGraph G,int v,bool visited [])
{
	//广度优先遍历图,v-->首个要遍历的节点
	printf(" %d ",v);
	visited[v] = true; //首个节点已访问 
	Queue Q;
	Init_Queue(&Q); //初始化队列 
	En_Queue(&Q,v); //首个元素入队
	while(!is_Empty(&Q)) //队列非空 
	{
		int ver = out_Queue(&Q); //获取首个节点
		for(int w = firstArc(G,ver);w>=0;w=adjArc(G,ver,w))
		{ // firstArc

到了这里，关于基于邻接矩阵的有向图的广度优先遍历(BFS)和深度优先遍历(DFS)算法的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！