0.本系列目的
理解与运用LQR
参考教程
matlab动力学建模与simscape验证
https://www.bilibili.com/video/BV1h44y1m7ca/
笔者是跟着B站上这个教程做的,收获颇丰。如果你和笔者一样,之前从未接触过simscape,那么up的讲解一定会让你对simscape的使用有了初步了解。 【强烈推荐观看】
1 理解
见上一期LQR的理解与运用 第一期——理解篇
2 运用
在solidworks上创建一阶倒立摆模型并导出
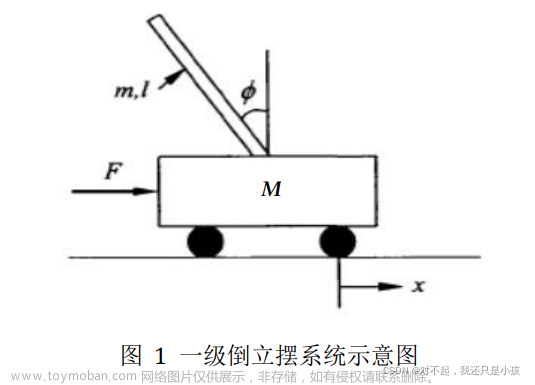
所需建立的模型如下图所示
- 创建步骤
- 创建两个零件,分别代表
滑块和杆子 - 新建装配体将两个零件按照适当配合进行装配,如图

后面在matlab里可以单独设置每个零件的质量,因此不用太在意滑块和杆子的尺寸 参考这篇
这里一共进行了四处配合,分别限制了滑块y,z方向移动,以及令摆杆边线与滑块突起处重合【即同轴心】,以及限制了滑块的滑动范围(如图所示滑块长度为400mm;并限制滑块的移动范围在0~40000mm之间,并把滑块放到了20000mm处)
这样整个机构就只有滑块的运动副和摆杆的转动副两个自由度了
但是后来笔者发现这么做这个插件并不会识别到滑块的运动副,而是会认为滑块是固定的,因此删去了第四个配合
- 倒立摆模型中,初始状态应该保证杆子竖直向上,如上图
为了实现竖直效果,可以先加一个配合,使摆杆的侧面与滑块的侧面平行,然后调整滑块位置,最后删除该配合
-
如果需要导出urdf模型,你需要额外设置每个关节的轴和运动类型【参考链接】
如果需要导出xml 模型,可以直接导出,不需要进行额外设置【参考链接】 -
按照上述导出xml模型的参考链接,修改模型的重力方向,各零件质量并添加观测值(位移 x x x, θ \theta θ,速度 v v v, ω \omega ω)
最好同时修改零件的颜色,不然模型颜色和背景色一致,将很难分辨
也可以在matlab中导入模型后再设置
一阶倒立摆的模型及物理公式推导
模型介绍
本篇使用的一阶倒立摆模型具有两个自由度,一个是绕轴枢转动的转动副,一个是滑块的移动副;
且该模型仅具有一个驱动,即移动副所对应轴,驱动作用效果用作用力F体现
该模型仅有两个稳定点,分别在 θ = 0 ° \theta=0° θ=0°和 θ = 180 ° \theta=180° θ=180°时。
但是在后面仿真时,当摆杆处以恒定驱动作为扰动时, θ \theta θ的稳定值会变化
模型推导
采用以下模型
变量声明
| 物理量 | 符号 |
|---|---|
| 滑块质量 | M M M |
| 摆杆质量 | m m m |
| 摆杆转动轴心到杆质心长度【半杆长】 | l l l |
| 摆杆在转轴处转动惯量 | J J J |
| 小车受到外力 | F F F |
| 小车位置 | x x x |
| 摆杆与竖直方向夹角【本文顺时针为正】 | θ \theta θ |
模型推导方法
看【工具篇】拉格朗日动力学建模及系统设置初值求变量,用牛顿-欧拉公式或者拉格朗日动力学公式推导
化简方法
完成公式推导后,我们有了以下两个式子【对应工具篇的(6) (7)】:
{
m
g
l
sin
θ
−
m
l
cos
θ
⋅
x
¨
=
(
J
+
m
l
2
)
⋅
θ
¨
−
m
l
sin
θ
⋅
θ
˙
2
+
m
l
cos
θ
⋅
θ
¨
+
(
M
+
m
)
⋅
x
¨
=
F
\left\{\begin{array}{l} {m g l \sin \theta}-{m l \cos\theta} \cdot\ddot{x}=(J+{m l^2 }) \cdot\ddot{\theta} \\\\ -ml\sin\theta\cdot \dot{\theta}^{2}+m l \cos\theta\cdot\ddot{\theta}+(M + m)\cdot{\ddot{x}}=F \end{array}\right.
⎩
⎨
⎧mglsinθ−mlcosθ⋅x¨=(J+ml2)⋅θ¨−mlsinθ⋅θ˙2+mlcosθ⋅θ¨+(M+m)⋅x¨=F
进行化简,在平衡点附近,有
θ
˙
≈
0
cos
θ
≈
1
sin
θ
≈
θ
\dot{\theta} \approx 0 \quad \cos \theta \approx 1 \quad \sin \theta \approx \theta
θ˙≈0cosθ≈1sinθ≈θ
化简后,两方程如下:(输入
u
=
F
u=F
u=F)
{
(
J
+
m
l
2
)
θ
¨
−
m
g
l
θ
=
−
m
l
x
¨
(
M
+
m
)
x
¨
+
m
l
θ
¨
=
u
\left\{\begin{array}{l} \left(J+m l^{2}\right) \ddot{\theta}-m g l \theta=-m l \ddot{x} \\ (M+m) \ddot{x}+m l \ddot{\theta}=u \end{array}\right.
{(J+ml2)θ¨−mglθ=−mlx¨(M+m)x¨+mlθ¨=u
取:
x
=
[
x
1
x
2
x
3
x
4
]
=
[
θ
θ
˙
x
x
˙
]
,
u
=
F
x=\left[\begin{array}{l} x_{1} \\ x_{2} \\ x_{3} \\ x_{4} \end{array}\right]=\left[\begin{array}{c} \theta \\ \dot{\theta} \\ x \\ \dot{x} \end{array}\right],u=F
x=
x1x2x3x4
=
θθ˙xx˙
,u=F
根据上面的两个方程,化简二元一次方程,可得
x
¨
,
θ
¨
\ddot x,\ddot \theta
x¨,θ¨
{
x
˙
1
=
x
2
x
˙
2
=
m
g
l
(
M
+
m
)
J
(
M
+
m
)
+
M
m
l
2
x
1
+
−
m
l
J
(
M
+
m
)
+
M
m
l
2
u
x
˙
3
=
x
4
x
˙
4
=
−
m
2
g
l
2
J
(
M
+
m
)
+
M
m
l
2
x
1
+
J
+
m
l
2
J
(
M
+
m
)
+
M
m
l
2
u
\left\{\begin{array}{l} \dot{x}_{1}=x_{2} \\ \dot{x}_{2}=\frac{m g l(M+m)}{J(M+m)+M m l^{2}} x_{1}+\frac{-m l}{J(M+m)+M m l^{2}} u \\ \dot{x}_{3}=x_{4} \\ \dot{x}_{4}=\frac{-m^{2} g l^{2}}{J(M+m)+M m l^{2}} x_{1}+\frac{J+m l^{2}}{J(M+m)+M m l^{2}} u \end{array}\right.
⎩
⎨
⎧x˙1=x2x˙2=J(M+m)+Mml2mgl(M+m)x1+J(M+m)+Mml2−mlux˙3=x4x˙4=J(M+m)+Mml2−m2gl2x1+J(M+m)+Mml2J+ml2u
结论
因此状态方程中
A
、
B
、
C
、
D
A、B、C、D
A、B、C、D四个矩阵的表达式可求出
A
=
[
0
1
0
0
−
m
g
l
(
M
+
m
)
J
(
M
+
m
)
+
M
m
l
2
0
0
0
0
0
0
1
−
m
2
g
l
2
J
(
M
+
m
)
+
M
m
l
2
0
0
0
]
A=\left[\begin{array}{cccc} 0 & 1 & 0 & 0 \\ \frac{-m g l ( M + m )}{J(M+m)+M m l^{2}} & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ \frac{-m^{2} g l^{2}}{J(M+m)+M m l^{2}} & 0 & 0 & 0 \end{array}\right]
A=
0J(M+m)+Mml2−mgl(M+m)0J(M+m)+Mml2−m2gl2100000000010
B = [ 0 − m l J ( M + m ) + M m l 2 0 J + m l 2 J ( M + m ) + M m l 2 ] B=\left[\begin{array}{l} 0\\ \frac{- m l}{J(M+m)+M m l^{2}} \\ 0 \\ \frac{J+m l^{2}}{J(M+m)+M m l^{2}} \end{array}\right] B= 0J(M+m)+Mml2−ml0J(M+m)+Mml2J+ml2
C = [ 1 0 0 0 0 0 1 0 ] C=\left[\begin{array}{llll} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{array}\right] C=[10000100]
D = 0 D=0 D=0
根据模型求LQR的K值
g = 9.80665;
m = 5; % 摆杆质量
M = 1; % 滑块质量
l = 0.18; % 半杆长
J = 1/3 * m * (2 * l)^2;
% ------------------------------------
A21 = m*g*l*(M+m)/(J*(M+m)+M*m*l^2)
A41 = -m^2*g*l^2/(J*(M+m)+M*m*l^2)
A = [0 1 0 0;
A21 0 0 0;
0 0 0 1;
A41 0 0 0];
% [theta, dtheta, x, dx]
B2 = -m*l/(J*(M+m)+M*m*l^2);
B4 = (J+m*l^2)/(J*(M+m)+M*m*l^2);
B = [0;B2;0;B4];
C=[1 0 0 0;0 0 1 0];
D=[0;0];
% ------------------------------------
%% sys = ss(A,B,C,D)
eig(A)
%% Qc=ctrb(A,B)
%% rank(Qc)
Qb=obsv(A,C)
rank(Qb)
% ------------------------------------
Q = [100 0 0 0
0 1 0 0
0 0 10 0
0 0 0 1];
R = 0.1;
K = lqr(A,B,Q,R)
% ------------------------------------
Ac=A-B*K;
x0 = [0;0;0;0]; %初始状态
t = 0:0.05:20;
u = zeros(size(t));
[y,x]=lsim(Ac,B,C,D,u,t,x0);
plot(t,y);
matlab仿真的实现流程与步骤
准备步骤
这一部分操作如果看不懂可以参考上文中提到的 打开xml的链接。
正确导入xml模型
这里令滑块质量
M
=
1
k
g
M=1 kg
M=1kg,摆杆质量
m
=
5
k
g
m=5kg
m=5kg,仿真时间设置为
20
s
20s
20s,修改重力方向,添加观测值(位移
x
x
x,
θ
\theta
θ,速度
v
v
v,
ω
\omega
ω)
完成后效果如图
运行后输出结果如图【位移的单位是10^-13,目前可忽略】
这里看到theta的值大约是
π
\pi
π,因此要在模型中减去一个常数
π
\pi
π【因为初始情况下theta应该是0】
此外,应该保证 θ \theta θ和 x x x的正方向和我们建模时的正方向相同,上面建模时我们将顺时针方向的 θ \theta θ视为正值,而matlab默认以逆时针为正,因此需要对 θ \theta θ乘负号; x x x的方向一致
此处两个值的正负建议读者自行验证,否则到时候LQR算出来的K值,还需要修改其中两个维度的正负号才能符合模型

此外本文模型杆子质心到转轴距离 l = 0.18 m l=0.18m l=0.18m【注意是杆长的一半!】
设置扰动及输入
为转动轴和移动副设置输入【actuator】
-
转动副
输入为转矩【Torque】,而动量设置为自动计算。
这里的输入不可控,因此设置为0,或者设置成白噪声,以模拟干扰如图所示

设置扰动的方法补充说明
事实上,这种扰动的设置方法并不科学,因为这种方法是直接加在关节上的,这份力矩还是会对系统产生作用【是内力不是外力,我们要模拟的是外力】
举个例子
比如把开关拨到常数档,然后给一个较小的常数(如:0.5)
设置好K值这些后,再进行模拟,就会出现一些很反常的现象,如:
这是因为给了摆杆一个力矩为0.5的转矩,与滑块的外力平衡了 -
移动副
输入为力【Force】,而动量设置为自动计算。
这里的输入根据LQR计算,将输入线先拉远一点,到时候要将里面封装成一个模块如图所示

封装模块并实现LQR控制
LQR控制指的就是输入满足 u = K x u =K x u=Kx过程的控制,详见下文
-
封装模块
在四个输出处另外设置四个output
【注:此图及后面的图还没对 θ \theta θ和 ω \omega ω进行系数矫正,是因为截图是还没注意到这个错误】
然后将 除了一个input和四个output的全部模块 封装成一个子系统

-
填入LQR的K值
根据四个自变量的顺序,调整K的顺序,满足 u = K x u =K x u=Kx删掉外面的四个
output模块和一个input模块,加入一个Mux模块和Gain模块,将K值填入第一个Gain模块的增益上,并把乘法形式改成矩阵 K*u
再加一个反馈模块,用来强调 u = K x u=Kx u=Kx;通过ctrl+r改变Gain模块方向,最后效果如图
运行程序
出于不知道什么原因,matlab中lqr求出的K值不能直接用在模块中,应该在后两位乘上
−
1
-1
−1,(或者前两位乘上
−
1
-1
−1,并在gain处乘
−
1
-1
−1。
笔者认为,跟建模时自己将
θ
\theta
θ设置成顺时针为正有关系,但不确定这个猜想是否正确
若不这么设置,就会出现以下情况:

【如图,越来越跟不上,因为后两维
x
,
x
˙
x,\dot x
x,x˙成正反馈了,越跑越大】
能控,但控得不多((
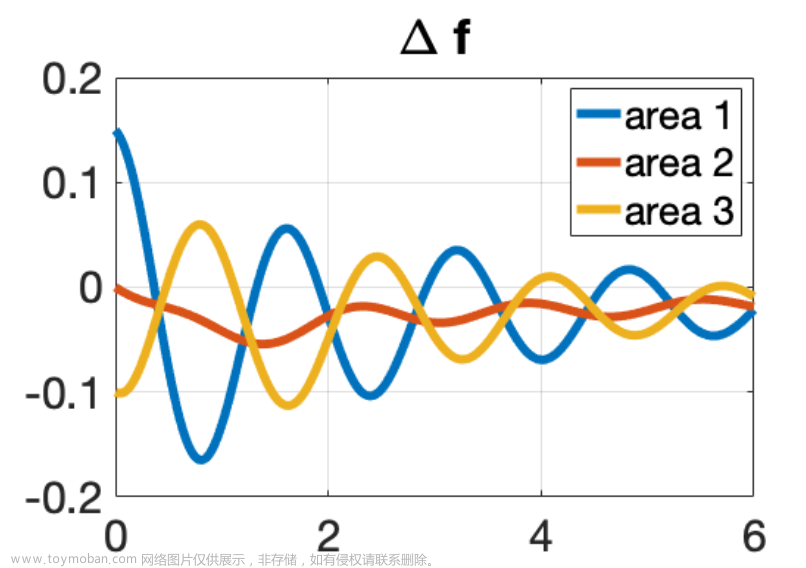
调整好后,效果如下【笔者换了个模型,看得能直观些】


模型位移等值不太稳定的原因是,该模型中一直在持续给干扰,如果把这个干扰改成阶跃的,那么曲线会更加好看
后续操作
接下来能做的操作其实不多了:
- 修改仿真时间【没啥用】
- 调参:根据模型控制情况调整扰动的强度【修改左上角随机干扰的系数】
- 调参:双击Scope观察几个变量的变化情况,根据变化情况修改LQR中的QR权重矩阵,得到新的K
- 改进扰动方式【重中之重,现在的现象是“反直觉”的】
- 了解LQR怎么设置稳态误差,从而实现倒立摆稳定时x的位置可控
到此,matlab搭建物理仿真模型的过程几乎完全结束了,上面标红的两个部分笔者还没找到合适的解决方法,求大佬指点!
项目代码
https://gitee.com/hitszwowow/pendulum-dynamics-system
如果觉得有用的话点个赞和收藏呗🥺文章来源:https://www.toymoban.com/news/detail-459711.html
------------分割线-------------
我的习惯是最新的一篇文章会加一个“仅关注可见”,方便我了解真实“阅读量”。
(如果觉得被骗关注了可以取关哈哈哈文章来源地址https://www.toymoban.com/news/detail-459711.html
到了这里,关于LQR的理解与运用 第二期——一阶倒立摆在matlab上的LQR实现的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!