二项分布习题-Toy模板网

这篇具有很好参考价值的文章主要介绍了二项分布习题。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

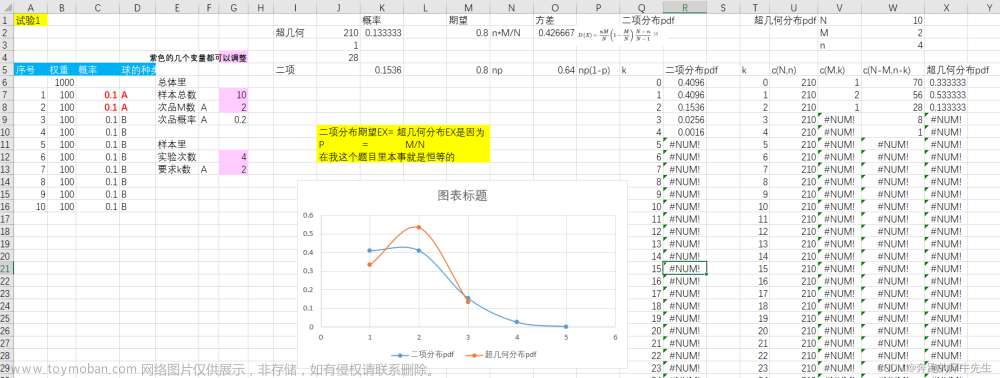
习题：

X ～ B（n，p），n = 5, p = 0.25, k = (0 ～ n)。
将 n , k , p 代入函数：
解：
输出为：
一射手向目标独立地进行了3次射击，每次击中率为0.8，求3次射击中击中目标的次数的分布律，并求3次射击中至少击中2次的概率。
解：
设 X 表示击中目标的次数，则 X = 0， 1， 2， 3。
X 的分布律为：
设射手每次击中目标的概率p = 0.75, 且各次射击相互独立，以 X 记击中目标的次数。
（1）写出 X 的分布律；
（2）求恰击中 3 次的概率；
（3）求至少击中 2 次的概率。
解：
（1）X 的分布律：
没有保留小数点：

保留小数点后三位：
二项分布习题

（2） P{恰击中3次} = P{X = 3} = 0.422
（3） P{至少击中2次} = 1 – P{X = 0} – P{X = 1}
= 1 – 0.004 – 0.047
= 0.949

某一汽车站，每天有大量汽车通过，设每辆车在一天的某段时间内出事故的概率为0.005,在某天的该段时间内有100辆汽车通过，试问出事故的车辆数不少于2的概率是多少？
解：
设 X 为出现事故的车辆数量，由题可知，P = 0.005,
n = 100;
X 的分布律为：

我们只需要知道X = 0，X = 1的概率，用 1 减去就行了。
二项分布习题

（方便计算，保留小数点后6位）
P{X >= 2} = 1 – P{X = 0} – P{X = 1}
= 1 – 0.605770 – 0.304407
= 0.089823

5.经研究表明人们患了某种疾病，有30% 的人不经治疗会自行痊愈，医药公司推出一种新药，随机地选10个患此种病的患者服用了新药，知道其中有9人很快就痊愈了，设各人自行痊愈了，设各人自行痊愈与否相互独立，试推断这些患者是自行痊愈的，还是新药起了作用。
解：
假设新药毫无效果，则一个患者痊愈的概率为 p = 0.3,以X记10个患者中痊愈的病人数，则 X～B（10，0.3）。
X 的分布律为：
二项分布习题

P{X = 9} = 0.000138
P{X >= 9} = P{X = 9} + P{X = 10}
= 0.000138 + 0.000006
= 0.000144
可以看出这个概率很小，几乎不会发生。文章来源地址https://www.toymoban.com/news/detail-459999.html

到了这里，关于二项分布习题的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！