采用邻接矩阵形式存储图,对图进行优先深度搜索,并输出结果。
算法设计
用邻接矩阵存储图首先定义图的邻接矩阵存储结构,其中一维数组vertexs用来表示与顶点有关的信息,二维数组arcs用来表示图中顶点之间的关系。
之后要初始化邻接矩阵,初始化顶点个数以及边的个数,输入数据并且添加权值然后输出矩阵。
深度优先搜索然后遍历,最后输出搜索遍历后的顺序。
深度优先遍历类似于树的先根遍历,是树先根遍历的推广。深度优先遍历是个递归过程,所以这个算法可以用递归实现。从某个结点v出发,进行优先遍历图的算法采用递归的形式说明如下:(1)设置访问标识数组并初始化标识数组。
(2)若访问过顶点,则该标识设置为1,并输出当前顶点。
(3)若某个顶点没有被访问过,则继续进行遍历此顶点。
(4)继续找下一个邻接点,递归递归进行遍历,直到所有顶点都被访问。
设计的函数如下:
| InitG() |
初始化邻接矩阵 |
| Init_Vertex() |
初始化矩阵中的顶点个数 |
| Init_Arc() |
初始化矩阵中的边数 |
| InSerG() |
插入邻接矩阵中的数据 |
| InWeight() |
在矩阵中添加连接顶点之间的信息 ,即为图的权值 |
| Print() |
输出邻接矩阵 |
| Init_DFS() |
深度优先搜索函数 |
| DFS() |
深度优先遍历函数 |
| main() |
主函数用来测试该算法功能 |
源代码:
/************
date:2021-11-27
version:1.0
author:sy
Description:采用邻接矩阵存储图,进行图的深度优先搜索并输出结果
**************/
#include<stdio.h>
#include<stdlib.h>
#define MAXNUM 100
/* 邻接矩阵数据结构体 */
typedef struct {
int vexnum, arcnum; // 图的顶点数和弧数
int vertexs[MAXNUM]; // 存储顶点的一维数组
int arcs[MAXNUM][MAXNUM]; // 邻接矩阵
}graph,*Graph;
typedef struct Arc{
int v1; // 用来存放第一个顶点
int v2; // 用来存放第二个顶点
int weight; // 权值
}*ArcType;
/* 初始化邻接矩阵 */
void InitG(Graph G,int Vertex)
{
G->arcnum = 0; // 初始化为0条边
G->vexnum = Vertex; // 初始化顶点数
int i,j;
for(i=0;i<Vertex;i++)
{
for(j=0;j<Vertex;j++)
{
G->arcs[i][j] = 0;
}
}
}
/* 初始化顶点个数 */
int Init_Vertex()
{
int Vertex;
printf("请输入顶点个数(回车键结束): ");
scanf("%d",&Vertex);
return Vertex;
}
/* 初始化边的数量 */
int Init_Arc()
{
int arc;
printf("请输入边的数量(回车键结束): ");
scanf("%d",&arc);
return arc;
}
void InWeight(Graph G,ArcType T);
/* 开始插入数据 */
void InSerG(Graph G,int edge,int V)
{
int i,j;
if(edge>0) // 边数大于0的时候才插入数据
{
printf("请输入顶点和权值(空格分隔,回车结束)\n");
for(i=0;i<edge;i++)
{
ArcType T; // 分配内存,接受顶点v1,v2和权值
T = (ArcType)malloc(sizeof(struct Arc));
scanf("%d %d %d",&(T->v1),&(T->v2),&(T->weight));
if(T->v1 ==T->v2)
{
printf("无向图邻接矩阵对角线为0,输入错误,结束运行\n");
exit(-1);
}
InWeight(G,T);
}
printf("请输入要创建的顶点(空格隔开,回车结束): \n");
for(j=0;j<V;j++)
{
scanf("%d",&(G->vertexs[j]));
}
}else printf("输入的边数错误");
}
/* 在矩阵中添加连接顶点之间的信息 ,即为图的权值*/
void InWeight(Graph G,ArcType T)
{
G->arcs[T->v1][T->v2] = T->weight;
G->arcs[T->v2][T->v1] = T->weight;
}
/* 输出邻接矩阵 */
void Print(Graph p,int Vertex)
{
int i,j;
for(i=0;i<Vertex;i++)
{
for(j=0;j<Vertex;j++)
{
printf("%4d",p->arcs[i][j]); // 打印邻接矩阵
}
putchar('\n');
}
}
int visited[MAXNUM]; //访问标识数组
void DFS (Graph G,int v,int V); //声明函数
/* 深度优先搜索 */
void Init_DFS (Graph G,int V)
{
int i;
for(i=0;i<V;i++) /*初始化标识数组,全为0*/
{
visited[i] = 0;
}
for(i=0;i<V ;i++) // 检查每一个顶点是否被遍历到
{
if(!visited[i])
DFS (G,i,V); // 开始深度遍历
}
putchar('\n');
}
/*深度优先遍历*/
void DFS (Graph G,int v,int V)
{
int i;
visited[v] = 1;
printf("%d ",G->vertexs[v]); // 输出当前顶点
for(i=0;i<V ;i++)
{
if(!visited[i] && G->arcs[v][i] != 0) // 如果当前顶点的邻近点存在,且没有遍历过
{ // 则继续递归遍历
DFS ( G,i,V ); // 递归遍历当前顶点的邻近点
}
}
}
int main()
{
int Vernum;
int arc;
Graph P; // 邻接矩阵头节点指针
Vernum = Init_Vertex(); /*创建邻接矩阵*/
arc = Init_Arc();
P = (Graph)malloc(sizeof(graph)); //分配存储空间
P->vexnum = Vernum; // 记录顶点个数
P->arcnum = arc; // 记录边的个数
InitG(P,Vernum); // 初始化邻接矩阵
InSerG(P,arc,Vernum); // 插入数据
printf("无向图邻接矩阵如下:");
printf("\n---------\n\n");
Print(P,Vernum);
printf("\n---------\n");
printf("深度优先搜索遍历邻接矩阵结果为:\n");
Init_DFS (P,Vernum);
return 0;
}
测试
在这里输入顶点需要从0开始,因为数组下标是从[0][0]开始的。
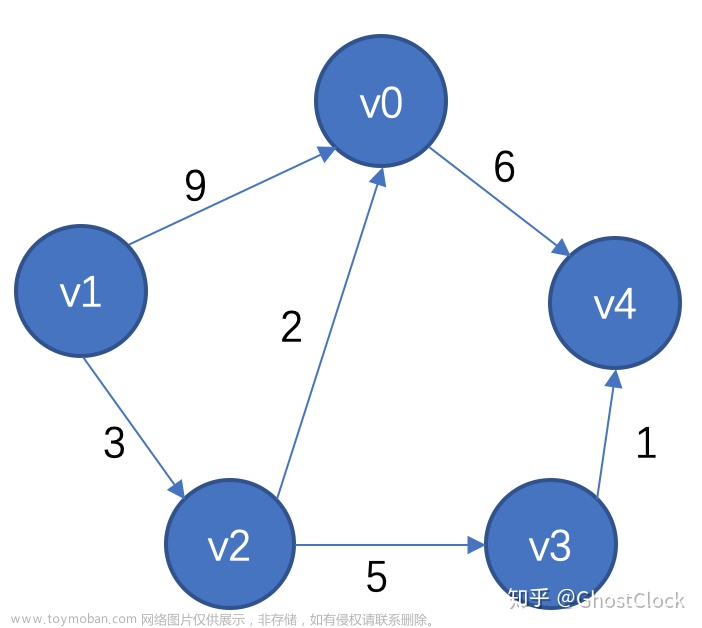
构造一颗无向图如下:

深度优先遍历搜索遍历的结果为:1 2 4 3 5
测试结果如下:文章来源:https://www.toymoban.com/news/detail-460201.html
 文章来源地址https://www.toymoban.com/news/detail-460201.html
文章来源地址https://www.toymoban.com/news/detail-460201.html
到了这里,关于邻接矩阵存储图并深度优先搜索遍历的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!





![[数据结构]:25-图深度优先遍历(邻接矩阵)(C语言实现)](https://imgs.yssmx.com/Uploads/2024/01/409363-1.png)





