【verilog】6位二进制数加法器-Toy模板网

这篇具有很好参考价值的文章主要介绍了【verilog】6位二进制数加法器。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

实验目的

1：掌握无符号二进制数加法器的设计方法。

2：掌握使用Modelsim对verilog程序进行仿真和验证的方法。

实验原理与内容

实验原理

二进制加法器由全加器构成，全加器功能和电路图如下图所示。

【verilog】6位二进制数加法器

全加器对两个1位二进制数和1位来自低位的进位做加法运算，产生1位和和1位向更高位的进位。图中（a）是全加器的真值表，描述了全加器输入和输出之间的加法运算关系。图（b）为根据真值表得到的卡诺图和逻辑表达式。图（c）是全加器的门电路结构。

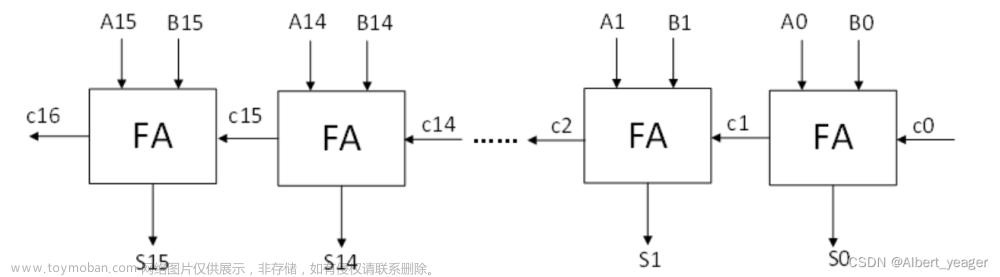
由多个全加器可以构成多位二进制数加法器，其电路图如下图所示。图中每一位全加器的低位进位输入连接更低位的相邻全加器的进位输出，每一位全加器的进位输出连接更高位相邻全加器的进位输入。通过全加器串联的方式实现了两个n位二进制数的加法操作。

【verilog】6位二进制数加法器

实验内容

本实验使用verilog描述、modelsim仿真调试、Quartus II综合下载来完成设计实现6位二进制数加法器电路的内容。该加法器对两个6位二进制数输入进行加法操作，求和结果输出为7位二进制数。2个6位二进制数通过12个拨码开关来输入，7位二进制数的和通过LED灯输出。

实验过程

Modelsim

1 打开Modelsim软件，新建一个工程。

2 建完工程之后，再新建一个verilog文件，打开verilog编辑器对话框。

3 按照所设计电路结构，在verilog编辑窗口编写verilog程序。编写完verilog程序后，保存起来，代码如下图。

【verilog】6位二进制数加法器

4 对自己编写的verilog功能模块，用verilog编写测试模块，可以和功能模块在同一个文件里，也可以新建一个verilog文件。测试模块语句如下图。

【verilog】6位二进制数加法器

5 测试模块产生功能模块的输入的全部取值组合，并对功能模块实例化。进行编译仿真调试，观察仿真波形，根据功能模块输入和输出的对应关系来判断程序是否出错。对程序的错误进行修改，直到仿真波形正确为止，仿真波形图如下图。

【verilog】6位二进制数加法器

QUARTUSII

打开QUARTUSII软件，新建一个工程。
编译综合工程，依照拨码开关和LED灯与FPGA的管脚连接表（参照实验箱用户手册）进行管脚分配。分配完成后，再进行全编译一次，以使管脚分配生效。
建完工程之后，把用Modelsim仿真调试正确的功能模块文件加入该工程（注意这里不需要加测试模块，它仅用于Modelsim仿真）。

【verilog】6位二进制数加法器

4.用下载电缆通过JTAG口将对应的sof文件加载到FPGA中。观察实验结果是否与自己的设计思想一致。

【verilog】6位二进制数加法器

实验总结

通过实验原理得出逻辑表达式，编写Verilog硬件代码，然后通过了ModelSim的波形仿真，在Quartus中再次进行仿真后，将引脚分配好，然后将程序下载至硬件，通过拨动拨动开关，给出两个6位二进制数进行加法运算，能够通过LED灯的显示得到一个7位的二进制数，实现了六位加法器的要求，这里测试了多个实例，得出的结果均为正确，完成了实验任务。文章来源地址https://www.toymoban.com/news/detail-460295.html

到了这里，关于【verilog】6位二进制数加法器的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！