数据结构实验报告（三）——图的操作和实现-Toy模板网

这篇具有很好参考价值的文章主要介绍了数据结构实验报告（三）——图的操作和实现。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

实验目的

1．掌握图的基本概念、性质与应用问题

2．掌握图的邻接矩阵与邻接表存储方式;

3．掌握图的有关算法，如创建、遍历、连通分量、生成树/最小生成树算法（如Prim、Kruskal算法）等;

实验原理

1.建立与存储

邻接矩阵：采用二维数组来存储顶点之间的相邻关系，若两个顶点之间有直连边，则在数组对应位置赋予相应的权值(自身到自身的权值设置为0)，若两个顶点之间没有直连边,则赋予32267，即int型的最大值，意为无穷大；在输入各边的权值时，写了一个找到顶点对应位置的函数，返回顶点对应的下标，这样输入时就能把权值赋予对应的位置。定义一个结构体,结构体属性包括邻接矩阵、存储顶点信息的数组、边数、顶点数。输出用二重循环即可。

2.遍历

深度优先遍历:

用寻找顶点下标的函数返回‘0’的下标，然后开始遍历。采用递归的方式，在邻接矩阵中，找到第一个邻接边，然后又从另一顶点开始，依次递归下去（访问过的顶点用visited[]数组记录），直到所有顶点均已被遍历。

广度优先遍历:

访问起点的所有邻接点，然后从近到远（即下标从小到大）再访问邻接点的所有邻接点，直到遍历完成。

3最小生成树

普里姆算法：

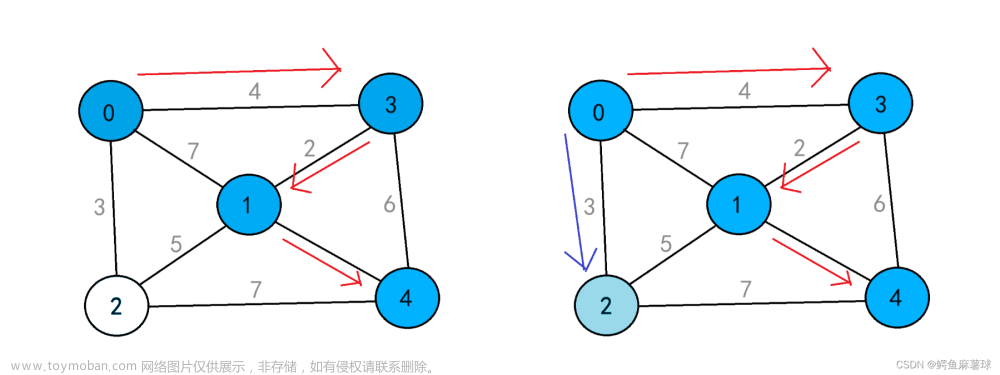
假设有两个集合，一个U，一个V-U，初始时，U里只有起点u1，V-U则为其余顶点，在V-U中寻找权值最小的（u1，vi），然后把vi加入到U，该边对应也加入到最小生成树中，依次类推最终可以得到n个顶点n-1条边的最小生成树。

4.最短路径算法

狄克斯特拉算法：

设有两个集合，一个U，一个V-U；一维数组dist[]用于存储起点到各顶点的最短路径长度；一维数组path[]用于存储最短路径。初始时，U里只有起点u1，V-U则为其余顶点，dist[]数组置为起点的邻接信息。从V-U中寻找较小的顶点（即从dist的值较小的顶点），将它添加到U中，考查该顶点的邻接信息，若该顶点与其他顶点之间有边，则与原定最短路径长度进行比较，新路径插入了中间点，（如新路径0-1-2与原路径0-2比较）更新最短路径长度（如dist[i]）为较小者。重复上述步骤，直到U中包含所有顶点。

实验源码

定义


#define MaxInt 32767        //表示极大值，即∞ 
#define MVNum 100            //最大顶点个数 
typedef char VerTextType;    //顶点的数据类型 
typedef int ArcType;        //边的数据类型

定位元素


//定位邻接表元素 
int locateVexALG(ALGraph G,VerTextType v){
    for(int i=1;i<=G.vexnum;i++){
        if(v==G.vertices[i].data) return i;
    }
}

创建图——邻接矩阵法


//邻接矩阵 
typedef struct{
    VerTextType vexs[MVNum];    //存顶点的数组 
    ArcType arcs[MVNum][MVNum];    //邻接矩阵 
    int vexnum,arcnum;        //顶点、边的数量 
}AMGraph;
typedef struct ArcNode{
    int adjvex;                //该边指向的顶点的位置 
    struct ArcNode *nextarc;//指向下一条边 
}ArcNode;

//创建无向图(邻接矩阵法） 
void createAMUDN(AMGraph &G){
    cout<<"请输入顶点个数：";
    cin>>G.vexnum;
    cout<<"请输入边的个数：";
    cin>>G.arcnum;
    cout<<"请输入顶点名称：";
    for(int i=1;i<=G.vexnum;i++){
        cin>>G.vexs[i];
    }
    for(int i=1;i<=G.vexnum;i++){
        for(int j=1;j<=G.vexnum;j++){
            G.arcs[i][j]=MaxInt;
        }
    }
    cout<<"请输入顶点与边权："<<endl;
    for(int k=1;k<=G.arcnum;k++){
        VerTextType v1,v2;
        ArcType w;
        cin>>v1>>v2>>w;
        int i=locateVexAMG(G,v1);
        int j=locateVexAMG(G,v2);
        G.arcs[i][j]=w;
        G.arcs[j][i]=G.arcs[i][j];//创建有向图就注释掉 
    } 
}

//打印 邻接矩阵法创建的图 
void printAMUDN(AMGraph G){
    for (int i=1;i<=G.vexnum;i++)
    {
        for (int j=1;j<=G.vexnum;j++)
            cout<<G.arcs[i][j]<<"\t";
        cout<<endl;
    }
}

创建图——邻接表法


//邻接表首元结点 
typedef struct VNode{
    VerTextType data;
    ArcNode *firstarc;
}VNode,AdjList[MVNum]; 
//邻接表
typedef struct
{
    AdjList vertices;    //存首元 
    int vexnum,arcnum;    
}ALGraph;

//创建无向图(邻接表法）
void createALUDG(ALGraph &G){
    cout<<"请输入顶点个数："; 
    cin>>G.vexnum;
    cout<<"请输入边的个数：";
    cin>>G.arcnum;
    cout<<"请输入顶点名称：";
    for (int i=1;i<=G.vexnum;i++)
    {
        cin>>G.vertices[i].data;
        G.vertices[i].firstarc=NULL;
    }
    cout<<"请输入边连接的顶点："<<endl; 
    for (int k=1;k<=G.arcnum;k++)
    {
        VerTextType v1,v2;
        cin>>v1>>v2;
        int i=locateVexALG(G,v1);
        int j=locateVexALG(G,v2);
        
        ArcNode *p1,*p2;
        
        p1=new ArcNode;
        p1->adjvex=j;
        p1->nextarc=G.vertices[i].firstarc; //头插 
        G.vertices[i].firstarc=p1;
        
        p2=new ArcNode;
        p2->adjvex=i;
        p2->nextarc=G.vertices[j].firstarc;
        G.vertices[j].firstarc=p2;
    }
} 

//打印 邻接表法创建的图
void printALUDG(ALGraph G){
    for (int i=1;i<=G.vexnum;i++)
    {
        ArcNode *p=G.vertices[i].firstarc;
        cout<<G.vertices[i].data<<"\t";
        while (p)
        {
            cout<<p->adjvex<<"\t";
            p=p->nextarc;
        }
        cout<<endl;
    }
}

DFS遍历——邻接矩阵法和邻接表法


bool visited[MVNum];        //用于DFS 
//DFS遍历（邻接矩阵法）
void Dfs_AM(AMGraph G,int v){
    cout<<v<<" ";
    visited[v]=true;
    for(int i=1;i<=G.vexnum;i++){
        //一条路走到黑 
        if((G.arcs[v][i]!=MaxInt)&&(visited[i]==false)){
            Dfs_AM(G,i);
        }
    }
}

//DFS遍历（邻接表法）
void Dfs_AL(ALGraph G,int v){
    cout<<v<<" ";
    visited[v]=true;
    ArcNode *p;
    p=G.vertices[v].firstarc;
    while(p!=NULL){
        int i=p->adjvex;
        if(!visited[i]) Dfs_AL(G,i);
        p=p->nextarc;
    }
}

计算连通分量


int color[MVNum];            //用于计算连通分量 
int c;                    //连通分量个数
//计算连通分量
void Dfs_countConnect(AMGraph G,int i){
    color[i]=c;
    for(int k=1;k<=G.vexnum;k++){
        if(color[k]==-1 && G.arcs[i][k]!=MaxInt) Dfs_countConnect(G,k);
    }
}
void countConnect(AMGraph G){
    for(int i=0;i<=G.vexnum;i++){
        color[i]=-1;
    } 
    for(int i=1;i<=G.vexnum;i++){
        if(color[i]==-1){
            Dfs_countConnect(G,i);
            c++;
        }
    }
    cout<<"连通分量为："<<c<<endl;
}

最小生成树算法——prim


//最小生成树算法(Prim) 
void MiniSpanTree_Prim(AMGraph G,VerTextType u){
    int k=locateVexAMG(G,u);
    for (int j=1;j<=G.vexnum;j++)
    {
        if (j!=k) closeedge[j]={u,G.arcs[k][j]};
    }
    closeedge[k].lowcost=0;
    int wpl=0;
    for (int i=2;i<=G.vexnum;i++)
    {
        int min=MaxInt;
        for (int j=1;j<=G.vexnum;j++)
        {
            if (closeedge[j].lowcost!=0&&closeedge[j].lowcost<min)
            {
                min=closeedge[j].lowcost;
                k=j;
            }
        }
        wpl+=closeedge[k].lowcost;
        closeedge[k].lowcost=0;
        for (int j=1;j<=G.vexnum;j++)
        {
            if (G.arcs[k][j]<closeedge[j].lowcost)
                closeedge[j]={G.vexs[k],G.arcs[k][j]};
        }
    }
    cout<<"最小生成树总权值为："<<wpl<<endl;
}

最短路径——迪杰斯特拉


//最短路径(迪杰斯特拉)
 void ShortestPath_DIJ(AMGraph G,int v0){
    int n=G.vexnum;
    int ans=0;
    int S[MVNum],D[MVNum],Path[MVNum];
    for (int v=1;v<=n;v++)
    {
        S[v]=false;
        D[v]=G.arcs[v0][v];
        if (D[v]<MaxInt)
            Path[v]=v0;
        else
            Path[v]=-1;
    }
    S[v0]=true;
    D[v0]=0;
    int v,w;
    for (int i=2;i<=n;i++)
    {
        int min=MaxInt;
        for (w=1;w<=n;w++)
        {
            if (!S[w]&&D[w]<min)
            {
                v=w;
                min=D[w];
            }
        }
        S[v]=true;
        for (w=1;w<=n;w++)
        {
            if (!S[w]&&(D[v]+G.arcs[v][w]<D[w]))
            {
                D[w]=D[v]+G.arcs[v][w];
                Path[w]=v;
            }
        }
    }
    for (int i=1;i<=n;i++)
        cout<<G.vexs[v0]<<"---->"<<G.vexs[i]<<"的最短路径为:"<<D[i]<<endl;
}

main


int main(){
    while(true){
        system("cls");
        AMGraph G1;
        ALGraph G2;
        cout<<"1.建立无向图（邻接矩阵）"<<endl;
        cout<<"2.建立无向图（邻接表）"<<endl;
        cout<<"3.DFS遍历（邻接矩阵）"<<endl;
        cout<<"4.DFS遍历（邻接表）"<<endl;
        cout<<"5.计算连通分量"<<endl; 
        cout<<"6.最小生成树——普利姆算法"<<endl;
        cout<<"7.最短路径——迪杰斯特拉算法"<<endl;
        cout<<"0.退出"<<endl;
        cout<<"请选择服务：";
        int ch;
        cin>>ch;
        switch(ch){
            case 1:
                createAMUDN(G1);
                cout<<"邻接矩阵："<<endl;
                printAMUDN(G1);
                break;
            case 2:
                createALUDG(G2);
                cout<<"邻接表："<<endl;
                printALUDG(G2);
                break;
            case 3:
                memset(visited,false,sizeof(visited));
                int v1;
                cout<<"请输入起始点编号：";
                cin>>v1;
                cout<<"深度优先遍历的结果为：";
                Dfs_AM(G1,v1);  //v1为遍历起始点编号 
                cout<<endl;
                break;
            case 4:
                memset(visited,false,sizeof(visited));
                int v2;
                cout<<"请输入起始点编号：";
                cin>>v2;
                cout<<"深度优先遍历的结果为：";
                Dfs_AL(G2,v2);  //v1为遍历起始点编号 
                cout<<endl;
                break;
            case 5:
                countConnect(G1);
                break;
            case 6:
                int v3;
                cout<<"请输入起始点编号：";
                cin>>v3;
                MiniSpanTree_Prim(G1,v3);//1表示起始点 
                break;
            case 7:
                int v4;
                cout<<"请输入起始点编号：";
                cin>>v4;
                ShortestPath_DIJ(G1,v4);//1表示起点
                break;
            case 0:
                exit(0);
                break; 
        } 
        cout<<endl;
        system("pause");
    }    
    return 0;
}

实验结果

创建无向图

邻接矩阵法

邻接表法

其他功能篇幅有限就不展示了

实验心得

一开始想把的MaxInt当成0（为了方便看），后面写普利姆算法计算最小生成树中，在判断最小边时产生bug，最后还是统一赋予一个整型最大值32267。

2.深度遍历中要用到visited这一数组判断各个顶点是否被访问visited=true/false，然后根据临界边递归调用访问下一顶点，直到所有顶点被访问过一次。

3.计算连通分量时，设置color数组，用于森林中的子树“上色”，当同一子树中所有节点被遍历完，计数+1.

创作时在听《龙卷风》

其他博文

数据结构实验报告（一）——线性表、堆栈和队列的操作与实现_队列的基本操作实验报告-CSDN博客https://blog.csdn.net/luohaojia123/article/details/128689896?spm=1001.2014.3001.5501数据结构实验报告（二）——二叉树基本操作_数据结构实验报告二叉树的基本操作-CSDN博客https://blog.csdn.net/luohaojia123/article/details/127905639?spm=1001.2014.3001.5502数据结构实验报告（四）——查找和排序算法_查找算法的设计与实现实验报告-CSDN博客https://blog.csdn.net/luohaojia123/article/details/128690401?spm=1001.2014.3001.5501文章来源地址https://www.toymoban.com/news/detail-460340.html

到了这里，关于数据结构实验报告（三）——图的操作和实现的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！