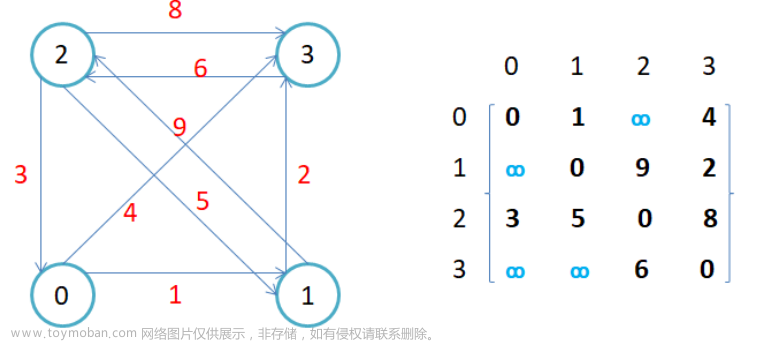
图的遍历
概念:指的是从图中的任一顶点出发,对图中的所有顶点访问一次且只访问一次。
邻接矩阵及邻接表的创建
邻接矩阵及邻接表的创建:
图的存储结构-无向邻接矩阵与无向邻接表(C语言).文章来源地址https://www.toymoban.com/news/detail-460466.html
深度优先遍历(DFS)
邻接矩阵的深度优先遍历
结构定义
#include<stdio.h>
#include<stdlib.h>
#include <stdbool.h> //提供_Bool 类型
typedef char VertexType;
typedef int EdgeType;
#define MAXVEX 100
#define INFINITY 65535
_Bool visited[MAXVEX]; //访问标志的数组
typedef struct {
VertexType vexts[MAXVEX];
EdgeType arc[MAXVEX][MAXVEX];
int numNodes, numEdges;
} MGraph;
邻接矩阵的深度优先遍历操作
/* 邻接矩阵的深度优先遍历操作 */
void DFSTraverse(MGraph G)
{
for (int i = 0; i < G.numNodes; i++) //初始化所有顶点状态为未访问
visited[i] = false;
for (int i = 0; i < G.numNodes; i++)
if (!visited[i]) //对未访问邻接顶点递归调用DFS,如果为连通图仅访问一次
DFS(G, i);
}
邻接矩阵的深度优先递归算法
/* 邻接矩阵的深度优先递归算法 */
void DFS(MGraph G, int i)
{
visited[i] = true; //赋值为真
printf("%c ", G.vexts[i]);
for (int j = 0; j < G.numNodes; j++)
if (G.arc[i][j] != INFINITY && !visited[j]) //对未访问邻接顶点递归调用
DFS(G, j);
}
邻接表的深度优先遍历
结构定义
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
typedef char VertexType; //顶点类型
typedef int EdgeType; //边上权值
#define MAXVEX 100 // 最大顶点数
#define MAXVEX 9
_Bool visited[MAXVEX]; //访问标志的数组
typedef struct EdgeNode { //边表结点
int adjvex; //领接点域,存储对应下标
EdgeType info; //存储权值,如果是非网图可以省略
struct EdgeNode* next; //指向下一个邻接点
}EdgeNode;
typedef struct VertexNode { //顶点结点
VertexType data; //顶点域
EdgeNode* firstedge; //边表头指针
}VertexNode;
typedef struct VertexNode AdjList[MAXVEX]; //邻接表类型
typedef struct {
AdjList adjList;
int numNodes, numEdges; //图当前顶点数与边数
}GraphAdjList;
void CreateALGRAph(GraphAdjList*); //建立图的邻接表结构
int LocateVex(GraphAdjList, VertexType); //查找顶点
void DFSTraverse(GraphAdjList G);
void DFS(GraphAdjList, int); //邻接表的深度优先递归算法
邻接表的深度优先遍历操作
/* 邻接表的深度优先遍历操作 */
void DFSTraverse(GraphAdjList G)
{
for (int i = 0; i < G.numNodes; i++) //初始化所有顶点状态为未访问
visited[i] = false;
for (int i = 0; i < G.numNodes; i++)
if (!visited[i]) //对未访问邻接顶点递归调用DFS,如果为连通图仅访问一次
DFS(G, i);
}
邻接表的深度优先递归算法
/* 邻接表的深度优先递归算法 */
void DFS(GraphAdjList G, int i)
{
EdgeNode* p;
visited[i] = true;
printf("%c", G.adjList[i].data);
p = G.adjList[i].firstedge;
while (p)
{
if (!visited[p->adjvex]) //对未访问邻接顶点递归调用
DFS(G, p->adjvex);
p = p->next;
}
}
广度优先遍历(BFS)
邻接矩阵的广度遍历
结构定义
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
typedef char VertexType; //顶点类型
typedef int EdgeType; //边的权值类型
#define MAXVEX 100
#define INFINITY 65535 //表示无穷大
#define MAXSIZE 9 //队列最大长度
_Bool visited[MAXVEX]; //访问标志的数组
typedef struct {
VertexType vexts[MAXVEX]; //顶点表
EdgeType arc[MAXVEX][MAXVEX]; //邻接矩阵
int numNodes, numEdges; //图当前顶点数与边数
}MGraph;
邻接矩阵的广度遍历算法
/* 邻接矩阵的广度遍历算法 */
void BFSTraverse(MGraph G)
{
int i, j;
Queue Q;
Q.front = Q.rear = 0; //初始化
for (i = 0; i < G.numNodes; i++)
visited[i] = false;
for (i = 0; i < G.numNodes; i++) //对每个顶点做循环
{
if (!visited[i]) //如果未访问过
{
visited[i] = true; //访问
printf("%c ", G.vexts[i]);
EnQueue(&Q, i); //入队
while (Q.front != Q.rear) //队不为空
{
DeQueue(&Q, &i); //队首元素出队
for (j = 0; j < G.numNodes; j++)
{
if (G.arc[i][j] !=INFINITY && !visited[j]) //此顶点存在且边未访问过
{
visited[j] = true;
printf("%c ", G.vexts[j]);
EnQueue(&Q, j); //将此顶点入队
}
}
}
}
}
}
邻接表的广度优先遍历
结构定义
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
typedef char VertexType; //顶点类型
typedef int EdgeType; //边上权值
#define MAXVEX 100 // 最大顶点数
#define MAXSIZE 9 //队列最大长度
_Bool visited[MAXVEX]; //访问标志的数组
typedef struct EdgeNode { //边表结点
int adjvex; //领接点域,存储对应下标
EdgeType info; //存储权值,如果是非网图可以省略
struct EdgeNode* next; //指向下一个邻接点
}EdgeNode;
typedef struct VertexNode { //顶点结点
VertexType data; //顶点域
EdgeNode* firstedge; //边表头指针
}VertexNode;
typedef struct VertexNode AdjList[MAXVEX]; //邻接表类型
typedef struct {
AdjList adjList;
int numNodes, numEdges; //图当前顶点数与边数
}GraphAdjList;
邻接表的遍历算法
/* 邻接表的遍历算法 */
void BFSTraverse(GraphAdjList G)
{
int i;
EdgeNode* p;
Queue Q;
Q.front = Q.rear = 0; //初始化
for (i = 0; i < G.numNodes; i++)
visited[i] = false;
for (i = 0; i < G.numNodes; i++) //对每个顶点做循环
{
if (!visited[i]) //如果未访问过
{
visited[i] = true; //访问
printf("%c ", G.adjList[i].data);
EnQueue(&Q, i); //入队
while (Q.front != Q.rear) //队不为空
{
DeQueue(&Q, &i);
p = G.adjList[i].firstedge;
while (p)
{
if (!visited[p->adjvex])
{
visited[p->adjvex] = true;
printf("%c ", G.adjList[p->adjvex].data);
EnQueue(&Q, p->adjvex);
}
p = p->next;
}
}
}
}
}
广度优先遍历所需队列代码
/* 循环队列顺序储存*/
typedef struct {
int data[MAXVEX];
int front; //头指针
int rear; //尾指针,如果队列不空,指向队列尾元素的下一个位置
}Queue;
/* 入队列 */
void EnQueue(Queue* Q, int e)
{
if ((Q->rear + 1) % MAXSIZE == Q->front) //队满
exit(-1);
Q->data[Q->rear] = e;
Q->rear = (Q->rear + 1) % MAXSIZE;
}
/* 删除头元素,用e返回 */
void DeQueue(Queue* Q, int* e)
{
if (Q->front == Q->rear) //如果为空
exit(-1);
*e = Q->data[Q->front];
Q->front = (Q->front + 1) % MAXSIZE;
}
文章来源:https://www.toymoban.com/news/detail-460466.html
到了这里,关于图的遍历-深度优先遍历与广度优先遍历(C语言)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!