C++——深度优先搜索-Toy模板网

这篇具有很好参考价值的文章主要介绍了C++——深度优先搜索。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

深度优先搜索（Depth-First Search，DFS）是一种用于遍历或搜索图或树的算法。它从起始节点开始，沿着一条路径尽可能深地探索，直到无法继续或达到目标节点，然后回溯到前一节点，继续探索其他路径，直到遍历完所有节点或找到目标。具体过程如下：

1、选择一个起始节点作为当前节点，并标记为已访问。

2、沿着当前节点的未访问邻居节点继续深入。

3、若存在未访问的邻居节点，则选择一个作为当前节点，标记为已访问，并重复步骤2。

4、若不存在未访问的邻居节点，则回溯到上一级节点。

5、重复步骤3和步骤4，直到所有节点都被访问过。

文章来源地址https://www.toymoban.com/news/detail-460723.html

深度优先搜索可以使用递归或显式的栈数据结构来实现。下面是使用递归实现深度优先搜索的简化伪代码：

function DFS(node):
    if node is null:
        return
    
    visit(node)  // 访问当前节点
    
    mark node as visited
    
    for each neighbor of node:
        if neighbor is not visited:
            DFS(neighbor)  // 递归调用深度优先搜索

在深度优先搜索中，每个节点都会被访问且仅被访问一次。它通过递归地遍历每个节点的邻居节点来实现深度搜索。如果某个节点的邻居节点已经被访问过，那么该节点将被跳过。

深度优先搜索的应用广泛，例如在图论中用于寻找连通分量、拓扑排序、寻找路径等。在树的问题中，深度优先搜索可以用于查找树的特定节点或进行树的遍历。

需要注意的是，深度优先搜索可能会陷入无限循环，因此在应用时需要合理设置终止条件和避免重复访问节点。

以下是使用 C++ 实现深度优先搜索（DFS）二叉树的基本代码示例：

#include <iostream>
#include <stack>

using namespace std;

// 二叉树节点定义
struct TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int value) : val(value), left(nullptr), right(nullptr) {}
};

// 深度优先搜索函数
void DFS(TreeNode* root) {
    if (root == nullptr) {
        return;
    }

    stack<TreeNode*> s;
    s.push(root);

    while (!s.empty()) {
        TreeNode* current = s.top();
        s.pop();
        cout << current->val << " "; // 输出当前节点的值

        if (current->right) {
            s.push(current->right); // 将右子节点压入栈中
        }
        if (current->left) {
            s.push(current->left); // 将左子节点压入栈中
        }
    }
}

int main() {
    // 构建二叉树
    TreeNode* root = new TreeNode(1);
    root->left = new TreeNode(2);
    root->right = new TreeNode(3);
    root->left->left = new TreeNode(4);
    root->left->right = new TreeNode(5);
    root->right->left = new TreeNode(6);
    root->right->right = new TreeNode(7);

    cout << "深度优先搜索结果：";
    DFS(root); // 执行深度优先搜索

    return 0;
}

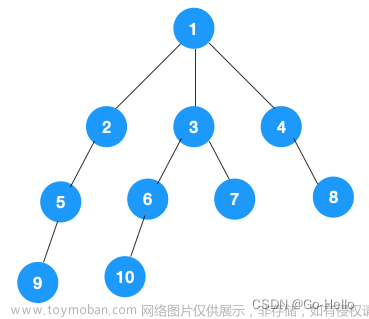
运行以上代码的结果应该是输出深度优先搜索二叉树的节点值。由于二叉树的深度优先搜索的访问顺序是根节点、左子节点、右子节点，因此输出的结果应该是：

深度优先搜索结果：1 2 4 5 3 6 7

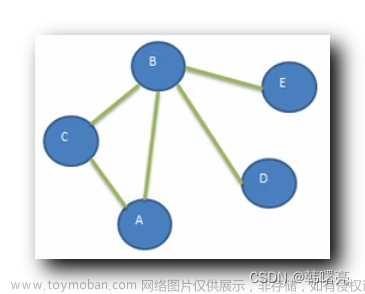
以下是使用深度优先搜索（Depth-First Search，DFS）算法在C++中遍历图的示例代码：

#include <iostream>
#include <vector>
#include <stack>

class Graph {
private:
    int numVertices;          // 图中的节点数
    std::vector<int>* adjList;   // 邻接表

public:
    // 构造函数
    Graph(int numVertices) : numVertices(numVertices) {
        adjList = new std::vector<int>[numVertices];
    }

    // 添加边
    void addEdge(int src, int dest) {
        adjList[src].push_back(dest);
    }

    // 深度优先搜索
    void DFS(int startVertex) {
        std::vector<bool> visited(numVertices, false);   // 标记节点是否被访问
        std::stack<int> stack;                           // 用于DFS的栈

        // 将起始节点入栈并标记为已访问
        stack.push(startVertex);
        visited[startVertex] = true;

        while (!stack.empty()) {
            int currentVertex = stack.top();
            stack.pop();
            std::cout << currentVertex << " ";

            // 遍历当前节点的相邻节点
            for (int neighbor : adjList[currentVertex]) {
                if (!visited[neighbor]) {
                    stack.push(neighbor);
                    visited[neighbor] = true;
                }
            }
        }
    }

    // 析构函数，释放内存
    ~Graph() {
        delete[] adjList;
    }
};

int main() {
    // 创建一个包含5个节点的图
    Graph graph(5);

    // 添加边
    graph.addEdge(0, 1);
    graph.addEdge(0, 2);
    graph.addEdge(1, 3);
    graph.addEdge(2, 3);
    graph.addEdge(2, 4);
    graph.addEdge(3, 4);

    // 从节点0开始进行深度优先搜索
    std::cout << "深度优先搜索结果: ";
    graph.DFS(0);
    std::cout << std::endl;

    return 0;
}

在上述代码中，我们定义了一个Graph类来表示图。使用邻接表作为内部数据结构，使用std::vector<int>* adjList来存储图的邻接表，其中每个向量表示节点的相邻节点列表。

addEdge函数用于向图中添加边，它将目标节点添加到源节点的相邻节点列表中。

DFS函数实现了深度优先搜索算法。它使用一个栈来辅助进行搜索，通过迭代的方式遍历图中的节点。首先，将起始节点入栈并标记为已访问。然后，从栈中弹出当前节点，并访问该节点。接着，遍历当前节点的相邻节点，并将未访问过的相邻节点入栈。不断重复这个过程，直到栈为空。

输出结果为：