基于MATLAB的MIMO信道估计（附完整代码与分析）

目录

一. 介绍

二. MATLAB代码

三. 运行结果与分析

3.1 均方误差（MSE）与训练功率（dB）的关系

3.2 不同信道估计方法性能对比

一. 介绍

本篇将在MATLAB的仿真环境中对比MIMO几种常见的信道估计方法的性能。

有关MIMO的介绍可看转至此篇博客：

MIMO系统模型构建_唠嗑！的博客-CSDN博客

在所有无线通信中，信号通过信道会出现失真，或者会添加各种噪声。正确解码接收到的信号就需要消除信道施加的失真和噪声。为了弄清信道的特性，就需要信道估计。

信道估计有很多不同的方法，但是通用的流程可概括如下：

1. 设置一个数学模型，利用信道矩阵搭建起发射信号和接收信号之间的关系；
2. 发射已知信号（通常称为参考信号或导频信号）并检测接收到的信号；
3. 通过对比发送信号和接收信号，确定信道矩阵中的每个元素。

二. MATLAB代码

一共有四个代码，包含三个函数代码和一个主运行代码。

主运行代码用来产生最后的图像

（1）main.m文件代码

%由于信道数据随机产生，每次运行出的图像可能有略微差异

%初始化
close all;
clear all;


%%设定仿真参数

rng('shuffle'); %产生随机化种子，也可以使用另一函数randn('state',sum(100*clock));


%设定蒙特卡洛仿真的数目
nbrOfMonteCarloRealizations = 1000;

nbrOfCouplingMatrices = 50; %相关矩阵数目

Nt = 8; %发射天线的数量，训练序列的长度
Nr = 4; %接收天线的数量

%训练的总功率
totalTrainingPower_dB = 0:1:20; %单位为dB
totalTrainingPower = 10.^(totalTrainingPower_dB/10); %转为线性范围

%最优化算法
option = optimset('Display','off','TolFun',1e-7,'TolCon',1e-7,'Algorithm','interior-point');


%比较不同的信道估计算法 
%使用蒙特卡洛仿真法
average_MSE_MMSE_estimator_optimal = zeros(length(totalTrainingPower),nbrOfCouplingMatrices,2); %最优训练下的MMSE估计法
average_MSE_MMSE_estimator_heuristic = zeros(length(totalTrainingPower),nbrOfCouplingMatrices,2); %启发训练下的MMSE估计法
average_MSE_MVU_estimator = zeros(length(totalTrainingPower),nbrOfCouplingMatrices,2); %最优训练下的MVU估计法
average_MSE_onesided_estimator = zeros(length(totalTrainingPower),nbrOfCouplingMatrices,2); %单边线性估计法 
average_MSE_twosided_estimator = zeros(length(totalTrainingPower),nbrOfCouplingMatrices,2); %双边线性估计法


%随机信道统计量下的迭代
for statisticsIndex = 1:nbrOfCouplingMatrices
    
    %产生Weichselberger模型下的耦合矩阵V
    %元素均来自卡方分布（自由度为2）
    V = abs(randn(Nr,Nt)+1i*randn(Nr,Nt)).^2;
    V = Nt*Nr*V/sum(V(:)); %将矩阵Frobenius范数设为 Nt x Nr.
    
    %计算耦合矩阵的协方差矩阵
    R = diag(V(:));
    
    R_T = diag(sum(V,1)); %在Weichselberger模型下，计算发射端的协方差矩阵
    R_R = diag(sum(V,2)); %在Weichselberger模型下，计算接收端的协方差矩阵
    
    
    %使用MATLAB内置自带的优化算法，计算MMSE估计法下最优的训练功率分配
    trainingpower_MMSE_optimal = zeros(Nt,length(totalTrainingPower)); %每个训练序列的功率分配向量
    
    for k = 1:length(totalTrainingPower) %遍历每个训练序列的功率分配
        trainingpower_initial = totalTrainingPower(k)*ones(Nt,1)/Nt; %初始设定功率均相等
        
        %使用fmincon函数来最优化功率分配
        %最小化MSE，所有功率均非负
        trainingpower_MMSE_optimal(:,k) = fmincon(@(q) functionMSEmatrix(R,q,Nr),trainingpower_initial,ones(1,Nt),totalTrainingPower(k),[],[],zeros(Nt,1),totalTrainingPower(k)*ones(Nt,1),[],option);
    end
    
    
    %计算功率分配
    [eigenvalues_sorted,permutationorder] = sort(diag(R_T),'descend'); %计算和整理特征值
    [~,inversePermutation] = sort(permutationorder); %记录特征值的order
    
    q_MMSE_heuristic = zeros(Nt,length(totalTrainingPower));
    for k = 1:length(totalTrainingPower) %遍历每个训练功率
        alpha_candidates = (totalTrainingPower(k)+cumsum(1./eigenvalues_sorted(1:Nt,1)))./(1:Nt)'; %计算拉格朗日乘子的不同值
        optimalIndex = find(alpha_candidates-1./eigenvalues_sorted(1:Nt,1)>0 & alpha_candidates-[1./eigenvalues_sorted(2:end,1); Inf]<0); %找到拉格朗日乘子的α
        q_MMSE_heuristic(:,k) = max([alpha_candidates(optimalIndex)-1./eigenvalues_sorted(1:Nt,1) zeros(Nt,1)],[],2); %使用最优的α计算功率分配
    end
    
    q_MMSE_heuristic = q_MMSE_heuristic(inversePermutation,:); %通过重新整理特征值来确定最终的功率分配
    
    
    %计算均匀功率分配
    q_uniform = (ones(Nt,1)/Nt)*totalTrainingPower;
    
    
    %蒙特卡洛仿真初始化
    vecH_realizations = sqrtm(R)*( randn(Nt*Nr,nbrOfMonteCarloRealizations)+1i*randn(Nt*Nr,nbrOfMonteCarloRealizations) ) / sqrt(2); %以向量的形式产生信道 
    vecN_realizations = ( randn(Nt*Nr,nbrOfMonteCarloRealizations)+1i*randn(Nt*Nr,nbrOfMonteCarloRealizations) ) / sqrt(2); %以向量的形式产生噪声
    
    
    %对于每种估计方法计算MSE和训练功率
    for k = 1:length(totalTrainingPower)
        
        %MMSE估计法：最优训练功率分配
        P_tilde = kron(diag(sqrt(trainingpower_MMSE_optimal(:,k))),eye(Nr)); %计算有效功率矩阵
        
        average_MSE_MMSE_estimator_optimal(k,statisticsIndex,1) = trace(R - (R*P_tilde'/(P_tilde*R*P_tilde' + eye(length(R))))*P_tilde*R); %计算MSE
        
        H_hat = (R*P_tilde'/(P_tilde*R*P_tilde'+eye(length(R)))) * (P_tilde*vecH_realizations+vecN_realizations); %使用蒙特卡洛仿真来计算该估计
        average_MSE_MMSE_estimator_optimal(k,statisticsIndex,2) = mean( sum(abs(vecH_realizations - H_hat).^2,1) ); %使用蒙特卡洛仿真来计算MSE
        
        
        %MMSE估计法：启发式训练功率分配MMSE 
        P_tilde = kron(diag(sqrt(q_MMSE_heuristic(:,k))),eye(Nr));  %计算有效训练矩阵
        
        average_MSE_MMSE_estimator_heuristic(k,statisticsIndex,1) = trace(R - (R*P_tilde'/(P_tilde*R*P_tilde' + eye(length(R))))*P_tilde*R); %计算MSE
        
        H_hat = (R*P_tilde'/(P_tilde*R*P_tilde'+eye(length(R)))) * (P_tilde*vecH_realizations + vecN_realizations); %使用蒙特卡洛仿真来计算该估计
        average_MSE_MMSE_estimator_heuristic(k,statisticsIndex,2) = mean( sum(abs(vecH_realizations - H_hat).^2,1) ); %使用蒙特卡洛仿真来计算MSE
        
        
        %MVY估计法: 最优均匀训练功率分配
        P_training = diag(sqrt(q_uniform(:,k))); %均匀功率分配
        P_tilde = kron(transpose(P_training),eye(Nr));  %计算有效训练矩阵
        P_tilde_pseudoInverse = kron((P_training'/(P_training*P_training'))',eye(Nr)); %计算有效训练矩阵的伪逆
        
        average_MSE_MVU_estimator(k,statisticsIndex,1) = Nt^2*Nr/totalTrainingPower(k); %计算MSE
        
        H_hat = P_tilde_pseudoInverse'*(P_tilde*vecH_realizations + vecN_realizations); %使用蒙特卡洛仿真来计算该估计
        average_MSE_MVU_estimator(k,statisticsIndex,2) = mean( sum(abs(vecH_realizations - H_hat).^2,1) ); %使用蒙特卡洛仿真来计算MSE
        
        
        %One-sided linear 估计法: 最优训练功率分配又被称为 "LMMSE 估计法" 
       
        
        P_training = diag(sqrt(q_MMSE_heuristic(:,k))); %使用最优功率分配来计算训练矩阵 
        P_tilde = kron(P_training,eye(Nr)); %计算有效训练矩阵
        
        average_MSE_onesided_estimator(k,statisticsIndex,1) = trace(inv(inv(R_T)+P_training*P_training'/Nr)); %计算MSE
        
        Ao = (P_training'*R_T*P_training + Nr*eye(Nt))\P_training'*R_T; %计算one-sided linear估计法中的矩阵A0 
        H_hat = kron(transpose(Ao),eye(Nr))*(P_tilde*vecH_realizations + vecN_realizations); %使用蒙特卡洛仿真来计算该估计
        average_MSE_onesided_estimator(k,statisticsIndex,2) = mean( sum(abs(vecH_realizations - H_hat).^2,1) );  %使用蒙特卡洛仿真来计算MS
        
        
        %Two-sided linear 估计法: 最优训练功率分配
        
        P_training = diag(sqrt(q_uniform(:,k))); %计算训练矩阵，均匀功率分配
        P_tilde = kron(P_training,eye(Nr)); %计算有效训练矩阵
        R_calE = sum(1./q_uniform(:,k))*eye(Nr); %计算协方差矩阵
        
        average_MSE_twosided_estimator(k,statisticsIndex,1) = trace(R_R-(R_R/(R_R+R_calE))*R_R); %计算MSE
        
        C1 = inv(P_training); %计算矩阵C1
        C2bar = R_R/(R_R+R_calE); %计算C2bar矩阵
        H_hat = kron(transpose(C1),C2bar)*(P_tilde*vecH_realizations + vecN_realizations);
        average_MSE_twosided_estimator(k,statisticsIndex,2) = mean( sum(abs(vecH_realizations - H_hat).^2,1) ); %使用蒙特卡洛仿真来计算MS
        
    end
    
end


%挑选训练功率的子集
subset = linspace(1,length(totalTrainingPower_dB),5);

normalizationFactor = Nt*Nr; %设定MSE标准化因子为trace(R), 标准化MSE为从0到1.


%使用理论MSE公式画图
figure(1); hold on; box on;

plot(totalTrainingPower_dB,mean(average_MSE_MVU_estimator(:,:,1),2)/normalizationFactor,'b:','LineWidth',2);

plot(totalTrainingPower_dB,mean(average_MSE_twosided_estimator(:,:,1),2)/normalizationFactor,'k-.','LineWidth',1);
plot(totalTrainingPower_dB,mean(average_MSE_onesided_estimator(:,:,1),2)/normalizationFactor,'r-','LineWidth',1);

plot(totalTrainingPower_dB(subset(1)),mean(average_MSE_MMSE_estimator_heuristic(subset(1),:,1),2)/normalizationFactor,'b+-.','LineWidth',1);
plot(totalTrainingPower_dB(subset(1)),mean(average_MSE_MMSE_estimator_optimal(subset(1),:,1),2)/normalizationFactor,'ko-','LineWidth',1);

legend('MVU, optimal','Two-sided linear, optimal','One-sided linear, optimal','MMSE, heuristic','MMSE, optimal','Location','SouthWest')

plot(totalTrainingPower_dB,mean(average_MSE_MMSE_estimator_heuristic(:,:,1),2)/normalizationFactor,'b-.','LineWidth',1);
plot(totalTrainingPower_dB,mean(average_MSE_MMSE_estimator_optimal(:,:,1),2)/normalizationFactor,'k-','LineWidth',1);
plot(totalTrainingPower_dB(subset),mean(average_MSE_MMSE_estimator_heuristic(subset,:,1),2)/normalizationFactor,'b+','LineWidth',1);
plot(totalTrainingPower_dB(subset),mean(average_MSE_MMSE_estimator_optimal(subset,:,1),2)/normalizationFactor,'ko','LineWidth',1);


set(gca,'YScale','Log'); %纵轴为log范围
xlabel('Total Training Power (dB)');
ylabel('Average Normalized MSE');
axis([0 totalTrainingPower_dB(end) 0.05 1]);

title('Results based on theoretical formulas');


%使用蒙特卡洛仿真画理论运算图
figure(2); hold on; box on;

plot(totalTrainingPower_dB,mean(average_MSE_MVU_estimator(:,:,2),2)/normalizationFactor,'b:','LineWidth',2);
plot(totalTrainingPower_dB,mean(average_MSE_twosided_estimator(:,:,2),2)/normalizationFactor,'k-.','LineWidth',1);
plot(totalTrainingPower_dB,mean(average_MSE_onesided_estimator(:,:,2),2)/normalizationFactor,'r-','LineWidth',1);
plot(totalTrainingPower_dB(subset(1)),mean(average_MSE_MMSE_estimator_heuristic(subset(1),:,2),2)/normalizationFactor,'b+-.','LineWidth',1);
plot(totalTrainingPower_dB(subset(1)),mean(average_MSE_MMSE_estimator_optimal(subset(1),:,2),2)/normalizationFactor,'ko-','LineWidth',1);

legend('MVU, optimal','Two-sided linear, optimal','One-sided linear, optimal','MMSE, heuristic','MMSE, optimal','Location','SouthWest')

plot(totalTrainingPower_dB,mean(average_MSE_MMSE_estimator_heuristic(:,:,2),2)/normalizationFactor,'b-.','LineWidth',1);
plot(totalTrainingPower_dB,mean(average_MSE_MMSE_estimator_optimal(:,:,2),2)/normalizationFactor,'k-','LineWidth',1);
plot(totalTrainingPower_dB(subset),mean(average_MSE_MMSE_estimator_heuristic(subset,:,2),2)/normalizationFactor,'b+','LineWidth',1);
plot(totalTrainingPower_dB(subset),mean(average_MSE_MMSE_estimator_optimal(subset,:,2),2)/normalizationFactor,'ko','LineWidth',1);


set(gca,'YScale','Log'); %纵轴为log范围
xlabel('Total Training Power (dB)');
ylabel('Average Normalized MSE');
axis([0 totalTrainingPower_dB(end) 0.05 1]);

title('Results based on Monte-Carlo simulations');

包含每行具体代码的解释

（2）三个函数文件

function [deviation,powerAllocation]=functionLagrangeMultiplier(eigenvaluesTransmitter,totalPower,k,alpha)
%Compute the MSE for estimation of the squared Frobenius norm of the
%channel matrix for a given training power allocation. 
%INPUT:
%eigenvaluesTransmitter = Vector with the active eigenvalues at the
%                         transmitter side
%totalPower             = Total power of the training sequence
%k                      = Vector with k parameter values 
%alpha                  = Langrange multiplier value
%
%OUTPUT:
%deviation              = Difference between available power and used power
%powerAllocation        = Training power allocation 
%Compute power allocation 
powerAllocation = sqrt(8*(1./alpha(:))*eigenvaluesTransmitter'/3).*cos(repmat((-1).^k*pi/3,[length(alpha) 1])-atan(sqrt(8*(1./alpha(:))*(eigenvaluesTransmitter.^3)'/27-1))/3)-repmat(1./eigenvaluesTransmitter',[length(alpha) 1]);

%Deviation between total available power and the power that is used
deviation = abs(totalPower-sum(powerAllocation,2));

function MSE = functionMSEmatrix(R_diag,q_powerallocation,B)
%Compute the MSE for estimation of the channel matrix for a given training
%power allocation. 
%INPUT:
%R_diag            = Nt Nr x Nt Nr diagonal covariance matrix
%q_powerallocation = Nt x 1 vector with training power allocation
%B                 = Length of the training sequence.
%
%OUTPUT:
%MSE               = Mean Squared Error for estimation of the channel matrix

P_tilde = kron(diag(sqrt(q_powerallocation)),eye(B));

MSE = trace(R_diag - R_diag*(P_tilde'/(P_tilde*R_diag*P_tilde'+eye(length(R_diag))))*P_tilde*R_diag);

function MSE = functionMSEnorm(eigenvaluesTransmitter,eigenvaluesReceiver,powerAllocation)
%Compute the MSE for estimation of the squared Frobenius norm of the
%channel matrix for a given training power allocation. 
%INPUT:
%eigenvaluesTransmitter = Nt x 1 vector with eigenvalues at the
%                         transmitter side
%eigenvaluesReceiver    = Nr x 1 vector with eigenvalues at the
%                         receiver side
%powerAllocation        = Nt x 1 vector with training power allocation
%
%OUTPUT:
%MSE               = Mean Squared Error for estimation of the squared norm

MSE = sum(sum(((eigenvaluesTransmitter*eigenvaluesReceiver').^2 + 2*(powerAllocation.*eigenvaluesTransmitter.^3)*(eigenvaluesReceiver').^3)./(1+(powerAllocation.*eigenvaluesTransmitter)*eigenvaluesReceiver').^2));

注意：

• 此MIMO发射天线为8，接收天线为4；
• 三个函数文件的命名需要与函数保持一致；
• 先运行函数文件，再运行main主文件；
• 函数文件出现变量数报错是正常现象；
• 运行出来有两个图，选择任意一个图即可。

三. 运行结果与分析

分析：

3.1 均方误差（MSE）与训练功率（dB）的关系

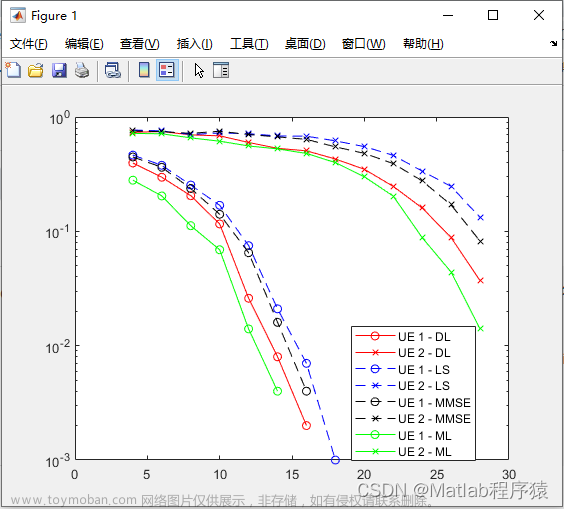
从图像上看，不管是何种信道估计方法，当训练功率增加时，均方误差（MSE）在减小。

MSE: Mean Square Error 均方误差

均方误差的全称为  误差平方的均值，误差也就是真实的信道值减去估计的信道值，我相信从名字来看就很好理解了，现在给出它的标准式子：

上式中E{}代表求里面的均值（数学期望），H代表信道准确值，代表信道估计值。

信道估计需要发送导频信号，训练功率越大证明投入的越多，信道估计的误差也就越小，信道估计性能越好，均方误差也就越小，这也就是解释了为什么所有的曲线均呈现递减的趋势。

3.2 不同信道估计方法性能对比

纵向对比，信道估计从最优到最劣分别为：MMSE（optimal），MMSE(heuristic)，one-sided linear，two-side linear，MVU。

本图一共展现了五种MIMO信道估计的方法，要想搞清楚图形如此，就需要分析每一种信道估计方法。

（1）MVU,optimal

先从最差的开始。MVU全称 minimum variance unbiased 中文翻译为最小方差无偏。文章来源地址https://www.toymoban.com/news/detail-460775.html

到了这里，关于基于MATLAB的MIMO信道估计（附完整代码与分析）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！