数学建模学习笔记（一）:插值法-Toy模板网

这篇具有很好参考价值的文章主要介绍了数学建模学习笔记（一）:插值法。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

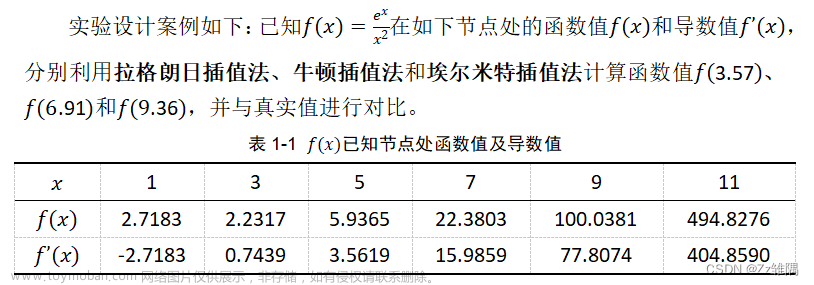
前言

本文主要内容是分享博主在学习MATLAB插值与拟合过程中的一些笔记与见解，并记录使用代码实现的过程

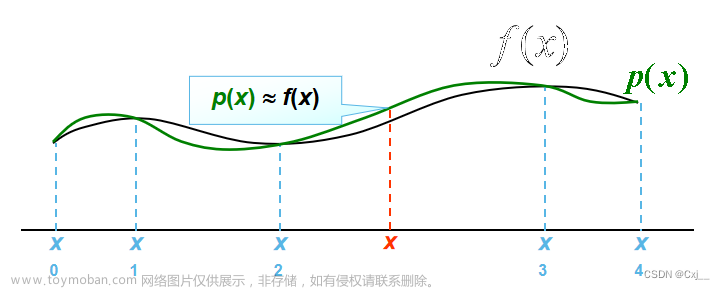
一、一维插值问题的描述

一维插值问题可描述为：已知函数在 $x_0,x_1,…,x_n$ 处的值 $y_0,y_1,…,y_n$ ,求简单函数 $p (x)$ ,使 $p(x_i)=y_i.$
通俗来说，即已知函数在某区间内若干点处的值，求函数在该区间内其他点处的值。
PS：这里可以用范德蒙行列式和克莱姆法则证明，在 $x_0,x_1,…,x_n$ 处取值为 $y_0,y_1,…,y_n$ 的多项式存在且唯一，即插值问题的解唯一存在。（相关内容见线性代数）

二、常用插值方法

1.Lagrange插值法

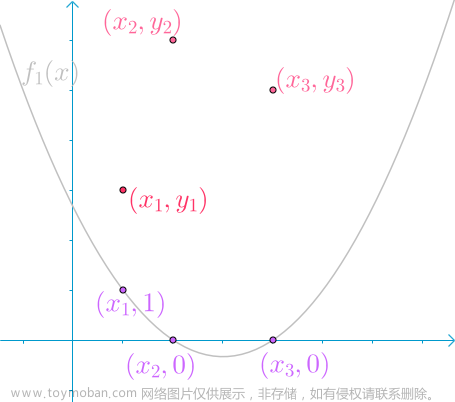
Lagrange(拉格朗日)插值公式，指的是在节点上给出节点基函数，然后做基函数的线性拟合，组合系数为节点函数值的一种插值多项式。
假设，我们已知函数 $f (x)$ 在平面坐标系上有3个点，坐标分别为 $x_1,y_1)$ , $x_2,y_2)$ , $x_3,y_3)$ ，可以分别根据这三个点找出节点基函数。例如，首先作出基函数 $f_1$ 的图像，经过 $x_1,1)$ , $x_2,0)$ , $x_3,0)$ 这三个点，同理可作出 $f_2$ 分别经过点 $x_1,0)$ , $x_2,1)$ , $x_3,0)$ 以及 $f_3$ 。通过寻找这三组基函数的线性组合，我们不难发现原函数可以写出如下形式：
$f(x)=y_1f_1(x)+y_2f_2(x)+y_3f_3(x)$ 上式可推广为: $f(x)=\sum_{i=0}^{k}{y_i\prod_{j\ne1}\frac {x-x_j} {x_i-x_j}}$ Lagrange插值多项式结构紧凑，在理论分析中甚为方便，但是其缺点在于当插值节点增减时，全部插值基函数均要随之变化，整个公式也将发生变化，在实际计算中很不方便。

2.Newton插值法

Newton（牛顿）插值法相对于拉格朗日插值法具有承袭性的优势，即在增加额外的插值点时，可以利用之前的运算结果以降低运算量。
假设已知n+1个点相对多项式函数 $f f$ 的值为： $x_0,f(x_0)),(x_1,f(x_1)),(x_2,f(x_2)),⋯,(x_n,f(x_n))$ ，求此多项式函数 $f$ .
先从求满足两个点 $x_0,f(x_0)),(x_1,f(x_1))$ 的函数 $f_1(x)$ 说起：
假设 $f_1(x)=f(x_0)+b_1(x−x_0)$ ，
我们增加一个点， $x_0,f(x_0)),(x_1,f(x_1)),(x_2,f(x_2))$ ，求满足这三个点的函数 $f_2(x)$ :
假设 $f_2(x)=f_1(x)+b_2(x−x_0)(x−x_1$ )，
以此类推，我们得到Newton插值法的函数为：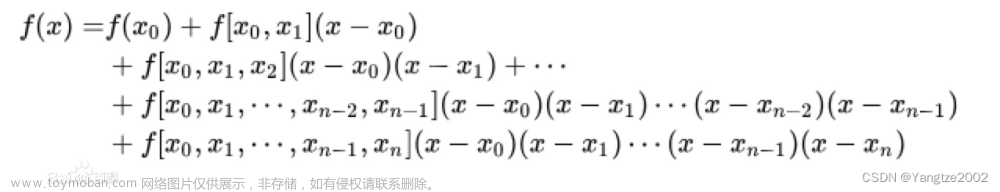
百度百科
其优点在于：每增加一个点，不会导致之前的重新计算，只需要算和新增点有关的就可以了。

三、高次插值的Runge现象

在研究插值问题的初期，所有人都想当然地认为插值多项式的次数越高，插值精度越高。
Runge通过研究发现有的情况下，并非插值多项式阶数越高结果就越精确。当插值多项式的次数较高时，结果会出现严重的振荡现象，称之为Runge现象。
例如，我们在均匀节点上对Runge函数
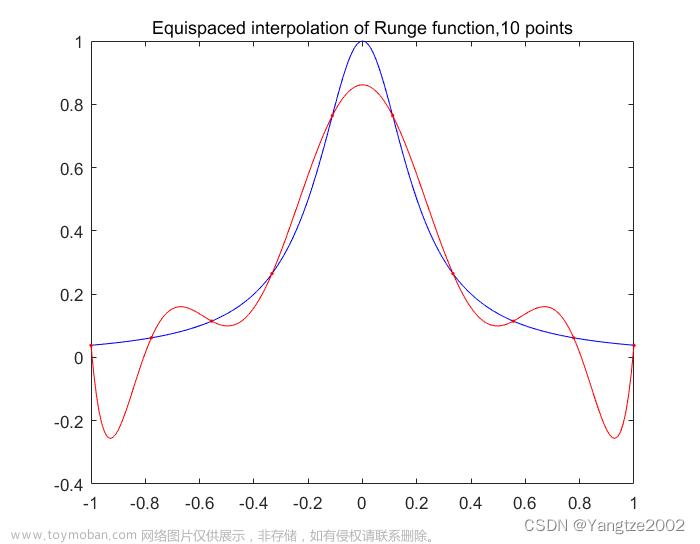$f(x)=\frac{1}{1+25x^2},x\in[-1,1]$ 进行插值，（如图）数学建模学习笔记（一）:插值法红色曲线代表插值多项式的阶数为10时呈现的效果，可以看出，插值区间的边缘产生了严重的振荡现象，误差很大。因此，在实际中应避免使用高次的插值。通常为避免Runge现象，我们可以将插值区间分成若干小区间，在小区间内用低次插值，即分段低次插值，如样条函数插值。

四、Matlab插值

1、一维插值

当一组数据可以表示成平面坐标系上的点时，我们可以使用Matlab的一维插值命令:

yi=inter1(x,y,xi,'method')
%x,y为插值点，xi,yi为被插值点和结果，x,y和xi,yi通常为向量
%'method'表示插值方法：常用方法有'nearest''linear''spline''cubic'

‘nearest’——最邻近插值:插入与其距离最近的值
‘linear’——线性插值：构造线性函数进行插值
‘spline’——三次样条插值：将定义域分成若干个区间，在每个区间内构造三次多项式进行插值
‘cubic’——立方插值：构造立方函数进行插值
ps:'method’缺省时默认为线性插值

2、二维插值

当一组数据可以表示成空间坐标系上的点时，我们可以使用Matlab的二维插值命令:

yi=inter2(x,y,z,xi,yi,'method')
%x,y,z为插值点，xi,yi为被插值点,zi为输出的插值结果，即插值函数在（xi,yi）处的值；x,y为向量，xi,yi为向量或矩阵，而z和zi则为矩阵
%'method'表示插值方法：常用方法有'nearest''linear''spline''cubic'

‘nearest’——最邻近插值:插入与其距离最近的值
‘linear’——双线性插值：构造两组线性函数进行插值
‘spline’——双三次样条插值：将定义域分成若干个区间，在每个区间内构造三次多项式进行插值
‘cubic’——双立方插值：构造立方函数进行插值
默认为双线性插值

3、散乱点插值

当插值点（x,y）为散乱点，不再是网格上的点时，可以使用griddata命令进行二维插值：

griddata(x,y,z,xi,yi,'method')%'method'用法同上

总结

本文主要展示了数学建模中的一些插值方法及原理，并且基于Matlab进行实现的过程。由于作者也是在学习阶段，此篇文章仅供参考，欢迎大家指正！

参考资料

[1]【【零基础教程】老哥：数学建模算法、编程、写作和获奖指南全流程培训！】 https://www.bilibili.com/video/BV1kC4y1a7Ee?p=24&share_source=copy_web&vd_source=c62a50333f8ab9149f6acfdf0a7c31e7

[2]https://baike.baidu.com/item/%E7%89%9B%E9%A1%BF%E6%8F%92%E5%80%BC%E6%B3%95/7085983

[3]https://zhuanlan.zhihu.com/p/138747068文章来源地址https://www.toymoban.com/news/detail-461354.html

到了这里，关于数学建模学习笔记（一）:插值法的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！