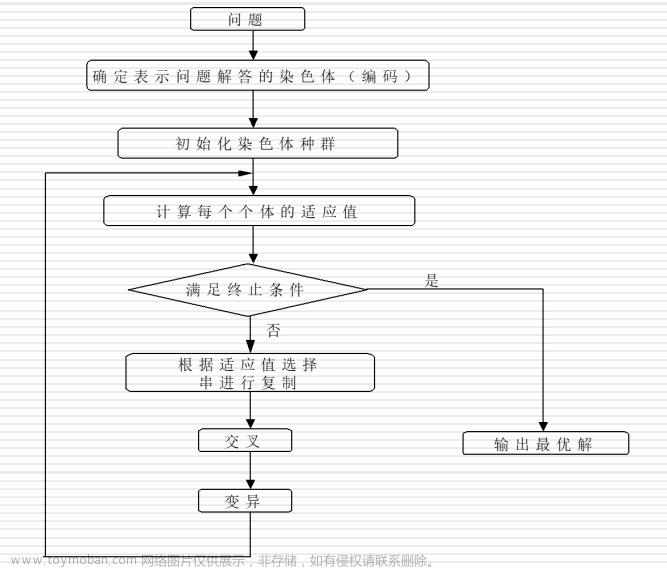
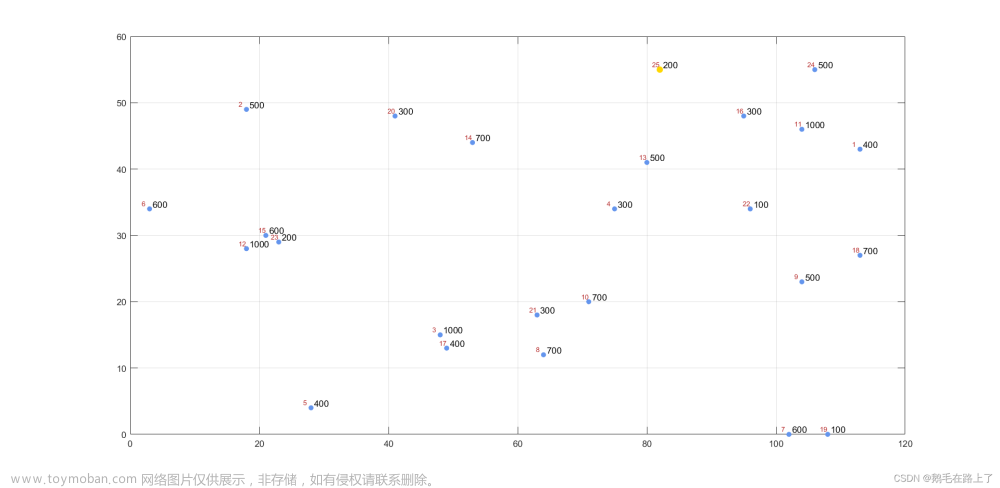
回溯问题适合于解由向量的形式来构成的，这个向量空间中使用搜索的方法进行搜索，搜索使用宽度优先的方法。货郎问题又名旅行商问题，但其实更多教科书中更通用的叫法叫旅行商问题，下面来对旅行商问题使用回溯算法证明。
一、问题描述
有n个城市，已知任两个城市之间的距离，求一条每个城市恰好经过一次的回路，使得总长度最小 。
分析：
有n个城市，城市与城市之前有距离的，任意两个城市之间的距离是已知的，现在需要找一条回路，经过每一个城市1次，使得总长度最小，就相当于这个货郎在路途，或者旅行商的行路，遍历所有的城市去各个城市走一趟，但是城市不能重复，所以怎么走下来才能够使得总长度达到最小。
其实相当于把这些城市做一个排列，第一个城市指向k1所指向的城市，由城市k1走向城市k2，一直往下走，走到kn以后再回到k1形成一个闭环
二、数学建模
数学表达式中的C k1到C k2，这两个城市的距离用d来表示，走到最后一个城市再倒回来(从C kn到C k1)，这个距离达到最小，就是我们要做的事情。
这个问题是有选择的，一定程度上讲，TSP也是优化问题，只要是涉及到有选择，选择的不同导致结果的不同，结果的不同要想法设法找出最好的选择，不管是调度问题、背包的装法问题还是这个城市排列的问题，现代的智能优化算法不再使用精确的解，而是找到一个近似最精确的解就可以了。
三、实例
1、传统经典做法
从第1个城市走到第2个城市，从第2个城市走到第4个城市，从第4个城市到第3个城市然后再回来。
C={1,2,3,4}
d(1,2)=5, d(1,3)=9,
d(1,4)=4, d(2,3)=13,
d(2,4)=2, d(3,4)=7
解：< 1,2,4,3 > ,
长度= 5 + 2 + 7 + 9 = 23
这是其中一个解，最后的解得到的是城市的排列向量，上面原始的数据每两个城市之间的距离都是给出的。
2、回溯算法
假定每个城市都有连接，回溯算法的实现也是一种搜索，首先对于第一个城市出发，第1个城市和2，3，4城市相连，这个时候做选择，选择任何一条路径往下走，走到第2个城市，又有两种选择：到第4个城市，或者到第3个城市。每走到一个城市就选相当于前面已经走过的城市就不用再选择了，就从剩下的城市中去选。
一开始选定任何一个出发点出发，接下来又n-1个城市可以去选择，当你走到任何一个点之后，接下来又有n-2个城市可以去选择，……一直到最后只有1种选择，就是唯一的选择：回去。所以总的路径有(n-1)!种，每到叶结点的路径就是城市间的路径。
表示为树，称之为排列树，有(n-1)!片树叶
其实我们要找的就是在所有的排列树叶结点中去找最小的那个，所以搜索空间是相当大的。文章来源：https://www.toymoban.com/news/detail-461482.html
文章来源地址https://www.toymoban.com/news/detail-461482.html
四、总结
- 解：向量
- 搜索空间：树，可能是n叉树、子集树、排列树等等，树的结点对应于部分向量，可行解在叶结点
- 搜索方法：深度优先, 宽度优先, …
跳越式遍历搜索树，找到解
到了这里，关于旅行商问题（回溯算法）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
