页面置换算法（OPT、FIFO、LRU、时钟、LFU）-Toy模板网

这篇具有很好参考价值的文章主要介绍了页面置换算法（OPT、FIFO、LRU、时钟、LFU）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

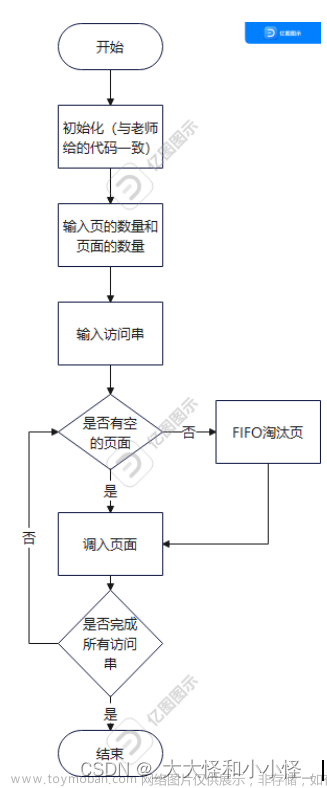
前言

在地址映射过程中，若在页面中发现所要访问的页面不在内存中，则产生缺页中断。当发生缺页中断时，如果操作系统内存中没有空闲页面，则操作系统必须在内存选择一个页面将其移出内存，以便为即将调入的页面让出空间。而用来选择淘汰哪一页的规则叫做页面置换算法。

一、缺页中断

在说内存页面置换算法前，我们得先谈⼀下缺页异常（缺页中断）。当 CPU 访问的页面不在物理内存时，便会产生一个缺页中断，请求操作系统将所缺页调入到物理内存。

如果在这个过程中，物理内存找不到空闲页，就需要页面置换算法，选择⼀个物理页面换出到磁盘，然后把需要访问的页面换入到物理。

页面置换算法的目标是：尽可能减少页面的换入换出的次数。

二、最佳页面置换算法（OPT）

最佳⻚⾯置换算法基本思路是，置换在「未来」最长时间不访问的页面

这很理想，但是实际系统中无法实现，因为程序访问页面时是动态的，我们是无法预知每个页面在「下⼀次」访问前的等待时间。

所以，最佳页面置换算法作用是为了衡量你的算法的效率，你的算法效率越接近该算法的效率，那么说明你的算法是⾼效的

三、先进先出置换算法（FIFO）

既然我们⽆法预知⻚⾯在下⼀次访问前所需的等待时间，那我们可以选择在内存驻留时间很长的页面进行中置换，这个就是先进先出置换算法的思想。

缺点：跟最佳页面置换算法比较起来，性能明显差了很多。

四、最近最久未使用的置换算法（LRU）

最近最久未使⽤（LRU）的置换算法的基本思路是，发⽣缺页时，选择最长时间没有被访问的页面进行置换，也就是说，该算法假设已经很久没有使用的页面很有可能在未来较长的⼀段时间内仍然不会被使用。

这种算法近似最优置换算法，最优置换算法是通过未来的使⽤情况来推测要淘汰的⻚⾯，而 LRU 则是通过历史的使用情况来推测要淘汰的页面，其置换页面的流程如下所示：
页面置换算法（OPT、FIFO、LRU、时钟、LFU）

虽然 LRU 在理论上是可以实现的，但代价很高。为了完全实现 LRU，需要在内存中维护⼀个所有页面的链表，最近最多使用的页面在表头，最近最少使用的页面在表尾。

困难的是，在每次访问内存时都必须要更新「整个链表」。在链表中找到⼀个页面，删除它，然后把它移动到表头是⼀个⾮常费时的操作。

所以，LRU 虽然看上去不错，但是由于开销比较大，实际应用中比较少使用。

五、时钟页面置换算法

那有没有⼀种即能优化置换的次数，也能方便实现的算法呢？
答：时钟页面置换算法就可以两者兼得，它跟 LRU 近似，⼜是对 FIFO 的⼀种改进。

该算法的思路是，把所有的页面都保存在⼀个类似钟面的「环形链表」中，⼀个表针指向最老的页面。

当缺页中断时，算法首先检查表针指向的页面：

1、如果它的访问位位是 0 就淘汰该页面，并把新的页面插入这个位置，然后把表针前移⼀个位置。

2、如果访问位是 1 就清除访问位，并把表针前移⼀个位置，重复这个过程直到找到了⼀个访问位为 0 的页面为⽌。

六、最不常用置换算法（LFU）

⽽是当发生缺页中断时，选择访问次数最少的那个页面，并将其淘汰。

它的实现方式是，对每个页面设置⼀个访问计数器，每当⼀个页面被访问时，该页⾯的访问计数器就累加 1。在发生缺页中断时，淘汰计数器值最小的那个页面。

但还有个问题，LFU 算法只考虑了频率问题，没考虑时间的问题，比如有些页面在过去时间里访问的频率很高，但是现在已经没有访问了，而当前频繁访问的页面由于没有这些页面访问的次数高，在发生缺页中断时，就会可能会误伤当前刚开始频繁访问，但访问次数还不高的页面。

七、如果要你自己实现一个LRU调度算法你怎么做？

1.首先要接收一个 capacity 参数作为缓存的最大容量，然后实现两个 API，一个是 put(key, val) 方法存入键值对，另一个是 get(key) 方法获取 key 对应的 val，如果 key 不存在则返回 -1。

/* 缓存容量为 2 */
LRUCache cache = new LRUCache(2);
// 你可以把 cache 理解成一个队列
// 假设左边是队头，右边是队尾
// 最近使用的排在队头，久未使用的排在队尾
// 圆括号表示键值对 (key, val)

cache.put(1, 1);
// cache = [(1, 1)]

cache.put(2, 2);
// cache = [(2, 2), (1, 1)]

cache.get(1);       // 返回 1
// cache = [(1, 1), (2, 2)]
// 解释：因为最近访问了键 1，所以提前至队头
// 返回键 1 对应的值 1

cache.put(3, 3);
// cache = [(3, 3), (1, 1)]
// 解释：缓存容量已满，需要删除内容空出位置
// 优先删除久未使用的数据，也就是队尾的数据
// 然后把新的数据插入队头

cache.get(2);       // 返回 -1 (未找到)
// cache = [(3, 3), (1, 1)]
// 解释：cache 中不存在键为 2 的数据

cache.put(1, 4);    
// cache = [(1, 4), (3, 3)]
// 解释：键 1 已存在，把原始值 1 覆盖为 4
// 不要忘了也要将键值对提前到队头

分析上面的操作过程，要让 put 和 get 方法的时间复杂度为 O(1)，我们可以总结出 cache 这个数据结构必要的条件：

1、显然 cache 中的元素必须有时序，以区分最近使用的和久未使用的数据，当容量满了之后要删除最久未使用的那个元素腾位置。

2、我们要在 cache 中快速找某个 key 是否已存在并得到对应的 val；

3、每次访问 cache 中的某个 key，需要将这个元素变为最近使用的，也就是说 cache 要支持在任意位置快速插入和删除元素。

那么，什么数据结构同时符合上述条件呢？哈希表查找快，但是数据无固定顺序；链表有顺序之分，插入删除快，但是查找慢。所以结合一下，形成一种新的数据结构：哈希链表 LinkedHashMap。

LRU 缓存算法的核心数据结构就是哈希链表，双向链表和哈希表的结合体。在做的时候可以自己实现双向链表和哈希表，或者Java 内置的 LinkedHashMap就是这种结构，都是可以实现的。
页面置换算法（OPT、FIFO、LRU、时钟、LFU）

为什么用双向链表？

删除一个节点不光要得到该节点本身的指针，也需要操作其前驱节点的指针，而双向链表才能支持直接查找前驱，保证操作的时间复杂度 O(1)。

为什么要在链表中同时存储 key 和 val，而不是只存储 val？

也就是说，当缓存容量已满，我们不仅仅要删除最后一个 Node 节点，还要把 map 中映射到该节点的 key 同时删除，而这个 key 只能由 Node 得到。如果 Node 结构中只存储 val，那么我们就无法得知 key 是什么，就无法删除 map 中的键，造成错误。

借助这个结构，我们来逐一分析上面的 3 个条件：

1、如果我们每次默认从链表尾部添加元素，那么显然越靠尾部的元素就是最近使用的，越靠头部的元素就是最久未使用的。

2、对于某一个 key，我们可以通过哈希表快速定位到链表中的节点，从而取得对应 val。

3、链表显然是支持在任意位置快速插入和删除的，改改指针就行。只不过传统的链表无法按照索引快速访问某一个位置的元素，而这里借助哈希表，可以通过 key 快速映射到任意一个链表节点，然后进行插入和删除。

LinkedHashMap实现LRU页面调度算法的JAVA代码如下所示：

class LRUCache {
    int cap;
    LinkedHashMap<Integer, Integer> cache = new LinkedHashMap<>();
    public LRUCache(int capacity) { 
        this.cap = capacity;
    }
    
    public int get(int key) {
        if (!cache.containsKey(key)) {
            return -1;
        }
        // 将 key 变为最近使用
        makeRecently(key);
        return cache.get(key);
    }
    
    public void put(int key, int val) {
        if (cache.containsKey(key)) {
            // 修改 key 的值
            cache.put(key, val);
            // 将 key 变为最近使用
            makeRecently(key);
            return;
        }
        
        if (cache.size() >= this.cap) {
            // 链表头部就是最久未使用的 key
            int oldestKey = cache.keySet().iterator().next();
            cache.remove(oldestKey);
        }
        // 将新的 key 添加链表尾部
        cache.put(key, val);
    }
    
    private void makeRecently(int key) {
        int val = cache.get(key);
        // 删除 key，重新插入到队尾
        cache.remove(key);
        cache.put(key, val);
    }
}